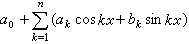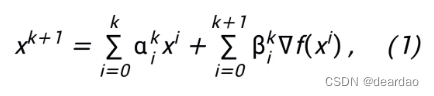逼近专题
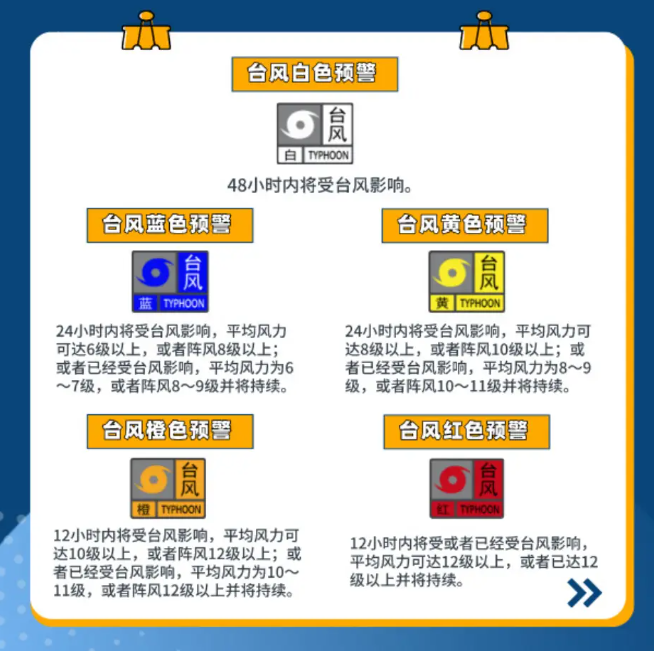
超强台风摩羯逼近!或成大陆史上最强登陆台风,防御措施需到位
超强台风摩羯逼近!或成大陆史上最强登陆台风,防御措施需到位 摩羯即将登录,各位兄弟姐妹注意安全!#大型纪录片#摩羯#台风 推荐阅读: 一夜蒸发2万亿!英伟达市值遭遇滑铁卢 《火速围观!黑神话悟空IP山西空心月饼,又一波抢购热潮即将来袭》 直击心灵!佤写不来情歌,却意外火爆全网,你听了没? 警告!明年6至9月假期空窗期,你的旅行计划何去何从? 独家揭秘!雷军豪赠《黑神话:悟空》给王腾,
【凸优化】连续凸逼近
文章目录 1-理论2-实践 1-理论 连续凸逼近(Successive Convex Approximation, SCA)是一种用于解决非凸优化问题的常用方法。它通过将原始非凸问题分解为一系列凸子问题来求解,每个子问题都是在上一步的解的基础上构造的,逐步逼近全局最优解。以下是连续凸逼近的一般求解过程: 问题描述 设有一个非凸优化问题,其形式如下: min x f
从函数逼近角度理解神经网络、残差连接与激活函数
概述 最近思考激活函数的时候,突然想到神经网络中残差连接是不是和函数的泰勒展开很像,尤其是在激活函数 f ( x ) = x 2 f(x)=x^2 f(x)=x2时(这个激活函数想法来源于 f ( x ) = R e L U 2 ( x ) [ 3 ] f(x)=ReLU^2(x)[3] f(x)=ReLU2(x)[3]),所以验证了一下就顺便写下来了,本文抛砖引玉,如果有建议或更好的想法可以写
OpenCV轮廓、多边形逼近、关键点、周长和面积、边界框、矩、轮廓树、凹凸包、几何直方图、匹配
1.轮廓的多边形逼近 2.轮廓的关键点 3.轮廓的周长和面积 4.轮廓的边界框 5.轮廓的矩 6.轮廓的轮廓树 7.轮廓的凸包和凸缺陷 8.轮廓的成对几何直方图 9.轮廓的匹配 轮廓的特性: 1.轮廓的多边形逼近 轮廓的多边形逼近指的是:使用多边形来近似表示一个轮廓。 多边形逼近的目的是为了减少轮
浪潮信息打造业界首款50℃进液温度服务器 PUE逼近理论极限1.0!
在科技飞速发展的今天,浪潮信息以其前瞻性的技术创新思维,再次突破行业极限,推出业界首个支持50℃进液温度的浸没式液冷服务器NF5180G7。这一创新成果不仅展现了浪潮信息在液冷技术领域的深厚实力,更标志着服务器冷却技术的一次重大飞跃。 NF5180G7是一款超高密度服务器,在1U空间内达到了性能、密度、扩展性最大化设计,支持2颗最高64核心350W最新英特尔至强可扩展处理器,最大支持32个DDR
给定函数的Chebyshev逼近
//计算给定函数的Chebyshev逼近 #include <iostream> #include <math.h> #include <fstream> #include <iomanip> using namespace std; const double pi = 3.141592653589793; class chebyshev { private: int div, i, j,
设计普遍逼近的深度神经网络:一阶优化方法
论文地址:https://ieeexplore.ieee.org/document/10477580 传统的基于优化的神经网络设计方法通常从一个具有显式表示的目标函数出发,采用特定的优化算法进行求解,再将优化迭代格式映射为神经网络架构,例如著名的 LISTA-NN 就是利用 LISTA 算法求解 LASSO 问题所得 [4],这种方法受限于目标函数的显式表达式,可设计得到的网络结构有限。一些研究
每天五分钟深度学习:如何理解梯度下降算法可以逼近全局最小值?
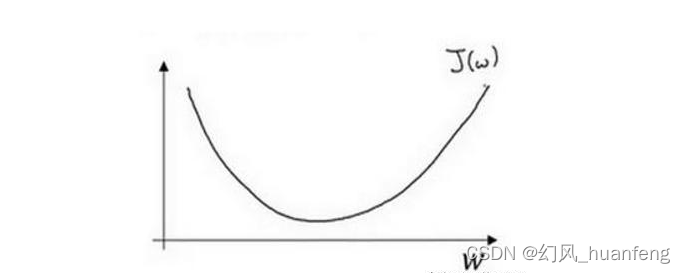
本文重点 上节课程中,我们已经知道了逻辑回归的代价函数J。要想最小化代价函数,我们需要使用梯度下降算法。 梯度下降算法地直观理解: 为了可视化,我们假设w和b都是单一实数,实际上,w可以是更高地维度。 代价函数J是在水平轴w和b上的曲面,因此曲面的高度就是J(w,b)在某一点(w,b)的函数值。我们要做的就是找到使得代价函数J最小的值所对应地w和b。 从逻辑回归的损失函数来看梯度下降
HalconLen5-定位特征步步逼近
read_image(Image, 'C:/Users/86173/Desktop/test/2.png')get_image_size(Image, Width, Height)dev_close_window()dev_open_window(0, 0, Width, Height, 'black', WindowHandle)dev_display(Image)threshold(Ima
数值分析复习:逼近理论的应用——最小二乘问题、解超定、欠定方程组
文章目录 逼近理论的应用——最小二乘问题、解超定、欠定方程组离散平方逼近最小二乘解 本篇文章适合个人复习翻阅,不建议新手入门使用 本专栏:数值分析复习 的前置知识主要有:数学分析、高等代数、泛函分析 逼近理论的应用——最小二乘问题、解超定、欠定方程组 离散平方逼近 设全空间 X = R n X=\mathbb{R}^n X=Rn, 在 R n \mathbb{R}
leetcode - 303. Range Sum Query - Immutable 【动态规划 + 间接逼近目标 + 区间计算 +刻度 + 距离计算方式 】
题目 Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive. Example: Given nums = [-2, 0, 3, -5, 2, -1]sumRange(0, 2) -> 1sumRange(2, 5) -> -1sumRa
切比雪夫逼近法设计FIR滤波器
切比雪夫逼近法设计FIR滤波器 概念 切比雪夫逼近法,是在所需要的区间[a,b]内,使误差函数E(x)=|p(x)-f(x)|较均匀一致,并且通过合理选择p(x),使E(x)的最大值En达到最小。切比雪夫最佳一致逼近的基本思想是,对于给定区间[a,b]上的连续函数f(x),在所有n次多项式的集合中,寻找一个多项式,使其在[a,b]上对f(x)的偏差和其他一切属于集合的多项式对f(x)的偏差相比
中国企业“战略迷失悲剧”逼近高发期--中国房地产企业即将迎来倒闭潮
“最后一根稻草”压垮中国房地产企业——已近在咫尺! 由于过度重视与地方政府关系,而过度轻视宏观战略预测,过分蔑视社会公众怨声,中国大部分房地产企业正将迎来严峻宏观调控和市场泡沫破灭的严厉惩罚——未来6-12个月,中国房企将会有相当比例破产倒闭。 房地产企业的最后一丝侥幸正变成绝望。2010年调控以来,银根收紧,房地产的企业信贷和个人房贷都急剧紧缩,股市融资也停顿下来。2011年以
L^2准则下的多项式逼近,一个比较有意思的问题吧
问题描述 实际上: f ( a ) = ∫ ( g − ∑ 0 n a i x i ) 2 = ∫ g 2 + ∫ ( ∑ 0 n a i x i ) 2 − 2 ∫ g ∑ 0 n a i x i f(a)=\int(g-\sum_0^na_ix^i)^2=\int g^2+\int (\sum_0^na_ix^i)^2-2\int g\sum_0^na_ix^i f(a)=∫(g−∑0na
比特币暴涨逼近历史最高点;阿里云全线降价20%丨 RTE 开发者日报 Vol.155
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE (Real Time Engagement) 领域内「有话题的 新闻 」、「有态度的 观点 」、「有意思的 数据 」、「有思考的 文章 」、「有看点的 会议 」,但内容仅代表编辑的个人观点,欢迎大家留言、跟帖、讨论。 本期编辑:@CY 01 有话题的新闻 1、阿里
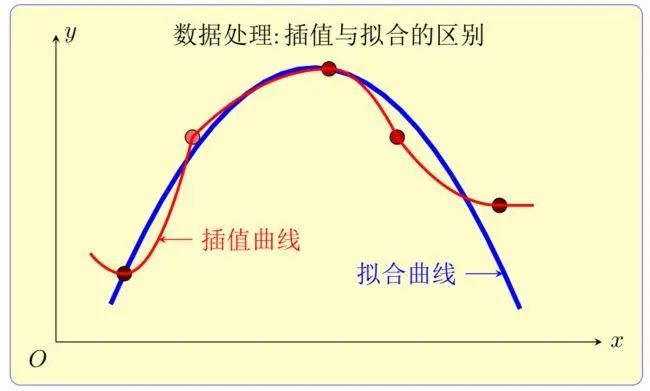
插值、逼近、拟合、光顺
插值 插值(Interpolation)是数学和计算科学中的一个重要概念,它指的是通过已知的一系列数据点,构造一个函数或曲线,并据此估计未知数据点的值。这个过程通常发生在已知数据点之间,用于预测或估算在这些已知点之间的某个位置的值。 插值有多种方法,包括线性插值、多项式插值、样条插值(如立方样条插值)、径向基函数插值等。选择哪种插值方法取决于具体的应用场景、数据点的分布、所需的精度和计算效率等
【RL】Value Function Approximation(值函数逼近)
Lecture 8: Value Function Approximation Algorithm for state value estimation Objective function 令 v π ( s ) v_{\pi}(s) vπ(s)和 v ^ ( s , w ) \hat{v}(s, w) v^(s,w)是真实state value和近似函数。 算法的目标是找到一个最优的
m基于万能逼近原理自适应模糊控制算法的多自由度AUV运动控制抗干扰补偿simulink仿真
目录 1.算法仿真效果 2.算法涉及理论知识概要 3.MATLAB核心程序 4.完整算法代码文件 1.算法仿真效果 matlab2022a仿真结果如下: 2.算法涉及理论知识概要 自主水下航行器(Autonomous Underwater Vehicle,AUV)是一种具有自主性、灵活性、隐蔽性等优点的智能化设备,广泛应用于
OpenCV-36 多边形逼近与凸包
目录 一、多边形的逼近 二、凸包 一、多边形的逼近 findContours后的轮廓信息countours可能过于复杂不平滑,可以用approxPolyDP函数对该多边形曲线做适当近似,这就是轮廓的多边形逼近。 apporxPolyDP就是以多边形去逼近轮廓,采用的是Douglas-Peucker算法(方法名中的DP) DP算法原理比较简单,核心就是不断去找多边形最远的点加入形
牛顿法,也称为牛顿-拉弗森方法,是一种迭代逼近的数值计算方法,可用于求解方程的根。牛顿法也可以用来求平方根。
牛顿法,也称为牛顿-拉弗森方法,是一种迭代逼近的数值计算方法,可用于求解方程的根。牛顿法也可以用来求平方根。 设要求解的数的平方根为x,则可以将问题转化为求方程f(x) = x^2 - n = 0的根,其中n为待求平方根的数。 牛顿法的迭代公式为: x_(k+1) = x_k - f(x_k) / f'(x_k) 其中,x_k表示第k次迭代的近似解,f'(x_k)表示f(x)在x_k处的
数值分析复习(四)——多项式插值与函数逼近
四、多项式插值与函数最佳逼近 设函数 y = f ( x ) y = f(x) y=f(x) 在区间 [ a , b ] [a, b] [a,b] 上有定义,且已知在点 a ≤ x 0 < x 1 < ⋯ < x n ≤ b a \le x_0 \lt x_1 \lt \cdots \lt x_n \le b a≤x0<x1<⋯<xn≤b 上的值 f ( x 0 ) , f ( x
董宇辉逼近小杨哥,但东方甄选跟得上吗?
随着“小作文风波”的结束,董宇辉和东方甄选的关系得到重构,个人IP价值打开了天花板,正在逼近粉丝意义上的“抖音一哥”疯狂小杨哥。 成立“与辉同行”直播间之后,董宇辉迅速积累粉丝过千万,1月 9日 的“单飞”首秀,一夜吸金1.5亿元,12日甚至因为“货买完了”而停播一天, 声势堪比当年李佳琦复出。单论粉丝购买力,董宇辉已经有超越疯狂小杨哥的苗头。首秀当晚,董宇辉单个粉丝平均贡献了 12.5元,而疯
带延迟的随机逼近方案(Stochastic approximation schemes):在网络和机器学习中的应用
1. 并行队列系统中的动态定价Dynamic pricing 1.1 系统的表述 一个含有并行队列的动态定价系统,该系统中对于每个队列有一个入口收费(entry charge) ,且系统运行的目标是保持队列长度接近于某个理想的配置。 这里是这个系统的几个关键假设: a. 存在 K 个并行队列(parallel queues):每个队列 i
牛顿迭代法、迭代逼近
/*zstu 求一元三次方程的根 要求1附近的根,只要把x0初始化为1代入,然后牛顿迭代1000次就出结果了 */ #include<stdio.h>double c[4],d[3];double f(double x){double fac=1,sum=0;int i;for(i=0;i<4;i++){sum+=fac*c[i];fac*=x;}return sum