本文主要是介绍函数逼近问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://baike.so.com/doc/6449832.html
函数论的一个重要组成部分,涉及的基本问题是函数的近似表示问题。在数学的理论研究和实际应用中经常遇到下类问题:在选定的一类函数中寻找某个函数g,使它是已知函数ƒ在一定意义下的近似表示,并求出用g近似表示 ƒ而产生的误差。这就是函数逼近问题。在函数逼近问题中,用来逼近已知函数ƒ的函数类可以有不同的选择;即使函数类选定了,在该类函数中用作ƒ的近似表示的函数g的确定方式仍然是各式各样的;g对ƒ的近似程度(误差)也可以有各种不同的含义。所以函数逼近问题的提法具有多样的形式,其内容十分丰富。
逼近函数类给定函数ƒ(x),用来逼近ƒ(x)的函数一般要在某个较简单的函数类中找,这种函数类叫做逼近函数类。逼近函数类可以有多种选择。n次代数多项式,亦即一切形如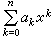 函数逼近论
函数逼近论
(其中α0,α1,…,αn是实数,k=0,1,…)的函数的集合;n阶三角多项式,亦即一切形如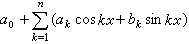 函数逼近论
函数逼近论
(其中α0,α1,…,αn,b1,b2,…,bn是实数,k=1,2,…)的函数的集合,这些是最常用的逼近函数类。其他如由代数多项式的比构成的有理分式集,由正交函数系的线性组合构成的(维数固定的)线性集,按照一定条件定义的样条函数集等也都是很有用的逼近函数类。在一个逼近问题中选择什么样的函数类作逼近函数类,这要取决于被逼近函数本身的特点,也和逼近问题的条件、要求等因素有关。
这篇关于函数逼近问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






