m基于万能逼近原理自适应模糊控制算法的多自由度AUV运动控制抗干扰补偿simulink仿真

2024-02-13 10:50
文章标签 算法 万能 仿真 原理 simulink 控制 适应 运动 逼近 自由度 补偿 模糊控制 抗干扰 auv

本文主要是介绍m基于万能逼近原理自适应模糊控制算法的多自由度AUV运动控制抗干扰补偿simulink仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

1.算法仿真效果

2.算法涉及理论知识概要

3.MATLAB核心程序

4.完整算法代码文件

1.算法仿真效果

matlab2022a仿真结果如下：

 

 

 

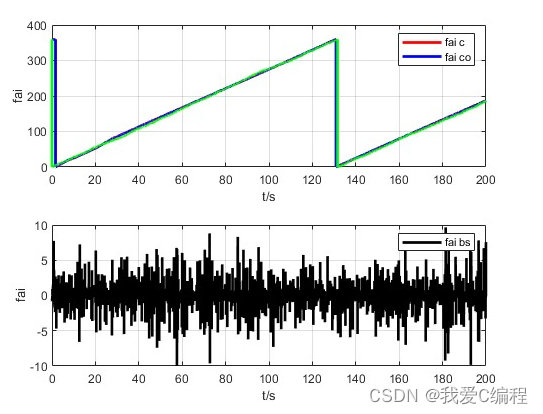
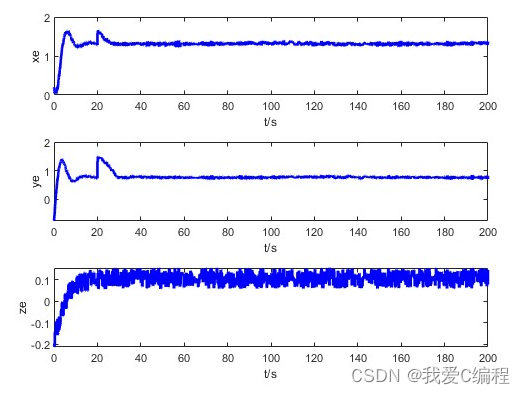
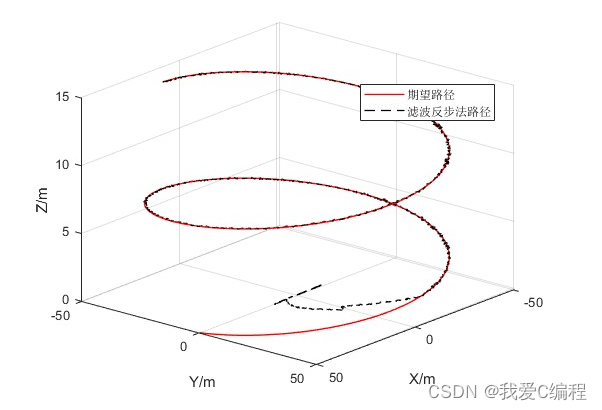
2.算法涉及理论知识概要

        自主水下航行器（Autonomous Underwater Vehicle，AUV）是一种具有自主性、灵活性、隐蔽性等优点的智能化设备，广泛应用于水下勘探、监测、搜救等任务。在AUV的运动控制中，需要考虑到水下环境的复杂性和不确定性，如水流、深度、海浪等因素都会对AUV的运动控制产生影响。因此，如何设计一种能够有效应对水下环境干扰的多自由度AUV运动控制算法是一个重要的问题。

      基于万能逼近原理自适应模糊控制算法的多自由度AUV运动控制抗干扰补偿算法采用了自适应模糊控制和抗干扰补偿技术，其主要思路如下：

  1. 建立多自由度AUV的数学模型，包括姿态、速度、加速度等状态变量，以及控制输入变量，如推力、转矩等。这是设计任何控制算法的第一步，在AUV的运动控制中，需要考虑到多自由度的运动状态变量，这包括位置、速度、角度、角速度和加速度等多个方面，同时需要考虑到控制输入变量，如推力、转矩等。

  2. 设计自适应模糊控制器，该控制器包括模糊推理机和自适应机制两部分。模糊推理机用于将输入的状态变量映射为控制输入，自适应机制用于不断更新模糊规则的参数，以适应不同的工作环境和干扰情况。模糊控制器是一种基于模糊推理的控制器，通过模糊推理机将输入的状态变量映射成为控制输入，以实现对多自由度AUV的控制。而自适应机制是指通过对模糊规则参数的不断调整来适应不同的环境和干扰情况，从而实现控制系统的自适应性和鲁棒性。具体地，自适应机制可以通过反馈控制来不断更新模糊规则中的参数，使其能够更加准确地描述AUV的运动状态和控制输入之间的关系。

  3. 设计抗干扰补偿器，该补偿器用于抵消水下环境的干扰，包括水流、深度、海浪等因素。水下环境的复杂性和不确定性，使得AUV的运动控制受到各种干扰，如水流、深度变化、海浪等因素都会影响AUV的运动轨迹和控制输入。因此，设计一种有效的抗干扰补偿器是非常重要的。抗干扰补偿器可以通过对水下环境的实时监测和分析，采用补偿控制策略对控制输入进行调整，以抵消水下环境干扰，保证AUV的运动控制精度和稳定性。

  4. 将自适应模糊控制器和抗干扰补偿器组合起来，形成多自由度AUV的运动控制系统。在控制过程中，自适应模糊控制器根据当前状态变量的值计算出控制输入，抗干扰补偿器则根据环境的干扰程度对控制输入进行补偿，从而实现多自由度AUV的精确控制。

三、算法特点

与传统的控制算法相比，基于万能逼近原理自适应模糊控制算法的多自由度AUV运动控制抗干扰补偿算法具有以下特点：

  1. 自适应性强：该算法采用自适应模糊控制和抗干扰补偿技术，能够根据环境干扰的程度自适应地调整控制输入，实现多自由度AUV的精确控制。相较于传统的固定控制器，自适应控制器能够更好地适应不同的工作环境和干扰情况，提高控制系统的稳定性和鲁棒性。

  2. 抗干扰性强：该算法通过抗干扰补偿器对水下环境的干扰进行补偿，能够有效地应对水流、深度、海浪等因素对多自由度AUV运动控制的影响，提高控制系统的鲁棒性。抗干扰补偿器能够实时监测和分析水下环境的变化，并根据干扰的程度对控制输入进行调整，以保证AUV的运动控制精度和稳定性。

  3. 精度高：该算法采用模糊控制器对状态变量进行映射，能够实现对多自由度AUV的精确控制，提高控制系统的控制精度。相较于传统的控制器，模糊控制器能够处理数据的模糊性和不确定性，更适合应对水下环境的复杂性和不确定性，提高了控制系统的稳定性和可靠性。

  4. 可扩展性强：该算法具有较强的可扩展性，能够根据不同的应用需求进行调整和扩展，适用于多种水下环境下的AUV运动控制应用。同时，该算法还可以应用于其他领域的自适应控制问题，如机器人控制、飞行器控制等，具有广泛的应用前景和研究价值。

3.MATLAB核心程序

 

.................................................................................figure;
subplot(211);
plot(t1,mod(fai_c,360),'r','linewidth',2);
hold on
plot(t2,mod(fai_co,360),'b','linewidth',2);
hold on
plot(t1(1:end),faiback(1:end),'g','linewidth',2);
grid on
legend('fai c','fai co');
xlabel('t/s');
ylabel('fai');load fai_bs.mat
t3=ans.Time;
fai_bs=ans.Data;
subplot(212);
plot(t3(50:end),fai_bs(50:end),'k','linewidth',2);
grid on
legend('fai bs');
xlabel('t/s');
ylabel('fai');load theta_c.mat
t1=ans.Time;
theta_c=ans.Data;load theta_co.mat
t2=ans.Time;
theta_co=ans.Data;figure;
subplot(211);
plot(t1,theta_c,'r','linewidth',2);
hold on
plot(t2,theta_co,'b','linewidth',2);
grid on
legend('theta c','theta co');
xlabel('t/s');
ylabel('theta');
load theta_bs.mat
t3=ans.Time;
theta_bs=ans.Data;
subplot(212);
plot(t3(50:end),theta_bs(50:end),'k','linewidth',2);
grid on
legend('theta bs');
xlabel('t/s');
ylabel('theta');
axis([0,200,-3,3]);load u_c.mat
t1=ans.Time;
u_c=ans.Data;load u_co.mat
t2=ans.Time;
u_co=ans.Data;figure;
subplot(211);
plot(t1,u_c,'r','linewidth',2);
hold on
plot(t2,u_co,'b','linewidth',2);
grid on
legend('u c','u co');
xlabel('t/s');
ylabel('u');load u_bs.mat
t3=ans.Time;
u_bs=ans.Data;
subplot(212);
plot(t3(50:end),u_bs(50:end),'k','linewidth',2);
grid on
legend('u bs');
xlabel('t/s');
ylabel('u');load rc.mat
t1=ans.Time;
rc=ans.Data(:);load rco.mat
t2=ans.Time;
rco=ans.Data(:);t3=ans.Time;
rback=ans.Data(:);figure;
subplot(211);
plot(t1(50:end),rc(50:end),'r','linewidth',2);
hold on
plot(t2(50:end),rco(50:end),'b','linewidth',2);
hold on
plot(t2(50:end),rback(50:end),'g','linewidth',2);
grid on
legend('r c','r co','r');
xlabel('t/s');
ylabel('r');load rbs.mat
t3=ans.Time;
rbs=ans.Data(:);
subplot(212);
plot(t3,rbs,'k','linewidth',2);
grid on
legend('r bs');
xlabel('t/s');
ylabel('r');load qc.mat
t1=ans.Time;
qc=ans.Data(:);load qco.mat
t2=ans.Time;
qco=ans.Data(:);load qback.mat
t3=ans.Time;
qback=ans.Data(:);figure;
subplot(211);
plot(t1(50:end),qc(50:end),'r','linewidth',2);
hold on
plot(t2(50:end),qco(50:end),'b','linewidth',2);
hold on
plot(t3(50:end),qback(50:end),'g','linewidth',2);
grid on
legend('q c','q co','q');
xlabel('t/s');
ylabel('q');
axis([0,200,-6,2]);
load qbs.mat
t3=ans.Time;
qbs=ans.Data(:);
subplot(212);
plot(t3,qbs,'k','linewidth',2);
grid on
legend('q bs');
xlabel('t/s');
ylabel('q');figure;load xe.mat
t1=ans.Time;
xe=ans.Data(:);
subplot(311);
plot(t1(50:end),xe(50:end),'b','linewidth',2);
xlabel('t/s');
ylabel('xe');
load ye.mat
t2=ans.Time;
ye=ans.Data(:);
subplot(312);
plot(t2(50:end),ye(50:end),'b','linewidth',2);
xlabel('t/s');
ylabel('ye');
load ze.mat
t3=ans.Time;
ze=ans.Data(:);
subplot(313);
plot(t3(50:end),ze(50:end),'b','linewidth',2);
xlabel('t/s');
ylabel('ze');Len=length(xe);
%标准路径
s = [14/Len:14/Len:14]';
load XYZ.mat load XX2.mat
x2= ans.Data(:);
load YY2.mat
y2= ans.Data(:);
load ZZ2.mat
z2= ans.Data(:);
figure;
plot3(x,y,z,'r','linewidth',1);
hold on
plot3(x2,y2,z2,'k--','linewidth',1);
hold on
legend('期望路径','滤波反步法路径');
xlabel('X/m');
ylabel('Y/m');
zlabel('Z/m');
grid on
view([130,26]);figure;
plot3(x,y,z,'r','linewidth',1);
hold on
plot3(x2,y2,z2,'k--','linewidth',1);
hold on
legend('期望路径','滤波反步法路径');
xlabel('X/m');
ylabel('Y/m');
zlabel('Z/m');
grid on
view([180,90]);figure;
plot3(x,y,z,'r','linewidth',1);
hold on
plot3(x2,y2,z2,'k--','linewidth',1);
hold on
legend('期望路径','滤波反步法路径');
xlabel('X/m');
ylabel('Y/m');
zlabel('Z/m');
grid on
view([180,0]);figure;load Fu.mat
t1=ans.Time;
Fu=ans.Data(:);
subplot(311);
plot(t1(50:end),Fu(50:end),'b','linewidth',2);grid on
xlabel('t/s');
ylabel('Fu');
load delta_s.mat
t2=ans.Time;
delta_s=ans.Data(:);
subplot(312);
plot(t2(50:end),delta_s(50:end),'b','linewidth',2);grid on
xlabel('t/s');
ylabel('delta_s');
load delta_r.mat
t3=ans.Time;
delta_r=ans.Data(:);
subplot(313);
plot(t3(50:end),delta_r(50:end),'b','linewidth',2);grid on
xlabel('t/s');
ylabel('delta_r');figure;load uback.mat
t1=ans.Time;
uback=ans.Data(:);
subplot(311);
plot(t1(50:end),uback(50:end),'b','linewidth',2);
xlabel('t/s');
ylabel('u');
grid on
load vback.mat
t2=ans.Time;
vback=ans.Data(:);
subplot(312);
plot(t2(50:end),vback(50:end),'b','linewidth',2);
xlabel('t/s');
ylabel('v');
grid on
load wback.mat
t3=ans.Time;
wback=ans.Data(:);
subplot(313);
plot(t3(50:end),wback(50:end),'b','linewidth',2);
xlabel('t/s');
ylabel('w');
grid onfigure;load faiback.mat
t1=ans.Time;
faiback=ans.Data(:);
subplot(211);
plot(t1(1:end),faiback(1:end),'b','linewidth',2);
xlabel('t/s');
ylabel('fai');
grid onload thetaback.mat
t2=ans.Time;
thetaback=ans.Data(:);
subplot(212);
plot(t2(1:end),thetaback(1:end),'b','linewidth',2);
xlabel('t/s');
ylabel('theta');
grid on
axis([0,200,0,360]);
08_076_m

4.完整算法代码文件

V

这篇关于m基于万能逼近原理自适应模糊控制算法的多自由度AUV运动控制抗干扰补偿simulink仿真的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/705335。

相关文章

Java中流式并行操作parallelStream的原理和使用方法

Java中流式并行操作parallelStream的原理和使用方法

《Java中流式并行操作parallelStream的原理和使用方法》本文详细介绍了Java中的并行流（parallelStream）的原理、正确使用方法以及在实际业务中的应用案例,并指出在使用并行流... 目录Java中流式并行操作parallelStream0. 问题的产生1. 什么是parallelS
阅读更多...
Java中Redisson 的原理深度解析

Java中Redisson 的原理深度解析

《Java中Redisson的原理深度解析》Redisson是一个高性能的Redis客户端,它通过将Redis数据结构映射为Java对象和分布式对象,实现了在Java应用中方便地使用Redis,本文... 目录前言一、核心设计理念二、核心架构与通信层1. 基于 Netty 的异步非阻塞通信2. 编解码器三、
阅读更多...
Java HashMap的底层实现原理深度解析

Java HashMap的底层实现原理深度解析

《JavaHashMap的底层实现原理深度解析》HashMap基于数组+链表+红黑树结构,通过哈希算法和扩容机制优化性能,负载因子与树化阈值平衡效率,是Java开发必备的高效数据结构,本文给大家介绍... 目录一、概述：HashMap的宏观结构二、核心数据结构解析1. 数组（桶数组）2. 链表节点（Node
阅读更多...
深入理解Mysql OnlineDDL的算法

深入理解Mysql OnlineDDL的算法

《深入理解MysqlOnlineDDL的算法》本文主要介绍了讲解MysqlOnlineDDL的算法,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小... 目录一、Online DDL 是什么？二、Online DDL 的三种主要算法2.1COPY（复制法）
阅读更多...
Redis中Hash从使用过程到原理说明

Redis中Hash从使用过程到原理说明

《Redis中Hash从使用过程到原理说明》RedisHash结构用于存储字段-值对,适合对象数据,支持HSET、HGET等命令,采用ziplist或hashtable编码,通过渐进式rehash优化... 目录一、开篇：Hash就像超市的货架二、Hash的基本使用1. 常用命令示例2. Java操作示例三
阅读更多...
Redis中Set结构使用过程与原理说明

Redis中Set结构使用过程与原理说明

《Redis中Set结构使用过程与原理说明》本文解析了RedisSet数据结构,涵盖其基本操作（如添加、查找）、集合运算（交并差）、底层实现（intset与hashtable自动切换机制）、典型应用场... 目录开篇：从购物车到Redis Set一、Redis Set的基本操作1.1 编程常用命令1.2 集
阅读更多...
Redis中的有序集合zset从使用到原理分析

Redis中的有序集合zset从使用到原理分析

《Redis中的有序集合zset从使用到原理分析》Redis有序集合(zset)是字符串与分值的有序映射,通过跳跃表和哈希表结合实现高效有序性管理,适用于排行榜、延迟队列等场景,其时间复杂度低,内存占... 目录开篇：排行榜背后的秘密一、zset的基本使用1.1 常用命令1.2 Java客户端示例二、zse
阅读更多...
基于Python开发Windows自动更新控制工具

基于Python开发Windows自动更新控制工具

《基于Python开发Windows自动更新控制工具》在当今数字化时代,操作系统更新已成为计算机维护的重要组成部分,本文介绍一款基于Python和PyQt5的Windows自动更新控制工具,有需要的可... 目录设计原理与技术实现系统架构概述数学建模工具界面完整代码实现技术深度分析多层级控制理论服务层控制注
阅读更多...
Redis中的AOF原理及分析

Redis中的AOF原理及分析

《Redis中的AOF原理及分析》Redis的AOF通过记录所有写操作命令实现持久化,支持always/everysec/no三种同步策略,重写机制优化文件体积,与RDB结合可平衡数据安全与恢复效率... 目录开篇：从日记本到AOF一、AOF的基本执行流程1. 命令执行与记录2. AOF重写机制二、AOF的
阅读更多...
java程序远程debug原理与配置全过程

java程序远程debug原理与配置全过程

《java程序远程debug原理与配置全过程》文章介绍了Java远程调试的JPDA体系,包含JVMTI监控JVM、JDWP传输调试命令、JDI提供调试接口,通过-Xdebug、-Xrunjdwp参数配... 目录背景组成模块间联系IBM对三个模块的详细介绍编程使用总结背景日常工作中，每个程序员都会遇到bu
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2