本文主要是介绍每天五分钟深度学习:如何理解梯度下降算法可以逼近全局最小值?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文重点
上节课程中,我们已经知道了逻辑回归的代价函数J。要想最小化代价函数,我们需要使用梯度下降算法。
梯度下降算法地直观理解:
为了可视化,我们假设w和b都是单一实数,实际上,w可以是更高地维度。
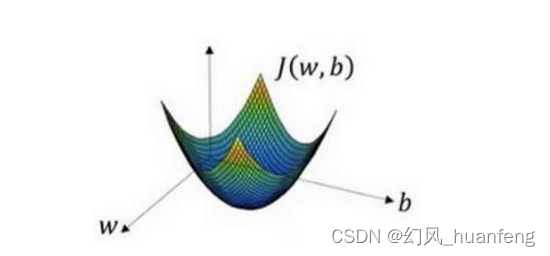
代价函数J是在水平轴w和b上的曲面,因此曲面的高度就是J(w,b)在某一点(w,b)的函数值。我们要做的就是找到使得代价函数J最小的值所对应地w和b。
从逻辑回归的损失函数来看梯度下降
因为我们定义的逻辑回归的是凸优化的问题,也就是说只有一个最优值,所以无论在哪里初始化,梯度下降都可以达到同一个局部最优点。梯度下降算法过程表示为:
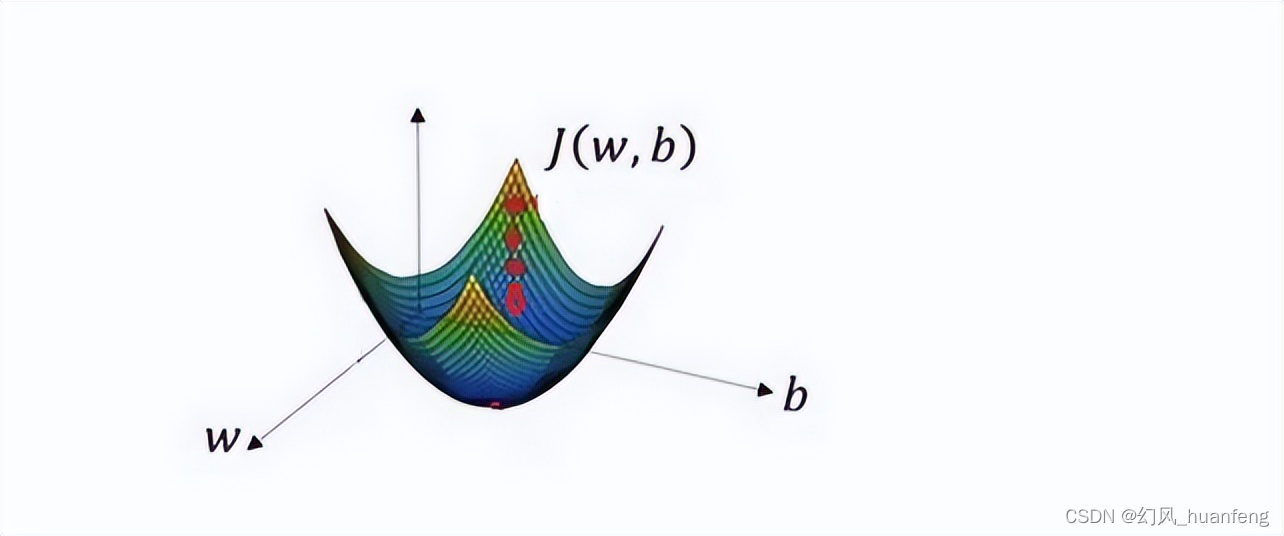
直到走到全局最优解或者接近全局最优解的地方,此时的w和b就是我们要找的w和b了,那么此时的损失函数最小,此时的目标函数最拟合数据。
梯度下降算法细节化说明:
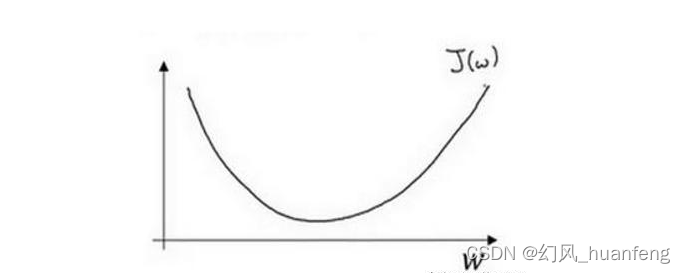
为了让大家对梯度下降算法能够有更加深刻的理解,上面我们有两个参数w和b,这里我们只是用一个参数w。
 </
</
这篇关于每天五分钟深度学习:如何理解梯度下降算法可以逼近全局最小值?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





