通滤波专题
运算放大器(运放)低通滤波反相放大器电路和积分器电路
低通滤波反相放大器电路 运放积分器电路请访问下行链接 运算放大器(运放)积分器电路 设计目标 输入ViMin输入ViMax输出VoMin输出VoMaxBW:fp电源Vee电源Vcc–0.1V0.1V–2V2V2kHz–2.5V2.5V 设计说明 这款可调式低通反相放大器电路可将信号电平放大 26dB 或 20V/V。R2 和 C1 可设置此电路的截止频率。此电路的频率响应与无源 RC 滤
ActiViz中的低通滤波
文章目录 一、低通滤波简介二、理想低通滤波器1、理想低通滤波器原理2、vtkImageIdealLowPass的常用函数3、vtkImageIdealLowPass的示例代码4、理想低通滤波器的注意事项 三、巴特沃斯低通滤波器1、巴特沃斯低通滤波器详细原理2、vtkImageButterworthLowPass的常用函数3、vtkImageButterworthLowPass的示例代码4、巴
高通滤波的第一个值特别大异常怎行消除
在使用高通滤波器处理信号时,遇到的第一个值特别大或出现异常的现象通常是由于滤波器的初始状态未设置导致的。这是滤波器初始条件未适应到数据特性所致,尤其是在滤波器的状态变量在开始时未正确初始化。解决这个问题的一种方法是在处理数据之前预先设置滤波器的状态,或者简单地丢弃开始几个可能受初始状态影响的数据点。下面是一些处理这种情况的建议: 方法1: 使用 lfilter_zi 设置初始状态 scipy.
(2024,超分辨率,膨胀卷积和低通滤波,SD)FouriScale:免训练高分辨率图像合成的频率视角
FouriScale: A Frequency Perspective on Training-Free High-Resolution Image Synthesis 公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群) 目录 0. 摘要 2. 相关工作 2.2 通过扩散模型进行高分辨率合成 3. 方法 3.1 符号表示 3.
图像的频域滤波-高通滤波
图像的频域滤波-高通滤波 介绍 这里的高通滤波主要是巴特沃兹高通和理想高通,其频率特性正好和对应的低通相反,这里就不再赘述。 效果图 可见,理想高通仍有振铃效应的产生,而巴特沃兹就好很多。加强滤波是为了弥补一下低频信息,让图像看上去更有意思一点哈。 示例代码 clc;clear all;close all;J=imread('lena.jpg');if size(J,
图像的频域滤波-低通滤波
图像的频域滤波-低通滤波 1.理想低通滤波 介绍 如图,通带内留下,阻带内直接干掉。 效果 理想低通最大的缺点就是会产生振铃效应,从滤波后结果的图片就可以发现(有一圈圈波纹的感觉)。 实例代码 clc;clear all;close all;%理想低通滤波器所产生的模糊和振铃现象 I=imread('lena.jpg');if size(I, 3)=
嵌入式C语言使用低通滤波、高通滤波、互补滤波算法
文章目录 一、一阶低通滤波算法1.1 公式1.2 C代码 二、一阶高通滤波算法2.1 公式2.2 C代码三、互补滤波算法3.1 前言3.2 公式3.2 C代码 一、一阶低通滤波算法 低通滤波(Low Pass Filter)用于从一个信号中去除高于某个频率的成分。它的基本原理是,信号中高于某个频率的成分在信号传输或接收过程中会发生衰减,而低于该频率的成分则不受影响。因此,通
一阶RC低通滤波电路推演与仿真
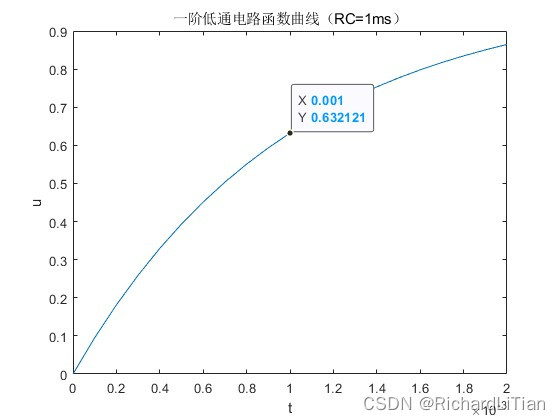
一阶RC低通滤波电路微分方程式推导 RC一阶低通滤波电路图如下图所示, 根据基尔霍夫电流定理,由图可知, i = C d u 0 d t \begin{aligned} i=C\frac{du_0}{dt} \end{aligned} i=Cdtdu0 根据基尔霍夫电压定理,由图可知, R C d u 0 d t + u 0 = u i \begin{aligned} \\RC\fr
低通滤波opencv
理论基础知识,高通部分已经讲过,这里不重复了。本部分做低通滤波,保留细节。即频谱中间部分保留,与高通相反。 import cv2import numpy as npimport matplotlib.pyplot as plto=cv2.imread('image\\lena256.bmp',0) #读入图片dft=cv2.dft(np.float32(o),flags=cv2.D
MATLAB实现高通滤波(附完整代码)
1.MATLAB实现高通滤波器 以下是一个使用MATLAB实现高通滤波器的例子。在这个例子中,我们将设计一个简单的数字高通滤波器,然后将其应用到一个包含低频和高频成分的信号上。 clc;close all;clear all;warning off;%清除变量 rand('seed', 500); randn('seed', 300); format long g; % 创建时间向
matlab理想带通滤波
理想带通使用如下函数,dim是维度,如果input是一维,则dim=1 % FILTERED = ideal_bandpassing(INPUT,DIM,WL,WH,SAMPLINGRATE)% % Apply ideal band pass filter on INPUT along dimension DIM.% % WL: lower cutoff frequency o
传感数据分析——高通滤波与低通滤波
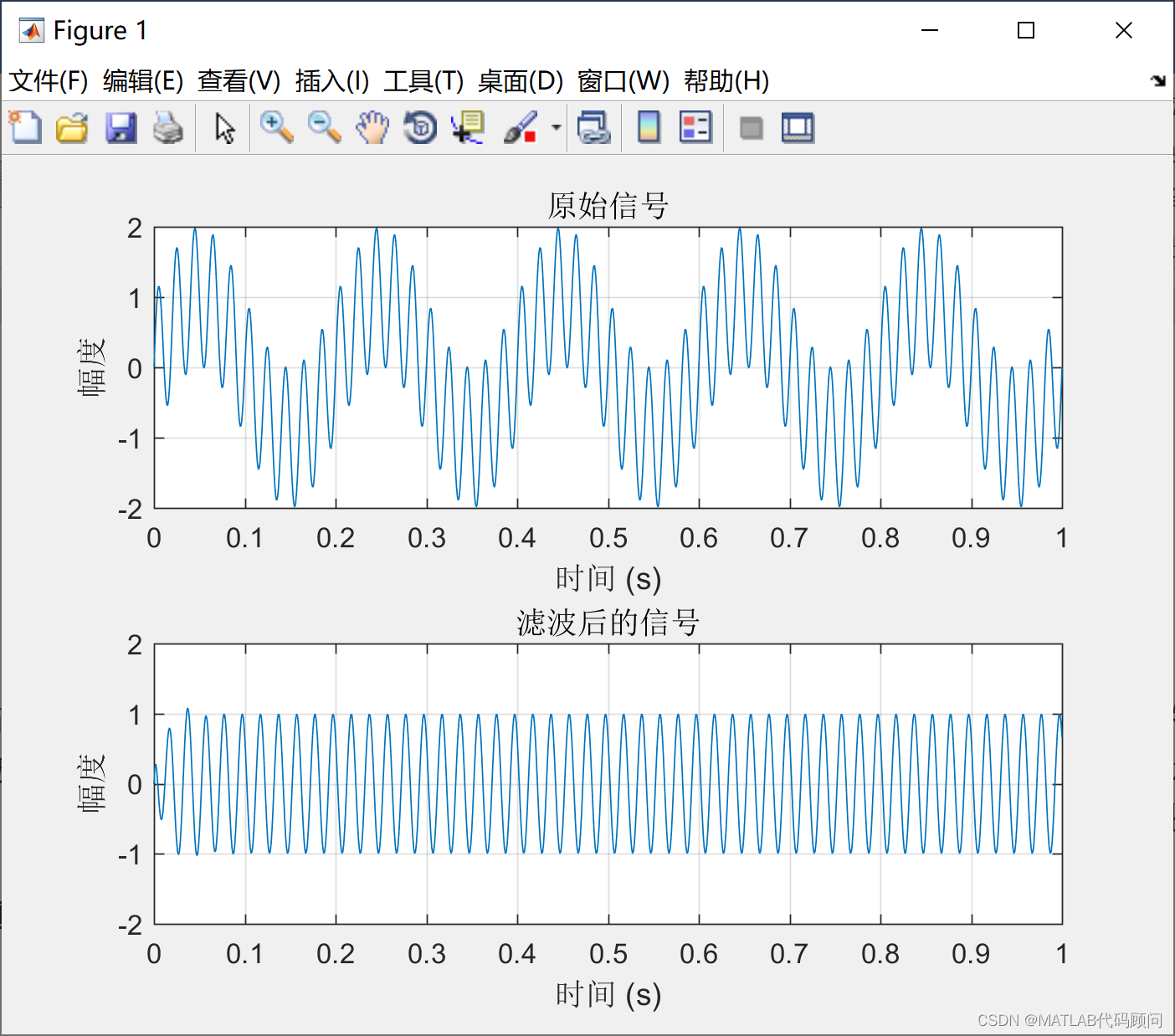
传感数据分析——高通滤波与低通滤波 文章目录 传感数据分析——高通滤波与低通滤波前言一、运行环境二、Python实现总结 前言 对于传感信号而言,我们可以提取其中的高频信息和低频信息,低频信息往往是信号的趋势,高频信息往往是一些突变或异常的信号,根据实际需求分离信号中的高低频特征具有实际意义。本文将使用scipy库中的signal模块实现高低通滤波器的设计,并采用计算周期特
RC低通滤波电路直接带载后会发生什么?
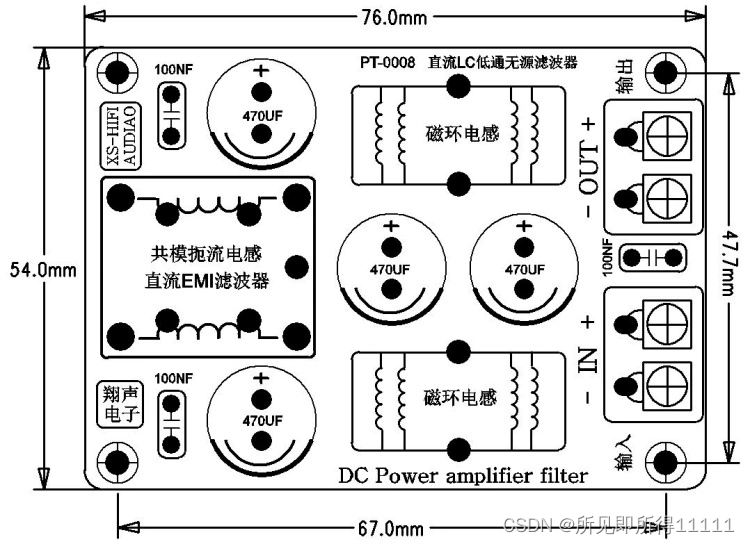
1、滤波的含义 滤波是频域范畴,它说的是不同频率的信号经过一个电路处理后,信号发生变化的问题,变化包含了原始信号幅值和相位的变化,滤波电路对信号的幅值做出的响应称为幅频响应,对信号相位做出的反应称为相频响应。每一个频率的信号对应在时域就是信号的充放电特性。 滤波通常借助动态器件如电感和电容,利用它们在不同频率下阻抗变化,从而在其上面产生压降,对我们需要去除的信号进行衰减,从而达到滤波的效果。
VTK修炼之道42:频域处理_高通滤波(理想+巴特沃兹)
1.理想高通滤波器 高通滤波与低通滤波正好相反,是频域图像的高频部分通过而抑制低频部分。在图像中图像的边缘对应高频分量,因此高通滤波的效果是图像锐化。同样最简单的高通滤波器是理想高通滤波器。通过设置一个频率阈值,将高于该阈值的频率部分通过,而低于阈值的低频部分设置为0。 VTK中理想高通滤波的实例如下: #include <vtkAutoInit.h>VTK_MODULE_INIT(v
VTK修炼之道41:频域处理_低通滤波(理想+巴特沃兹)
1.低通滤波器 低通滤波是将频域图像中的高频部分滤除而通过低频部分。图像的边缘和噪声对应于频域图像中的高频部分,而低通滤波的作用即是减弱这部分的能量,从而达到图像平滑去噪的目的。 2.理想低通滤波器 最简单的低通滤波器是理想低通滤波器,基本思想是给定一个频率阈值,将高于该阈值的所有部分设置为0,而低于该频率的部分保持不变。 理想是指该滤波器不能用电子元器件来实现,但是可以
VTK_Learning_频域处理_低通滤波(理想+巴特沃兹)
1.低通滤波器 低通滤波是将频域图像中的高频部分滤除而通过低频部分。图像的边缘和噪声对应于频域图像中的高频部分,而低通滤波的作用即是减弱这部分的能量,从而达到图像平滑去噪的目的。 2.理想低通滤波器 最简单的低通滤波器是理想低通滤波器,基本思想是给定一个频率阈值,将高于该阈值的所有部分设置为0,而低于该频率的部分保持不变。 理想是指该滤波器不能用电子元器件来实现,但是可以通过计算机
全通滤波的级联实现EQ filter(一)
上一篇文章引入了dynamic EQ这个概念,就是动态EQ的意思,就是EQfilter的系数是按照sample点实时更新的。目前EQ filter都是使用biquard,filter type包括lowpass/highpass/bandpass/lowshelf/highshelf/peaking filter,每种滤波器有cutofffrequency/Q/gain这三个参数可
11. 对一幅灰度图像增加高频噪声,再对其进行频域低通滤波。
#include <cv.h>#include <highgui.h> //图像视频输出/输入头文件using namespace std;IplImage* AddGuassianNoise(IplImage* src) //添加高斯噪声{IplImage* dst = cvCreateImage(cvGetSize(src), src->depth, src->nChannel
对传感器采样数据的低通滤波
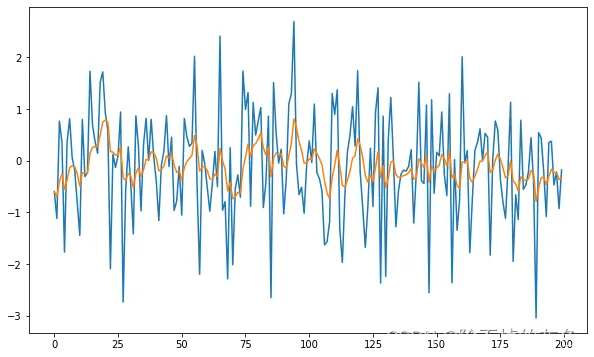
低通滤波(Low-pass filter) 是一种过滤方式,规则为低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱。 一阶低通数字滤波器 滤波系数a越小,滤波结果越平稳,但是灵敏度低;滤波系数a越大,滤波结果越不稳定,但是灵敏度高; filterDesigner 或者 fdatool fdatool——Filter Designer App
Matlab 一阶低通滤波/一阶IIR
LPF 一阶低通滤波 同样拿那个炸机气压计日志分析,可以更好对比 新建变量,把高度存进去BaroAlt.mat写获取高度值函数写LPF函数 function output = LPF(x)persistent lastx Initif isempty(Init)lastx = x;Init = 1;endalpha = 0.9;output = alpha*lastx + (1 - al