本文主要是介绍(2024,超分辨率,膨胀卷积和低通滤波,SD)FouriScale:免训练高分辨率图像合成的频率视角,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
FouriScale: A Frequency Perspective on Training-Free High-Resolution Image Synthesis
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)

目录
0. 摘要
2. 相关工作
2.2 通过扩散模型进行高分辨率合成
3. 方法
3.1 符号表示
3.2 通过膨胀卷积实现结构一致性
3.3 通过低通滤波实现尺度一致性
3.4 适应任意尺寸的生成
3.5 FouriScale 指导
3.6 详细设计
4. 实验
5. 结论和限制
0. 摘要
在这项研究中,我们深入探讨了从预训练的扩散模型生成高分辨率图像的过程,解决了模型应用于超出其训练分辨率时出现的重复图样(pattern)和结构失真等长久挑战。为了解决这个问题,我们从频域分析的角度引入了一种创新的、无需训练的方法 FouriScale。我们通过结合膨胀和低通滤波来替换预训练扩散模型中原始的卷积层,旨在分别实现跨分辨率的结构一致性和尺度一致性。通过进一步采用填充后裁剪(padding-then-crop)的策略进行增强,我们的方法能够灵活处理各种长宽比的文本到图像的生成。通过使用 FouriScale 作为指导,我们的方法成功平衡了生成图像的结构完整性和保真度,实现了任意尺寸、高分辨率和高质量生成的惊人能力。由于其简单性和兼容性,我们的方法可以为未来超高分辨率图像合成的探索提供宝贵的见解。
项目页面:https://github.com/LeonHLJ/FouriScale

2. 相关工作
2.2 通过扩散模型进行高分辨率合成
高分辨率合成一直受到广泛关注。先前的工作主要集中在优化噪声计划 [7, 22],开发级联架构 [20, 37, 42] 或去噪专家混合 [2] 来生成高分辨率图像。尽管它们具有令人印象深刻的能力,但扩散模型通常受到特定分辨率约束的限制,并且在不同长宽比和分辨率之间不能很好地泛化。
一些方法已尝试通过适应更广泛的分辨率范围来解决这些问题。例如,
- Any-size Diffusion [50] 对一组具有固定长宽比范围的图像进行了预训练 SD 的微调,类似于 SDXL [32]。
- FiT [28] 将图像视为 token 序列,并自适应地填充图像 token 以达到预定义的最大 token 限制,确保硬件友好的训练和灵活的分辨率处理。
然而,这些模型需要模型训练,忽视了预训练模型处理具有不同分辨率的图像生成的固有能力。
- 最近一些方法 [3,24,26] 尝试通过利用预训练的扩散模型拼接重叠补丁来生成全景图像。
- 最近的工作 [25] 探索了通过检查注意力熵来调整预训练的扩散模型以生成各种大小的图像。
- ElasticDiff [14] 使用默认分辨率的估计来指导任意尺寸图像的生成。
- 然而,ScaleCrafter [15] 发现通过预训练的扩散模型生成高分辨率图像的关键在于卷积层。他们提出了一种重新膨胀(re-dilation)和卷积分散操作(convolution disperse)来扩展卷积核大小,这需要对原始卷积核到扩展卷积核的线性转换进行离线计算。
- 相反,我们通过频域分析深入研究了重复模式的问题,并通过这一视角来处理它。我们方法的简单性消除了任何离线预计算的需要,有利于其兼容性和可扩展性。
3. 方法
3.1 符号表示
二维离散傅里叶变换(2D DFT)。给定一个二维离散信号 F(m, n),尺寸为 M × N,二维离散傅里叶变换(2D DFT)定义如下:
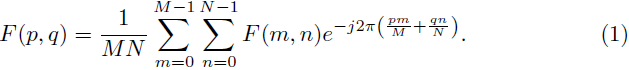
二维膨胀卷积(2D Dilated Convolution)。具有卷积核 k(m, n) 的膨胀卷积核,记为
![]()
过在原始卷积核的元素之间引入零来形成,如下所示:

其中 dh, dw 是高度和宽度上的膨胀因子,m 和 n 是膨胀空间中的索引。% 表示取模运算。
3.2 通过膨胀卷积实现结构一致性
扩散模型的去噪网络,记为 ϵθ,通常在特定分辨率 h × w 的图像或潜空间上进行训练。这个网络通常采用 U-Net 架构构建。我们的目标是在推断阶段使用去噪网络 ϵθ 的参数生成一个分辨率更高的 H × W 图像,而无需重新训练。

如前所述,当推断分辨率变大时,U-Net 中的卷积层往往会导致模式重复出现。为了防止推断分辨率时的结构失真,我们采用在默认分辨率和高分辨率之间建立结构一致性的方法,如图 2 所示。特别是,对于 U-Net 中的卷积层 Conv_k 及其卷积核 k,以及高分辨率输入特征图 F,结构一致性可以如下表示:
![]()
其中,Down_s 表示缩小采样操作,缩放因子为 s,⊛ 表示卷积操作。(为了简化起见,我们假设高度和宽度的缩小采样比例相等。在这种情况下,我们的方法也可以通过我们的填充-裁剪策略(第 3.4 节)来适应不同的缩小采样比例。)这个方程暗示着需要为更大的分辨率定制一个新的卷积核 k′。然而,由于特征图 F 的多样性,找到一个合适的 k′ 可能具有挑战性。最近的 ScaleCrafter [15] 方法使用结构级和像素级校准来学习卷积核 k 和 k′ 之间的线性转换,但是为每个新的卷积核大小和新的目标分辨率学习一个新的转换可能会很繁琐。
在这项工作中,我们提出从频率的角度处理结构一致性。假设输入 F(x, y) ∈ R^(H_f × W_f × C),它是一个二维离散空间信号。沿着 x 和 y 轴的采样率分别由 Ωx 和 Ωy 给出。F(x, y) 的傅里叶变换表示为 F(u, v) ∈ R_(H_f × W_f × C)。在这种情况下,沿着 u 和 v 轴的最高频率分别表示为 umax 和 vmax。此外,降采样特征图 Down_s(F(x, y)) 的傅里叶变换,其尺寸缩减为 R^(Hf / s × Wf / s × C),表示为 F′(u, v)。
定理 1。空间降采样导致信号可以容纳的频率范围减小,特别是在频谱的高端。这个过程会导致高频率被折叠到低频率上,并叠加到原始低频率上。对于一维信号,在 s 步长的条件下,由于降采样导致的高低频率叠加可以数学上表示为
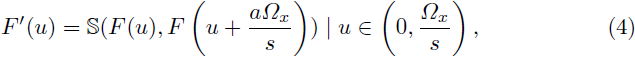
其中 S 表示叠加操作符,Ωx 是 x 轴上的采样率,a = 1, . . . , s − 1。
引理 1。对于一幅图像,使用步长 s 进行空间降采样的操作可以被视为将傅里叶谱分成 s × s 个相等的块,然后以平均缩放比例 1 / s^2 均匀地叠加这些块。

其中 F_(i,j) (u, v) 是由将 F(u, v) 均匀分成 s×s 个不重叠的块得到的 F(u, v) 的子矩阵,i, j ∈ {0, 1, . . . , s − 1}。 定理 1 和引理 1 的证明见附录(第 A.1 节和第 A.2 节)。它们描述了空间降采样所施加的在频域中的洗牌和叠加 [34, 47, 51]。如果我们将方程(3)转换到频域,并根据引理 1 的结论,我们可以得到:

其中,k(u, v)、k′(u, v) 分别表示卷积核 k 和 k′ 的傅里叶变换,⊙ 表示逐元素乘法。方程(6)表明,理想卷积核 k′ 的傅里叶谱应该由 s×s 卷积核 k 的傅里叶谱拼接而成。换句话说,k′ 的傅里叶谱中应该存在周期性重复,而这种重复的图样就是 k 的傅里叶谱。
幸运的是,广泛使用的膨胀卷积完全符合这一要求。假设具有尺寸 M × N 的卷积核 k(m, n),其膨胀版本是 k_(d_h,d_w) (m, n),膨胀因子为 (d_h, d_w)。对于 dh 的整数倍,即 p' = pd_h,以及 dw 的整数倍,即 q' = qd_w,膨胀卷积核在二维离散傅里叶变换(方程(1))中的指数项变为:
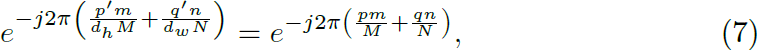
在 m 维度上具有 M 的周期,n 维度上具有 N 的周期。这表明,由原始卷积核 k 参数化的膨胀卷积核,膨胀因子为 (H/h,W/w),是理想的卷积核 k′。在图 3 中,我们直观地展示了膨胀卷积的周期重复性。我们注意到 [15] 也使用了膨胀操作。与 [15] 不同的是,我们的工作从频率分析的角度开始,并为其有效性提供了理论上的解释。

3.3 通过低通滤波实现尺度一致性
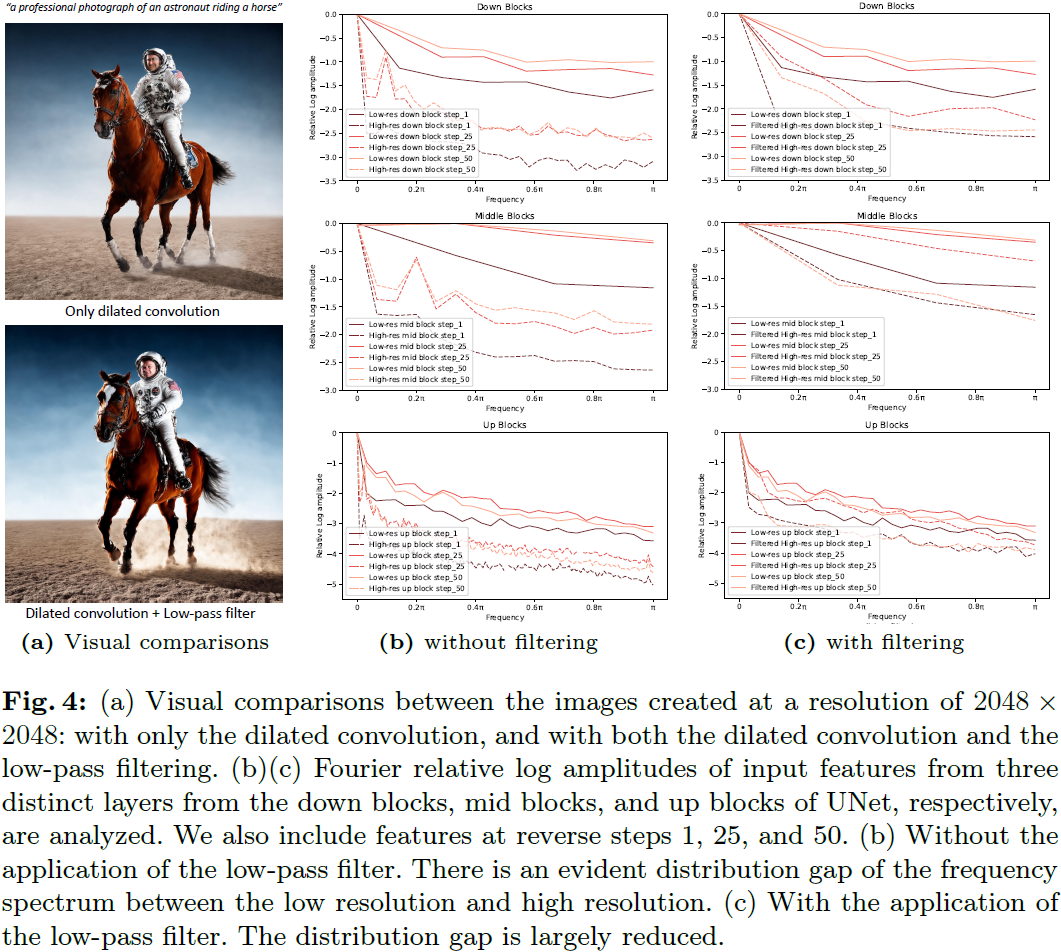
然而,在实践中,仅仅使用膨胀卷积不能很好地缓解图样重复的问题。如图 4a(左上角)所示,图样重复问题得到了显著减轻,但是某些细节,比如马的腿,仍然存在问题。这种现象是由于空间降采样后的混叠效应(aliasing effect)导致的,它提高了低分辨率特征和高分辨率下采样特征之间的分布差异,如图 4b 所示(图中实线和虚线之间的 gap)。混叠改变了原始信号的基本频率分量,破坏了其在不同尺度上的一致性。
(注:在 StyleGAN3 中也有解决伪影和混叠的措施)
(2021,StyleGAN3)无失真(Alias-Free)生成对抗网络_stylegan3
在本文中,我们引入了低通滤波操作,或称为频谱池化,以消除可能导致混叠(aliasing)的高频成分,旨在构建不同分辨率之间的尺度一致性。假设 F(m, n) 是一个具有分辨率 M × N 的二维离散信号。沿着高度和宽度分别按 sh 和 sw 缩小采样,将在频域中将奈奎斯特限制改为 M/(2sh) 和 N/(2sw),分别对应于每个维度上一半的新采样率。预期的低通滤波器应该移除这些新的奈奎斯特限制以上的频率,以防止混叠。因此,在低通滤波器中用于通过低频的最佳掩模尺寸(假设频谱是集中的)为 M/sh × N/sw。该滤波器设计确保在降分辨率时保留所有有价值的频率,同时通过过滤掉更高的频率来防止混叠。
如图 4c 所示,低通滤波器的应用导致高分辨率和低分辨率之间的频率分布更加接近。这确保了方程(3)的左侧产生一个合理的图像结构。另外,由于我们的目标是矫正图像结构,低通滤波不会有害,因为它通常保留信号的结构信息,主要存在于较低的频率分量中 [30,48]。
随后,最终的卷积核 k* 是通过对膨胀卷积核应用低通滤波来获得的。考虑到与膨胀卷积核相关的傅里叶谱的周期性特性,新卷积核 k* 的傅里叶谱涉及通过插入零频率来扩展原始卷积核 k 的谱。因此,这种扩展避免了将新的频率分量引入到新的卷积核 k* 中。在实践中,我们不直接计算卷积核 k∗,而是用以下等效操作替换原始的卷积层 Conv_k,以确保计算效率:
![]()
其中 H 表示低通滤波器。图 4a(左下角)说明了膨胀卷积和低通滤波的组合解决了模式重复的问题。

3.4 适应任意尺寸的生成
得出的结论仅适用于训练中使用的高分辨率图像和低分辨率图像的长宽比相同的情况。从方程(5)和方程(6)可以看出,当长宽比变化时,即沿着高度和宽度的膨胀率不同的情况下,低分辨率图像中构建良好的结构将会被扭曲和压缩,如图 5(a)所示。然而,在实际应用中,理想情况是预训练的扩散模型具有生成任意尺寸图像的能力。
我们引入了一种简单而有效的方法,称为填充-裁剪,来解决这个问题。图 5(b)展示了其有效性。实质上,当一个层接收到标准分辨率为 hf×wf 的输入特征,并且这个输入特征在推断期间增加到大小为 Hf×Wf 时,我们的第一步是将输入特征用零填充到大小为 r·hf × r·wf。这里,r 被定义为ceil(Hf / hf) 和 Ceil(Wf / wf) 的最大值,其中 Ceil 表示向上取整操作。填充操作假设我们的目标是生成大小为 rh×rw 的图像,其中某些区域填充了零。随后,我们应用方程(8)来矫正更高分辨率输出中重复模式的问题。最终,获得的特征被裁剪以恢复其预期的空间大小。这一步骤不仅是为了抵消零填充的影响,还是为了在分辨率增加时控制计算需求,特别是来自 UNet 架构中的自注意力层。考虑到计算效率,我们的等效解决方案如算法 1 所述。

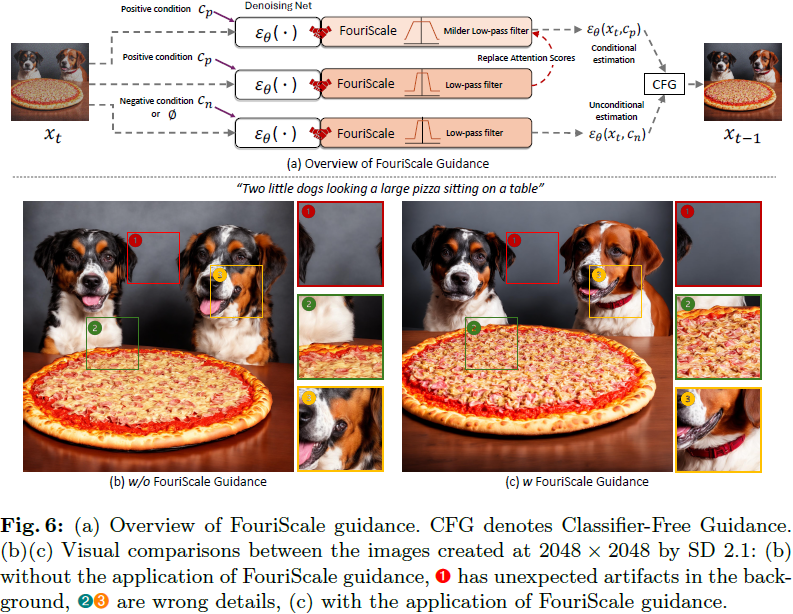
3.5 FouriScale 指导
在生成高分辨率图像时,FouriScale 有效地缓解了结构失真。然而,它会在背景中引入一定的伪影和意想不到的模式,如图 6(b)所示。根据我们的经验发现,我们确定主要问题源于在使用无分类器指导 [21] 生成条件估计(conditional estimation)时应用的低通滤波。这个过程通常会导致回响效应(ringing effect)和细节丢失。
为了提高图像质量并减少伪影,如图 6(a)所示,我们开发了 Fouriscale 的指导版本作为参考,旨在将富含细节的输出与其对齐。具体而言,除了通过 Fouriscale 修改的 UNet 导出的无条件和有条件估计之外,我们还生成了一个额外的有条件估计。这个估计受到相同的膨胀卷积的影响,但使用了更温和的低通滤波器来容纳更多的频率。我们用通过 Fouriscale 处理的有条件估计的注意力图替换它的注意力层的注意力图,这与图像编辑的精神类似。鉴于 UNet 的注意力图包含丰富的位置和结构信息,这种策略允许将由 Fouriscale 导出的正确结构信息纳入到生成中,同时减轻由低通滤波通常引起的图像质量下降和细节丢失。最终的噪声估计是根据无条件估计和新的有条件估计按照无分类器指导来确定的。正如我们在图 6(c)中所看到的,前述问题大部分得到了缓解。
3.6 详细设计
退火膨胀和滤波。由于图像结构主要在早期的反向步骤中勾勒出来,随后的步骤侧重于增强细节,我们为膨胀卷积和低通滤波都实现了一种退火方法。最初的 S_init 步骤,我们采用理想的膨胀卷积和低通滤波。在从 S_init 到 S_stop 的过程中,我们逐渐减小膨胀因子和 r(如算法 1 中详细说明),直至降到 1。在 S_stop 步之后,使用原始的 UNet 进一步细化图像细节。
SDXL 的设置。SDXL 通常在分辨率接近 1024×1024 像素的图像上进行训练,同时适应各种长宽比。我们的观察结果表明,使用理想的低通滤波器会导致 SDXL 的结果不佳。相反,一个更温和的低通滤波器,使用一个系数 σ∈[0,1](在我们的方法中设定为 0.6)来调节而不是完全消除高频元素,提供了更优越的视觉质量。这种现象可以归因于 SDXL 有效地处理尺度变化的能力,消除了维持尺度一致性需要理想低通滤波器的需求,从而证实了纳入低通滤波来解决尺度变异性的合理性。此外,对于SDXL,我们通过确定训练分辨率与目标分辨率的长宽比最接近的分辨率来计算比例因子 r(参考算法 1)。
4. 实验
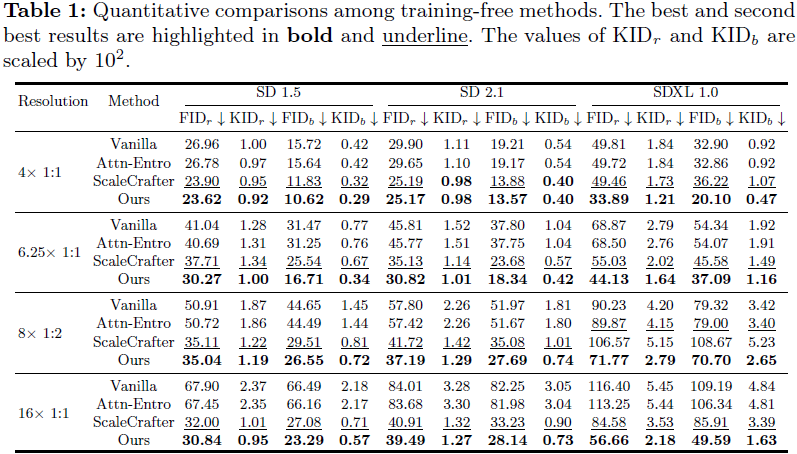
实验设置。我们遵循 [15] 在三个文本到图像模型上报告结果,包括 SD 1.5 [12]、SD 2.1 [10] 和SDXL 1.0 [32],生成四种更高分辨率的图像。测试的分辨率分别是其各自训练分辨率的 4×、6.25×、8× 和 16× 像素数。对于 SD 1.5 和 SD 2.1 模型,原始的训练分辨率设置为 512×512 像素,而推断分辨率分别为 1024×1024、1280×1280、2048×1024 和 2048×2048。在 SDXL 模型的情况下,它是在接近 1024×1024 像素的分辨率上进行训练的,而更高的推断分辨率为2048×2048、2560×2560、4096×2048 和 4096×4096。我们默认在所有实验设置中使用 FreeU [39]。
测试数据集和评估指标。根据 [15],我们使用 Laion-5B 数据集 [38] 进行性能评估,该数据集包含 50 亿对图像和相应的标题。对于在 1024×1024 推断分辨率上进行的测试,我们选择了 30,000 张图像的子集,每个图像与数据集中随机选择的文本提示配对。考虑到大量的计算需求,对于推断分辨率超过 1024×1024 的测试,我们将样本大小减少到 10,000 张图像。我们通过测量生成图像与真实图像之间的 Frechet Inception Distance(FID)[18] 和 Kernel Inception Distance(KID)[4] 来评估生成图像的质量和多样性,分别表示为 FIDr 和 KIDr。为了展示方法在新分辨率下保持预训练模型的原始能力,我们还遵循 [15] 来评估在基本训练分辨率和推断分辨率下生成图像之间的指标,分别表示为 FIDb 和 KIDb。

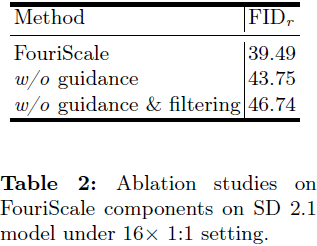

5. 结论和限制
我们提出了 FouriScale,一种新颖的方法,可以增强从预训练扩散模型生成高分辨率图像的能力。通过解决重复模式和结构失真等关键挑战,FouriScale 引入了一种基于频域分析的无训练方法,通过膨胀操作和低通滤波操作提高了不同分辨率下的结构和比例一致性。填充-裁剪策略的结合以及 FouriScale 指导的应用增强了文本到图像生成的灵活性和质量,适应了不同的长宽比,同时保持了结构完整性。FouriScale 的简单性和适应性,避免了任何广泛的预计算,为该领域树立了新的基准。
FouriScale 仍然面临着生成超高分辨率样本(例如 4096×4096 像素)的挑战,这些样本通常会出现意外的伪影。此外,它专注于卷积内的操作,限制了其适用范围,仅限于纯 transformer 型扩散模型。
这篇关于(2024,超分辨率,膨胀卷积和低通滤波,SD)FouriScale:免训练高分辨率图像合成的频率视角的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









