本文主要是介绍一阶RC低通滤波电路推演与仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一阶RC低通滤波电路微分方程式推导
RC一阶低通滤波电路图如下图所示,
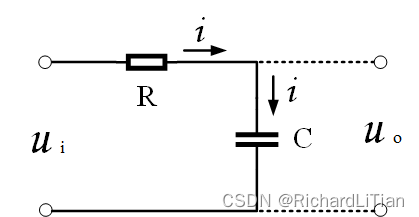
根据基尔霍夫电流定理,由图可知,
i = C d u 0 d t \begin{aligned} i=C\frac{du_0}{dt} \end{aligned} i=Cdtdu0
根据基尔霍夫电压定理,由图可知,
R C d u 0 d t + u 0 = u i \begin{aligned} \\RC\frac{du_0}{dt}+u_0&=u_i \end{aligned} RCdtdu0+u0=ui
将式子化为一阶线性微分方程,可得
d u 0 d t + 1 R C u 0 = u i R C \begin{aligned} \\\frac{du_0}{dt}+\frac{1}{RC}u_0&=\frac{u_i}{RC} \end{aligned} dtdu0+RC1u0=RCui
一阶线性方程微分的推导
接下来我们复习一下一阶线性微分方程通解的推导。
形如
d y d x + P ( x ) y = Q ( x ) \begin{aligned} \frac{dy}{dx}+P(x)y&=Q(x) \end{aligned} dxdy+P(x)y=Q(x)
的方程,称为一阶线性微分方程。
其中, P ( x ) P(x) P(x)、 Q ( x ) Q(x) Q(x)均为 x x x的已知函数, Q ( x ) Q(x) Q(x)称为已知项。
① 当 Q ( x ) = 0 Q(x)=0 Q(x)=0时,方程 y ′ + P ( x ) y = 0 y{'}+P(x)y=0 y′+P(x)y=0,此时方程为一阶齐次线性微分方程,那么
d y d x + P ( x ) y = 0 d y y = − P ( x ) d x \begin{aligned} \frac{dy}{dx}+P(x)y&=0 \\\frac{dy}{y}&=-P(x)dx \end{aligned} dxdy+P(x)yydy=0=−P(x)dx
两边积分,可得
l n y = − ∫ P ( x ) d x + l n C 1 \begin{aligned} lny&=-\int_{}^{}{P(x)dx}+lnC_1 \end{aligned} lny=−∫P(x)dx+lnC1
求得通解为
y = C 1 e − ∫ P ( x ) d x \begin{aligned} y&=C_1e^{-\int_{}^{}{P(x)dx}} \end{aligned} y=C1e−∫P(x)dx
② 当 Q ( x ) ≠ 0 Q(x)≠0 Q(x)=0 时,方程 y ′ + P ( x ) y = Q ( x ) y{'}+P(x)y=Q(x) y′+P(x)y=Q(x),此时方程为一阶非齐次线性微分方程,那么
d y d x + P ( x ) y = Q ( x ) d y y = [ − P ( x ) + Q ( x ) y ] d x \begin{aligned} \frac{dy}{dx}+P(x)y&=Q(x) \\\frac{dy}{y}&=[-P(x)+\frac{Q(x)}{y}]dx \end{aligned} dxdy+P(x)yydy=Q(x)=[−P(x)+yQ(x)]dx
两边积分,可得
l n y = − ∫ P ( x ) d x + ∫ Q ( x ) y d x + l n C 2 \begin{aligned} lny&=-\int_{}^{}{P(x)dx}+\int_{}^{}{\frac{Q(x)}{y}dx}+lnC_2 \end{aligned} lny=−∫P(x)dx+∫yQ(x)dx+lnC2
求得通解为
y = C 2 e ∫ Q ( x ) y d x ∙ e ∫ − P ( x ) d x \begin{aligned} y&=C_2e^{\int_{}^{}{\frac{Q(x)}{y}dx}} \bullet e^{\int_{}^{}{-P(x)dx}} \end{aligned} y=C2e∫yQ(x)dx∙e∫−P(x)dx
设 C 2 e ∫ Q ( x ) y d x = C ( x ) C_2e^{\int_{}^{}{\frac{Q(x)}{y}dx}}=C(x) C2e∫yQ(x)dx=C(x)
则有
y = C ( x ) e ∫ − P ( x ) d x y ′ = C ′ ( x ) e ∫ − P ( x ) d x − C ( x ) P ( x ) e ∫ − P ( x ) d x \begin{aligned} y&=C(x)e^{\int_{}^{}{-P(x)dx}} \\y{'}&=C{'}(x)e^{\int_{}^{}{-P(x)dx}}-C(x)P(x)e^{\int_{}^{}{-P(x)dx}} \end{aligned} yy′=C(x)e∫−P(x)dx=C′(x)e∫−P(x)dx−C(x)P(x)e∫−P(x)dx
代入原方程 y ′ + P ( x ) y = Q ( x ) y{'}+P(x)y=Q(x) y′+P(x)y=Q(x) 中,得
C ′ ( x ) e ∫ − P ( x ) d x − C ( x ) P ( x ) e ∫ − P ( x ) d x + P ( x ) C ( x ) e ∫ − P ( x ) d x = Q ( x ) C ′ ( x ) e ∫ − P ( x ) d x = Q ( x ) C ′ ( x ) = Q ( x ) e ∫ P ( x ) d x \begin{aligned} C{'}(x)e^{\int_{}^{}{-P(x)dx}}-C(x)P(x)e^{\int_{}^{}{-P(x)dx}}+P(x)C(x)e^{\int_{}^{}{-P(x)dx}}&=Q(x) \\C{'}(x)e^{\int_{}^{}{-P(x)dx}}&=Q(x) \\C{'}(x)&=Q(x)e^{\int_{}^{}{P(x)dx}} \end{aligned} C′(x)e∫−P(x)dx−C(x)P(x)e∫−P(x)dx+P(x)C(x)e∫−P(x)dxC′(x)e∫−P(x)dxC′(x)=Q(x)=Q(x)=Q(x)e∫P(x)dx
两边积分,得
C ( x ) = ∫ Q ( x ) e ∫ P ( x ) d x + C 3 \begin{aligned} C(x)&={\int_{}^{}{Q(x)e^{\int_{}^{}{P(x)}}dx}}+C_3 \end{aligned} C(x)=∫Q(x)e∫P(x)dx+C3
③ 综合一阶齐次线性微分方程 y ′ + P ( x ) y = 0 y{'}+P(x)y=0 y′+P(x)y=0 的通解 y = C 1 e − ∫ P ( x ) d x y=C_1e^{-\int_{}^{}{P(x)dx}} y=C1e−∫P(x)dx
和一阶非齐次线性微分方程 y ′ + P ( x ) y = Q ( x ) y{'}+P(x)y=Q(x) y′+P(x)y=Q(x)的通解 y = C ( x ) e ∫ − P ( x ) d x y=C(x)e^{\int_{}^{}{-P(x)dx}} y=C(x)e∫−P(x)dx,
可得,方程 y ′ + P ( x ) y = Q ( x ) y{'}+P(x)y=Q(x) y′+P(x)y=Q(x) 的通解公式为
y = C 1 e − ∫ P ( x ) d x + C ( x ) e ∫ − P ( x ) d x y = e − ∫ P ( x ) d x [ C ( x ) + C 1 ] y = e − ∫ P ( x ) d x [ ∫ Q ( x ) e ∫ P ( x ) d x d x + C 3 + C 1 ] y = ( C 1 + C 3 ) e − ∫ P ( x ) d x + e − ∫ P ( x ) d x ∫ Q ( x ) e ∫ P ( x ) d x d x \begin{aligned} y&=C_1e^{-\int_{}^{}{P(x)dx}}+C(x)e^{\int_{}^{}{-P(x)dx}} \\y&=e^{-\int_{}^{}{P(x)dx}}[C(x)+C_1] \\y&=e^{-\int_{}^{}{P(x)dx}}[{\int_{}^{}{Q(x)e^{\int_{}^{}{P(x)dx}}dx}}+C_3+C_1] \\y&=(C_1+C_3)e^{-\int_{}^{}{P(x)dx}}+e^{-\int_{}^{}{P(x)dx}}{\int_{}^{}{Q(x)e^{\int_{}^{}{P(x)dx}}dx}} \end{aligned} yyyy=C1e−∫P(x)dx+C(x)e∫−P(x)dx=e−∫P(x)dx[C(x)+C1]=e−∫P(x)dx[∫Q(x)e∫P(x)dxdx+C3+C1]=(C1+C3)e−∫P(x)dx+e−∫P(x)dx∫Q(x)e∫P(x)dxdx
RC一阶低通滤波电路方程的推导
一阶线性微分方程的公式推导完毕,我们回到 RC一阶低通滤波电路方程
d u 0 d t + 1 R C u 0 = u i R C \begin{aligned} \\\frac{du_0}{dt}+\frac{1}{RC}u_0&=\frac{u_i}{RC} \end{aligned} dtdu0+RC1u0=RCui
由上文所推导的一阶线性微分方程的通解公式,可得
u 0 = C 0 e − ∫ 1 R C d t + e − ∫ 1 R C d t ( ∫ u i R C e ∫ 1 R C d t d t ) = C 0 e − t R C + e − t R C ( ∫ u i R C e t R C d t ) = C 0 e − t R C + e − t R C ( ∫ u i d e t R C ) \begin{aligned} u_0&=C_0e^{-\int_{}^{}{\frac{1}{RC}dt}}+e^{-\int_{}^{}{\frac{1}{RC}dt}}(\int_{}^{}{\frac{u_i}{RC}e^{\int_{}^{}{\frac{1}{RC}dt}}dt}) \\&=C_0e^{-\frac{t}{RC}}+e^{-\frac{t}{RC}}(\int_{}^{}{\frac{u_i}{RC}e^{\frac{t}{RC}}dt}) \\&=C_0e^{-\frac{t}{RC}}+e^{-\frac{t}{RC}}(\int_{}^{}{u_ide^{\frac{t}{RC}}}) \end{aligned} u0=C0e−∫RC1dt+e−∫RC1dt(∫RCuie∫RC1dtdt)=C0e−RCt+e−RCt(∫RCuieRCtdt)=C0e−RCt+e−RCt(∫uideRCt)
到这一步,需要用到分部积分法,即 ∫ u d v = u v − ∫ v d u \int_{}{}{udv}=uv-\int_{}{}{vdu} ∫udv=uv−∫vdu
这里我们分析RC滤波电路,是想分析电源上电的那一刻,RC电路的特性,所以 u i u_i ui 是阶跃信号,并且是单位阶跃函数,其表达式如下,
u i ( t ) = 0 , t < 0 u i ( t ) = 1 , t ≥ 0 \begin{aligned} u_i(t)&=0, \ \ t<0 \\u_i(t)&=1, \ \ t≥0 \end{aligned} ui(t)ui(t)=0, t<0=1, t≥0
其函数图象如下图所示,
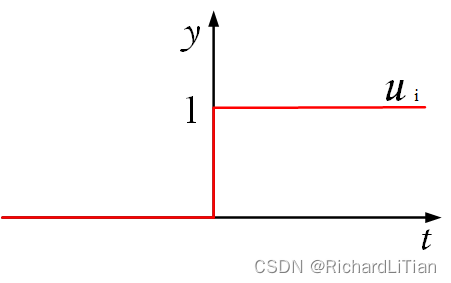
阶跃信号 u i u_i ui 的微分是冲激函数 δ i \delta_i δi ,如下图所示,
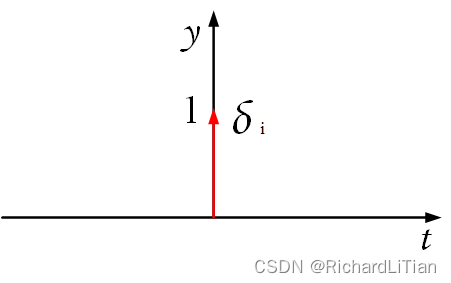
阶跃函数 u i u_i ui 与冲激函数 δ i \delta_i δi 有如下关系和性质:
∫ − ∞ t δ i ( τ ) d τ = u i ( t ) ∫ − ∞ + ∞ δ i ( t ) d t = 1 ∫ − 0 + 0 δ i ( t ) d t = 1 \begin{aligned} \int_{-\infty}^{t}{\delta_i(τ)}dτ&=u_i(t) \\\int_{-\infty}^{+\infty}{\delta_i(t)}dt&=1 \\\int_{-0}^{+0}{\delta_i(t)}dt&=1 \end{aligned} ∫−∞tδi(τ)dτ∫−∞+∞δi(t)dt∫−0+0δi(t)dt=ui(t)=1=1
所以,原函数可以继续往下推导如下
u 0 = C 0 e − t R C + e − t R C ( ∫ u i d e t R C ) = C 0 e − t R C + e − t R C [ u i e t R C − ∫ δ i ( t ) e t R C d t ] \begin{aligned} \\u_0&=C_0e^{-\frac{t}{RC}}+e^{-\frac{t}{RC}}(\int_{}^{}{u_ide^{\frac{t}{RC}}}) \\&=C_0e^{-\frac{t}{RC}}+e^{-\frac{t}{RC}}[u_ie^{\frac{t}{RC}}-\int_{}^{}{\delta_i(t)e^{\frac{t}{RC}}dt}] \end{aligned} u0=C0e−RCt+e−RCt(∫uideRCt)=C0e−RCt+e−RCt[uieRCt−∫δi(t)eRCtdt]
由阶跃信号的图象可知 u i u_i ui 在 t ≥ 0 t≥0 t≥0 的时候恒为1,在 t < 0 t<0 t<0 时恒为0,因为 R C RC RC 电路只在 t ≥ 0 t≥0 t≥0 时才有实际的物理意义,所以 u i e t R C = e t R C u_ie^{\frac{t}{RC}}=e^{\frac{t}{RC}} uieRCt=eRCt 。
对于冲激函数 δ i \delta_i δi 的积分,需要用到冲激函数的采样特性,如下: ∫ − ∞ + ∞ f ( t ) δ ( t ) d t = f ( 0 ) ∫ − ∞ + ∞ f ( t ) δ ( t − t 0 ) d t = f ( t 0 ) \begin{aligned} \int_{-\infty}^{+\infty}{f(t)\delta(t)}dt&=f(0) \\\int_{-\infty}^{+\infty}{f(t)\delta(t-t_0)}dt&=f(t_0) \end{aligned} ∫−∞+∞f(t)δ(t)dt∫−∞+∞f(t)δ(t−t0)dt=f(0)=f(t0)
所以 ∫ δ i ( t ) e t R C d t = e 0 R C d t = 1 \int_{}^{}{\delta_i(t)e^{\frac{t}{RC}}dt}=e^{\frac{0}{RC}}dt=1 ∫δi(t)eRCtdt=eRC0dt=1
所以,原函数可以继续往下推导如下
u 0 = C 0 e − t R C + e − t R C [ u i e t R C − ∫ δ i ( t ) e t R C d t ] = C 0 e − t R C + e − t R C ( e t R C − e 0 R C ) = C 0 e − t R C + 1 − e − t R C = ( C 0 − 1 ) e − t R C + 1 \begin{aligned} \\u_0&=C_0e^{-\frac{t}{RC}}+e^{-\frac{t}{RC}}[u_ie^{\frac{t}{RC}}-\int_{}^{}{\delta_i(t)e^{\frac{t}{RC}}dt}] \\&=C_0e^{-\frac{t}{RC}}+e^{-\frac{t}{RC}}(e^{\frac{t}{RC}}-e^{\frac{0}{RC}}) \\&=C_0e^{-\frac{t}{RC}}+1-e^{-\frac{t}{RC}} \\&=(C_0-1)e^{-\frac{t}{RC}}+1 \end{aligned} u0=C0e−RCt+e−RCt[uieRCt−∫δi(t)eRCtdt]=C0e−RCt+e−RCt(eRCt−eRC0)=C0e−RCt+1−e−RCt=(C0−1)e−RCt+1
推导到这一步,终于确定见到了 u 0 u_0 u0 与 R C RC RC 的函数关系的庐山真面目,但此时还有一个常数 C 0 C_0 C0 需要确定。这时就需要把初状态的值 t = 0 , u 0 = 0 t=0,u_0=0 t=0,u0=0 代入方程中,可得
u 0 = ( C 0 − 1 ) e − t R C + 1 0 = ( C 0 − 1 ) e − 0 R C + 1 0 = C 0 − 1 + 1 C 0 = 0 \begin{aligned} \\u_0&=(C_0-1)e^{-\frac{t}{RC}}+1 \\0&=(C_0-1)e^{-\frac{0}{RC}}+1 \\0&=C_0-1+1 \\C_0&=0 \end{aligned} u000C0=(C0−1)e−RCt+1=(C0−1)e−RC0+1=C0−1+1=0
所以,
u 0 = 1 − e − t R C \begin{aligned} \\u_0&=1-e^{-\frac{t}{RC}} \end{aligned} u0=1−e−RCt
这就是RC一阶低通电路的输出电压 u 0 u_0 u0 关于时间 t t t 的函数关系式。
Matlab 画出RC一阶低通滤波器的函数曲线
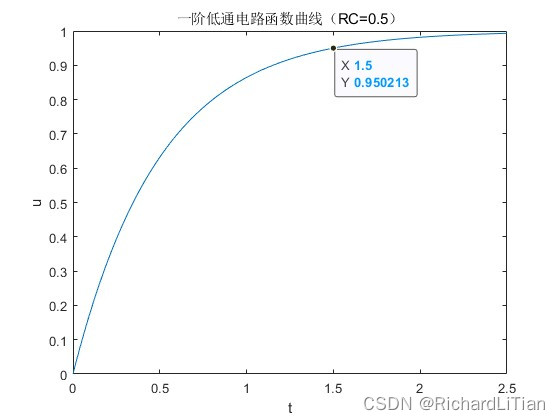
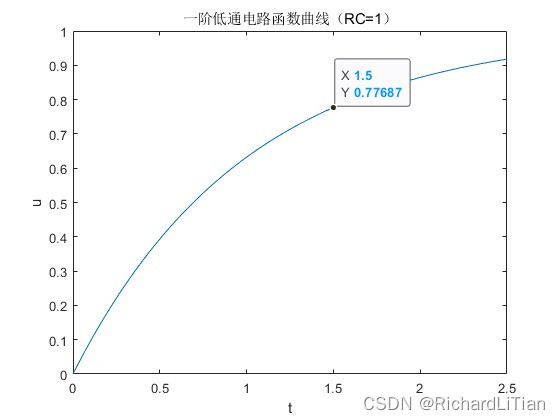
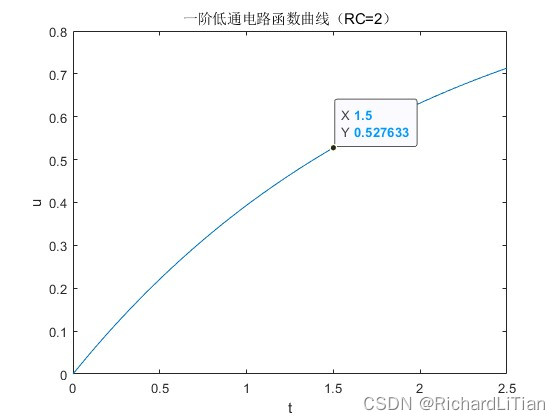
得到了RC一阶低通电路的输出电压 u 0 u_0 u0 关于时间 t t t 的函数关系式 u 0 = 1 − e − t R C u_0=1-e^{-\frac{t}{RC}} u0=1−e−RCt,对于式中的 R C RC RC ,可以分别取值0.5,1,2,我们将这三个函数的曲线分别画出来,得到下图,
matlab代码如下:
t = 0:0.01:2; % 定义x轴范围
u = 1-exp(-t/0.5); % 定义y轴范围
plot(t,u); % 画图
xlabel(‘t’); % x轴标签
ylabel(‘u’); % y轴标签
title(‘一阶低通电路函数曲线(RC=0.5)’); % 图片标题
yticks(0:0.1:2) %y轴刻度
由 u 0 = 1 − e − t R C u_0=1-e^{-\frac{t}{RC}} u0=1−e−RCt 的函数曲线可知,同样是在 t = 1.5 t=1.5 t=1.5 处取值, R C = 0.5 RC=0.5 RC=0.5 时, u = 0.95 u=0.95 u=0.95 ; R C = 1 RC=1 RC=1 时, u = 0.77 u=0.77 u=0.77 ; R C = 2 RC=2 RC=2 时, u = 0.52 u=0.52 u=0.52 。
由此可知,RC时间常数越小,则 u 0 u_0 u0 的上升时间就越短,也就是说 u 0 u_0 u0 能够更快地接近峰值 1。
RC时间常数的含义其实也很简单,就是当 t = R C t=RC t=RC 时, u 0 = 1 − e − t R C = 1 − e − 1 = 1 − 1 e = 1 − 0.3679 = 0.6321 V u_0=1-e^{-\frac{t}{RC}}=1-e^{-1}=1-\frac{1}{e}=1-0.3679=0.6321V u0=1−e−RCt=1−e−1=1−e1=1−0.3679=0.6321V, u 0 u_0 u0 从 0 V 0V 0V 上升到 0.6321 V 0.6321V 0.6321V 或是从 0 V 0V 0V 上升到电源电压的 63.21 % 63.21\% 63.21% 所用的时间就是时间常数 R C RC RC 的值,因为不同的电路 R C RC RC 的值不同,所以会导致从 0 V 0V 0V 上升到电源电压的 63.21 % 63.21\% 63.21% 所用的时间也不尽相同。
Modelsim 仿真
Modelsim仿真电路图如下图所示,我们选用 R = 1 k Ω , C = 1 μ F R=1kΩ,C=1μF R=1kΩ,C=1μF,则 R C = 1 k × 1 μ ∙ s = 1 m s RC=1k×1μ\bullet s=1ms RC=1k×1μ∙s=1ms 。
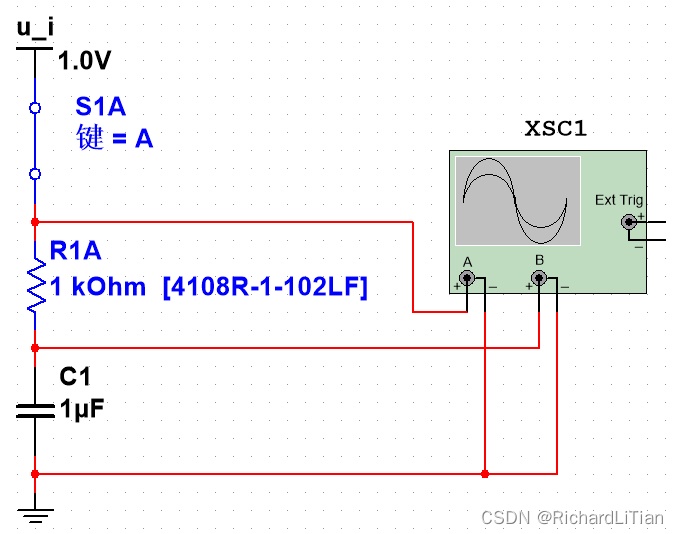
示波器波形图如下,
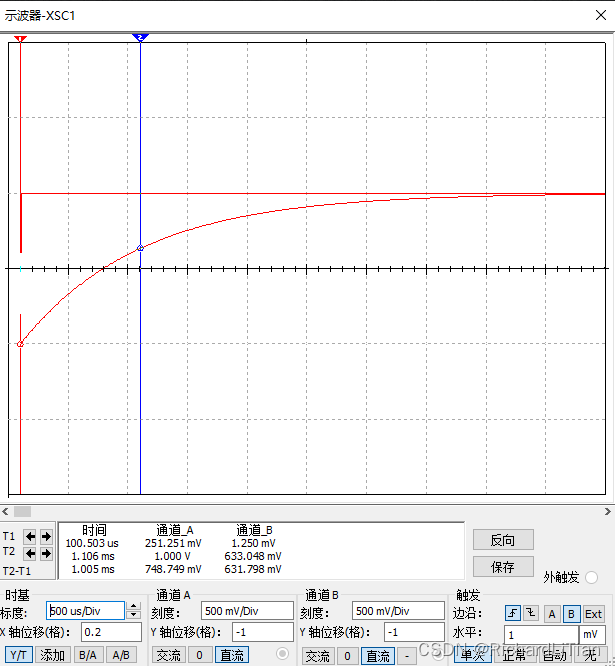
由波形图实测可得, u 0 u_0 u0 从 1.25 m V 1.25mV 1.25mV 上升到 633.048 m V 633.048mV 633.048mV 用时 1.005 m s 1.005ms 1.005ms ,符合时间常数 R C RC RC 的计算值。
我们也可以用Matlab再画一条 R C = 1 m s RC=1ms RC=1ms 的函数曲线,代码如下:
t = 0:0.0001:0.002; % 定义x轴范围
u = 1-exp(-t/0.001); % 定义y轴范围
plot(t,u); % 画图
xlabel(‘t’); % x轴标签
ylabel(‘u’); % y轴标签
title(‘一阶低通电路函数曲线(RC=1ms)’); % 图片标题
yticks(0:0.1:2)
曲线图如下,
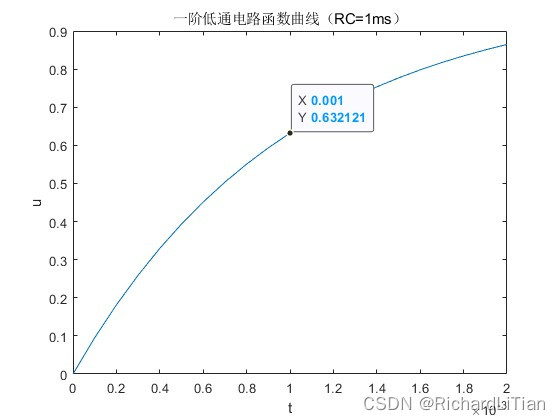
由曲线图也可得到,当 u 0 = 0.6321 V u_0=0.6321V u0=0.6321V 时, t = 0.001 s = 1 m s t=0.001s=1ms t=0.001s=1ms,符合计算值。
总结
至此,我们对 R C RC RC 一阶低通滤波器电路完成了数学推导和电路仿真,这其中包含有一阶线性微分方程的求解、电路原理的运用以及仿真工具的使用。 R C RC RC 电路的运用非常广泛,在电路中的作用也非常重要,在分析 R C RC RC 电路时,从原理上分析更有助于我们理解电路,进而改善和提升电路的性能。
这篇关于一阶RC低通滤波电路推演与仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








