运算放大器(运放)低通滤波反相放大器电路和积分器电路

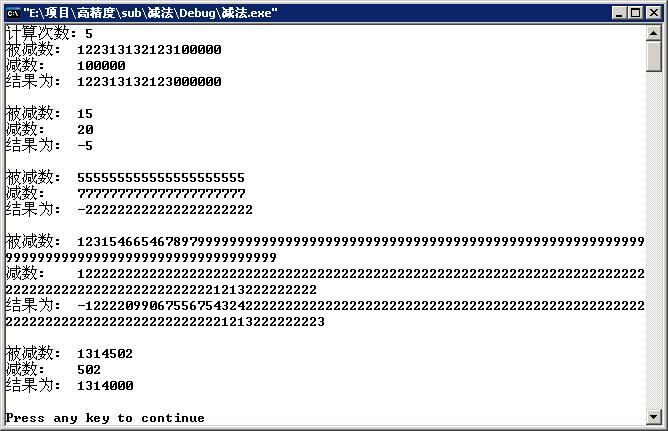
本文主要是介绍运算放大器(运放)低通滤波反相放大器电路和积分器电路，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

低通滤波反相放大器电路

运放积分器电路请访问下行链接
运算放大器(运放)积分器电路

设计目标

输入ViMin	输入ViMax	输出VoMin	输出VoMax	BW：fp	电源Vee	电源Vcc
–0.1V	0.1V	–2V	2V	2kHz	–2.5V	2.5V

设计说明

这款可调式低通反相放大器电路可将信号电平放大 26dB 或 20V/V。R2 和 C1 可设置此电路的截止频率。此电路的频率响应与无源 RC 滤波器的相同，除非输出按放大器的通带增益进行放大。低通滤波器通常用于音频信号链，此滤波器有时也称为低音增强滤波器。

低通滤波反相放大器电路，和下图区别，主要在于R2取值较小，使工作状态不同，和运放积分电路相似

运算放大器(运放)积分器电路，和上图区别，主要在于R2取值较大，致使信号主要从电容通过

设计说明

1. C1 和 R2 可设置低通滤波器截止频率。
2. 共模电压根据运算放大器的同相输入设置，在这种情况下，输入为 1/2 Vs。
3. 使用高值电阻器可能会减小电路的相位裕度并在电路中引入额外的噪声。
4. R2 和 R1 可设置电路增益。
5. 为音频低音增强应用选择 2kHz 的极点频率 fp。
6. 避免将电容负载直接放置在放大器的输出，从而更大限度减少稳定性问题。
7. 大信号性能可能会受到压摆率的限制。因此，应检查数据表中的最大输出摆幅与频率间的关系图，从而更大限度减小转换导致的失真。
8. 有关运算放大器线性运行区域、稳定性、转换导致的失真、电容负载驱动、驱动 ADC 和带宽的更多信息，请参阅“设计参考”部分。

设计步骤

下面给出了该电路的直流传递函数。
$$Vo=Vi\times (-\frac{R2}{R1})$$

1. 为给定的通带增益选择电阻值。
   $$Gain=\frac{R_2}{R_1}=20\frac{V}{V}(26dB)$$
   $$R_1=1k\Omega$$
   $$R_2=Gain\times (R_1)=20\frac{V}{V}\times 1k\Omega =20k\Omega$$
2. 选择低通滤波器极点频率 fp。
   $$f_p=2kHz$$
3. 使用 R2 设置 fp 的位置，计算 C1。
   $$f_p=\frac{1}{2\times \pi \times R_2\times C_1}=2kHz$$
   $$C_1=\frac{1}{2\times \pi \times R_2\times f_p}=\frac{1}{2\times \pi \times 20K\Omega \times 2Khz}=3.98nF\approx 3.9nF(StandardValue)$$
4. 计算更大限度降低转换导致的失真所需的最小压摆率。
   $$V_p=\frac{SR}{2\times \pi \times f_p}\to SR>2\times \pi \times f_p\times V_p$$
   $$SR>2\times \pi \times 2kHz\times 2V=0.025\frac{V}{us}$$
5. $S{R}_{TLV9002}=2V/\mu s$，因此它满足该要求

设计仿真

交流仿真结果

交流仿真结果

瞬态仿真结果

100Hz、0.2Vpp 的正弦波可产生 4Vpp 的输出正弦波。

100Hz、0.2Vpp 的正弦波可产生 4Vpp 的输出正弦波

100kHz、0.2Vpp 的正弦波可产生 0.1Vpp 的输出正弦波。

100kHz、0.2Vpp 的正弦波可产生 0.1Vpp 的输出正弦波。

设计采用的运算放大器TLV9002

Vss	1.8V 至 5.5V
VinCM	轨到轨
Vout	轨到轨
Vos	0.4mV
Iq	60µA
Ib	5pA
UGBW	1MHz
SR	2V/µs
通道数	1、2、4

设计备选运算放大器OPA375

Vss	2.25V 至 5.5V
VinCM	Vee 至 Vcc –1.2V
Vout	轨到轨
Vos	0.15mV
Iq	890µA
Ib	10pA
UGBW	10MHz
SR	4.75V/µs
通道数	1

这篇关于运算放大器(运放)低通滤波反相放大器电路和积分器电路的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---