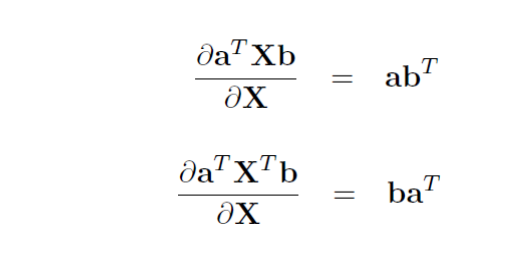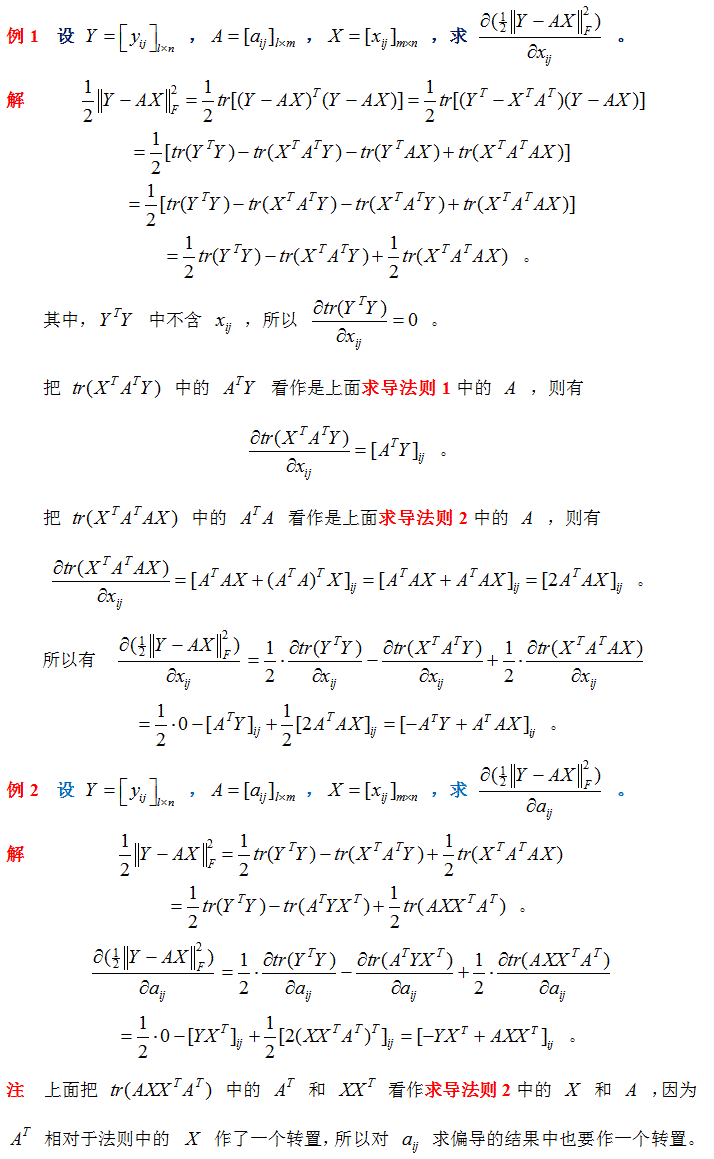范数专题
python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)(向量的第二范数为传统意义上的向量长度),(如何求取向量的单位向量)
转载自: https://www.cnblogs.com/devilmaycry812839668/p/9352814.html 求取向量二范数,并求取单位向量(行向量计算) import numpy as npx=np.array([[0, 3, 4], [2, 6, 4]])y=np.linalg.norm(x, axis=1, keepdims=True)z=x/y x 为需
【转】常见向量范数和矩阵范数
1、向量范数 1-范数:,即向量元素绝对值之和,matlab调用函数norm(x, 1) 。 2-范数:,Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方,matlab调用函数norm(x, 2)。 ∞-范数:,即所有向量元素绝对值中的最大值,matlab调用函数norm(x, inf)。 -∞-范数:,即所有向量元素绝对值中的最小值,matlab调用函数nor
线性方程求解之 二范数类型
求解线性系统 在线性代数中我们经常需要求解具有m个方程 ,n 个 未知量的问题。这个问题可以以简洁的形式 表示为 Ax=b Ax=b 其中 A A 是一个m×nm\times n , x x是一个长度为n的向量(如不特别强调,都是列向量) ,bb是一个长度为m 的向量。如果 m=n m = n ,并且 满秩(各行向量或列向量线性无关) ,则这个线性方程的解为 x=A−1b x=A^{
线性代数|机器学习-P9向量和矩阵范数
文章目录 1. 向量范数2. 对称矩阵S的v范数3. 最小二乘法4. 矩阵范数 1. 向量范数 范数存在的意义是为了实现比较距离,比如,在一维实数集合中,我们随便取两个点4和9,我们知道9比4大,但是到了二维实数空间中,取两点A(1,0),B(3,4),这时候我们就没办法比较它们之间的大小了,因为它们不是可以比较的实数,于是我们引入了范数这个概念,把我们的A,B两个点变成 ∣ ∣
矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A = \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\v
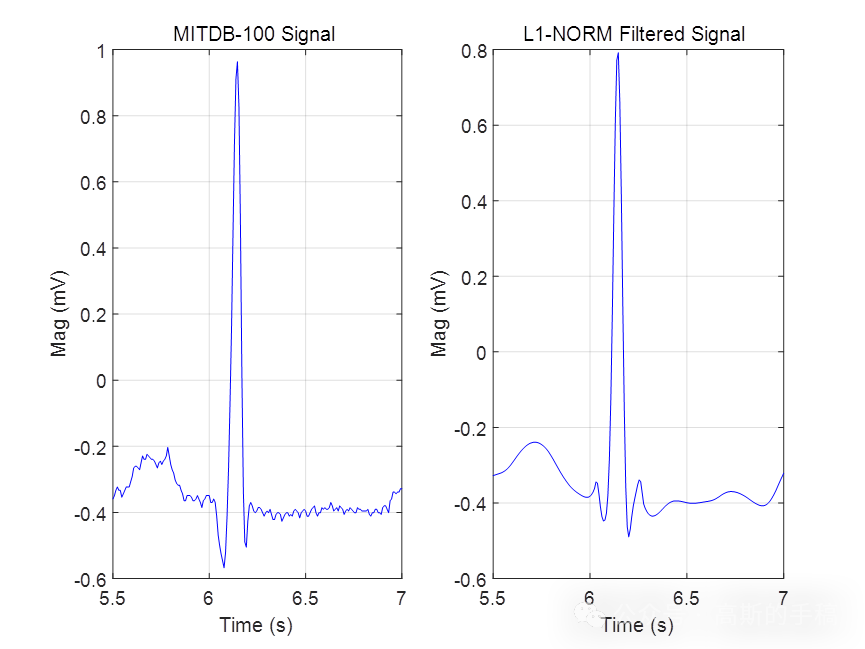
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一定范围内是发散的,而L1范数正则化方法的解通常是稀疏的。 鉴于此,采用L1范数惩罚的稀疏正则化最小二乘方法对心电信号进行降噪,算法可迁移至金融时间序列,地震信号
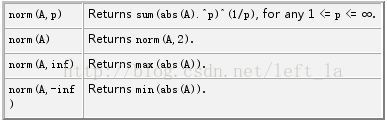
(转载)matlab中各种范数求解norm
原文http://blog.csdn.net/yihaizhiyan/article/details/6904599 %X为向量,求欧几里德范数,即 。 n = norm(X,inf) %求 无穷-范数,即 。 n = norm(X,1) %求1-范数,即 。 n = norm(X,-inf) %求向量X的元素的绝对值的最小值,即 。 n = norm(X, p) %求p-范数,即 ,所以no
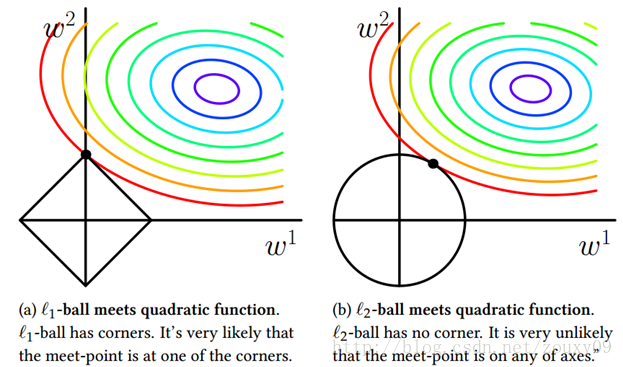
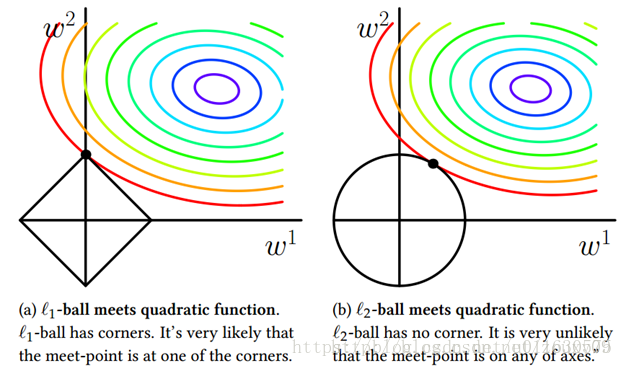
LASSO与redge回归区别 L1 L2范数之间的区别
转载自:http://blog.csdn.net/sinat_26917383/article/details/52092040 一、正则化背景 监督机器学习问题无非就是“minimizeyour error while regularizing your parameters”,也就是在规则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据, 而规
矩阵的 Frobenius 范数及其求偏导法则
矩阵的迹求导法则 1. 复杂矩阵问题求导方法:可以从小到大,从scalar到vector再到matrix 2. x is a column vector, A is a matrix d(A∗x)/dx=A d(A*x)/dx=A d(xT∗A)/dxT=A d(x^T*A)/dx^T=A d(xT∗A)/dx=AT d(x^T*A)/dx=A^T d(xT
对抗攻击笔记03:l0,l2,l∞范数
攻击成功率只能从一定程度表明对抗样本的质量,工程和科研中还需要使用更多的指标来量化对抗样本的质量,其中最常用的是扰动的l0和l2范数 l0范数 l0范数是指向量中非0的元素的个数,因此扰动的lo范数指的是扰动的非0的元素的个数。以图像数据为例,针对图像数据的扰动的l0范数指的就是修改的像素数据个数。 扰动量可以表示为: #计算改变量deta=img[0]-img_adv[0] 扰动的
[机器学习] 第一章 绪论 2.L0、L1、L2 范数正则化
参考:深度学习正则化-参数范数惩罚(L1,L2范数)_wangheng673的博客-CSDN博客 参考:贝叶斯角度看 L1 & L2 正则化 | Wei's Blog 目录
关于向量的模和向量的范数的理解
向量的模 含义 向量 的长度叫做向量的模,记作 ,也就是向量 的大小 计算公式 对于向量 属于n维复向量空间 =(x1,x2,…,xn) 的模为 = 向量的范数 范数,在机器学习中通常用于衡量一个向量的大小,形式上, 范数的定义如下:
矩阵的范数:L0范数、L1范数、L2范数、P范数(双竖线有下标)
范数(norm)是数学中的一种基本概念。在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即 ①非负性;②齐次性;③三角不等式。它常常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。 设有矩阵 L0范数: 矩阵中非0元素的个数,则 L1范数:矩阵中每个元素的绝对值之和,则 L2范数:矩阵中每个元素的平方和的平方根,也可理解为一个大向量的欧式距离,则 P范数:矩阵中
三维网格去噪算法(L0范数最小化,包含二维图像去噪)
参考文章(技术来源):Mesh denoising via L0 minimization 上面参考文章提出了一种基于L0范数最小化的三角网格去噪算法。该思想由二维图像平滑引申而来,所以先从基于L0范数最小化的二维图像平滑的原理入手,来一步步讲解。 一. 基于L0范数最小化的二维图像平滑 1. 目的 (1) 去噪后得到的输出(out)图像尽可能接近原图(不要损失边缘,纹理等细节信息);
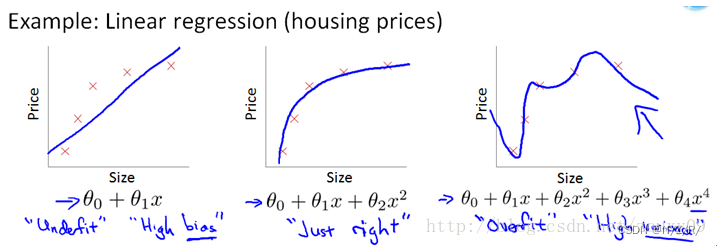
机器学习(深度学习)缓解过拟合的方法——正则化及L1L2范数详解
机器学习(深度学习)缓解过拟合的方法——正则化 L1范数和L2范数L1范数L2范数 过拟合的本质:模型对于噪声过于敏感,把训练样本里的噪声当做特征进行学习,以至于在测试集的表现不好,加入正则化后,当输入有轻微的改动,结果受到的影响较小。 正则化的方法主要有以下几种: 参数范数惩罚,比较好理解,将范数加入目标函数(损失函数),常见的有一范数,二范数数据集增强添加噪声ear
机器学习中的正则化和范数规则化
正则化和范数规则化 文章安排:文章先介绍了正则化的定义,然后介绍其在机器学习中的规则化应用L0、L1、L2规则化范数和核范数规则化,最后介绍规则化项参数的选择问题。 正则化(regularization)来源于线性代数理论中的不适定问题,求解不适定问题的普遍方法是:用一族与原不适定问题相“邻近”的适定问题的解去逼近原问题的解,这种方法称为正则化方法。如何建立有效的正则化方法是反问题领域中不适定
重磅独家 | 腾讯AI Lab AAAI18现场陈述论文:用随机象限性消极下降算法训练L1范数约束模型
前言:腾讯 AI Lab共有12篇论文入选在美国新奥尔良举行的国际人工智能领域顶级学术会议 AAAI 2018。腾讯技术工程官方号独家编译了论文《用随机象限性消极下降算法训练L1范数约束模型》(Training L1-Regularized Models with Orthant-Wise Passive Descent Algorithms),该论文被 AAAI 2018录用为现场陈
机器学习中的范数规则化之 L0、L1与L2范数
原文:https://blog.csdn.net/zouxy09/article/details/2497199 今天我们聊聊机器学习中出现的非常频繁的问题:过拟合与规则化。我们先简单的来理解下常用的L0、L1、L2和核范数规则化。最后聊下规则化项参数的选择问题。这里因为篇幅比较庞大,为了不吓到大家,我将这个五个部分分成两篇博文。知识有限,以下都是我一些浅显的看法,如果理解存
弗罗贝尼乌斯范数 matlab,Matlab求范数
对 p = 2,这称为弗罗贝尼乌斯范数(Frobenius norm)或希尔伯特-施密特范数( Hilbert–Schmidt norm),不过后面这个术语通常只用于希尔伯特空间。这个范数可用不同的方式定义: 这里 A* 表示 A 的共轭转置,σi 是 A 的奇异值,并使用了迹函数。弗罗贝尼乌斯范数与 Kn 上欧几里得范数非常类似,来自所有矩阵的空间上一个内积。 弗罗贝尼乌斯范范数是服从乘法的
【机器学习】范数规则化之——L0、L1与L2范数
【机器学习】范数规则化之——L0、L1与L2范数 在机器学习领域中,我们通常求解模型的目标是“minimizeyour error while regularizing your parameters”,也就是在规则化参数的同时最小化误差。 最小化误差是为了让我们的模型拟合我们的训练数据,而规则化参数是防止我们的模型过分拟合我们的训练数据。因为参数太多,会导致我们的模型复杂度上升,容易过拟合,
0范数,1范数,欧几里得范数等范数总结
以下分别列举常用的向量范数和矩阵范数的定义。 向量范数 1-范数: 即向量元素绝对值之和,matlab调用函数norm(x, 1) 。 2-范数: Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方,matlab调用函数norm(x, 2)。 范数: 即所有向量元素绝对值中的最大值,matlab调用函数norm(x, inf)。 范数
向量范数+不同范数之间的关系
近期公式证明时候遇到向量范数的运算性质,略作整理: 向量范数 Def. 设 V V是Ω\Omega上的线性空间, α∈V \alpha \in V , || α \alpha||: V→R+ V \rightarrow R_+, 满足 非负性齐次性 ||kα||=|k|⋅||α||,∀k∈Ω ||k\alpha||=|k| \cdot ||\alpha||,\forall k
.norm() 范数
(A- B).norm().item() 是默认计算A与B的第二范数,如果你想计算差向量的第一范数(也称为L1范数),可以在norm()方法中传递p=1参数,这样就会计算出L1范数。例如: (A- B).norm(p=1).item() 其中,使用.item()方法将结果转换为Python的标量(scalar)类型