【机器学习】范数规则化之—

本文主要是介绍【机器学习】范数规则化之——L0、L1与L2范数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【机器学习】范数规则化之——L0、L1与L2范数

在机器学习领域中，我们通常求解模型的目标是“minimizeyour error while regularizing your parameters”，也就是在规则化参数的同时最小化误差。

最小化误差是为了让我们的模型拟合我们的训练数据，而规则化参数是防止我们的模型过分拟合我们的训练数据。因为参数太多，会导致我们的模型复杂度上升，容易过拟合，也就是我们的训练误差会很小。

但训练误差小并不是我们的最终目标，我们的目标是希望模型的测试误差小，也就是能准确的预测新的样本。所以，我们需要保证模型“简单”的基础上最小化训练误差，这样得到的参数才具有好的泛化性能（也就是测试误差也小），而模型“简单”就是通过规则函数来实现的。

另外，规则项的使用还可以约束我们的模型的特性。这样就可以将人对这个模型的先验知识融入到模型的学习当中，强行地让学习到的模型具有人想要的特性，例如稀疏、低秩、平滑等等。

1、监督学习

一般来说，监督学习可以看做最小化下面的目标函数：
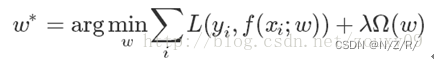
在这里插入图片描述
其中，第一项 $L(y_i,f(x_i;w))$ 衡量我们的模型（分类或者回归）对第 $i$ 个样本的预测值
$f(x_i;w)$ 和真实的标签 $y_i$ 之前的误差。因为我们的模型是要拟合我们的训练样本的嘛，所以我们要求这一项最小，也就是要求我们的模型尽量的拟合我们的训练数据。但正如上面说言，我们不仅要保证训练误差最小，我们更希望我们的模型测试误差小，所以我们需要加上第二项，也就是对参数 $w$ 的规则化函数 $Ω (w)$ 去约束我们的模型尽量的简单。

规则化函数 $Ω (w)$ 也有很多种选择，一般是模型复杂度的单调递增函数，模型越复杂，规则化值就越大。比如，规则化项可以是模型参数向量的范数。然而，不同的选择对参数 $w$ 的约束不同，取得的效果也不同，但我们在论文中常见的都聚集在：零范数、一范数、二范数、迹范数、Frobenius范数和核范数等等。

2、L0范数与L1范数

L0范数是指向量中非0的元素的个数。 如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0。

L1范数是指向量中各个元素绝对值之和， 也有个美称叫“稀疏规则算子”（Lasso regularization）。

L1范数和L0范数可以实现稀疏，L1因具有比L0更好的优化求解特性而被广泛应用。

为什么要稀疏？让我们的参数稀疏有什么好处呢？这里扯两点：

1）特征选择(Feature Selection)：

大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，xi的大部分元素（也就是特征）都是和最终的输出yi没有关系或者不提供任何信息的，在最小化目标函数的时候考虑xi这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。

2）可解释性(Interpretability)：

另一个青睐于稀疏的理由是，模型更容易解释。例如患某种病的概率是y，然后我们收集到的数据x是1000维的，也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型：y=w1x1+w2x2+…+w1000x1000+b（当然了，为了让y限定在[0,1]的范围，一般还得加个Logistic函数）。通过学习，如果最后学习到的w就只有很少的非零元素，例如只有5个非零的wi，那么我们就有理由相信，这些对应的特征在患病分析上面提供的信息是巨大的，决策性的。也就是说，患不患这种病只和这5个因素有关，那医生就好分析多了。但如果1000个wi都非0，医生面对这1000种因素，累觉不爱。

3、L2范数

除了L1范数，还有一种更受宠幸的规则化范数是L2范数: ||W||2。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫“岭回归”（Ridge Regression），有人也叫它“权值衰减weight decay”。这用的很多吧，因为它的强大功效是改善机器学习里面一个非常重要的问题：过拟合。
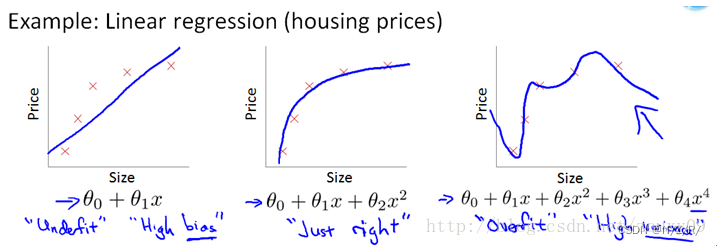
在这里插入图片描述
L2范数是指向量各元素的平方和然后求平方根。 我们让L2范数的规则项||W||2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的哦。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。