本文主要是介绍【转】常见向量范数和矩阵范数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、向量范数
1-范数: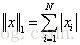
2-范数: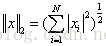
∞-范数: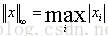
-∞-范数: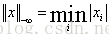
p-范数: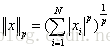
2、矩阵范数
1-范数: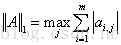
2-范数: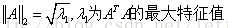
∞-范数: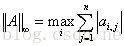
F-范数: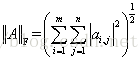
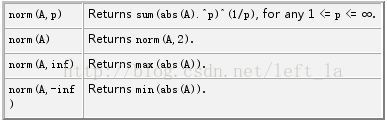
附matlab中norm函数说明
The norm of a matrix is a scalar that gives some measure of the magnitude of the elements of the matrix. The norm function calculates several different types of matrix norms:
n = norm(A) returns the largest singular value of A, max(svd(A)).
n = norm(A,p) returns a different kind of norm, depending on the value of p.
When A is a vector:
这篇关于【转】常见向量范数和矩阵范数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!