矩阵的范数：L0范数、L1范数、L2范数、P范数（双竖线有下标）

本文主要是介绍矩阵的范数：L0范数、L1范数、L2范数、P范数（双竖线有下标），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

范数(norm)是数学中的一种基本概念。在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即

①非负性；②齐次性；③三角不等式。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。

设有矩阵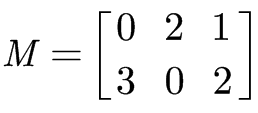 

L0范数： 矩阵中非0元素的个数，则

L1范数：矩阵中每个元素的绝对值之和，则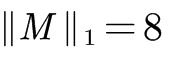

L2范数：矩阵中每个元素的平方和的平方根，也可理解为一个大向量的欧式距离，则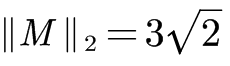

---

P范数：矩阵中每个元素的绝对值的p次幂之和的p次根，实际上P范数是L0,1,2范数的一种推广，或者说Lx范数是P范数在p=x时的情况，则有 

这篇关于矩阵的范数：L0范数、L1范数、L2范数、P范数（双竖线有下标）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---