0范数，1范数，欧几里得范数等范数总结

本文主要是介绍0范数，1范数，欧几里得范数等范数总结，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

以下分别列举常用的向量范数和矩阵范数的定义。

• 向量范数

1-范数：

即向量元素绝对值之和，matlab调用函数norm(x, 1) 。

2-范数：

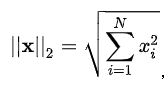
Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

范数：

即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

范数

，即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

p-范数

，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

 

• 矩阵范数

1-范数：

， 列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A, 1)。

 

2-范数：

，为的最大特征值，

，谱范数，即A'A矩阵的最大特征值的开平方。matlab调用函数norm(x, 2)。
范数：

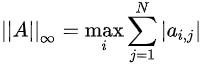
，行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A, inf)。

F-范数：

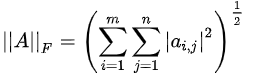
，Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A, ’fro‘)。

核范数：

      ，是A的奇异值。

即奇异值之和。

这篇关于0范数，1范数，欧几里得范数等范数总结的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---