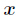欧几里得专题
【洛谷P2054洗牌】AC代码(扩展欧几里得+二分快速幂+二分龟速乘)
题目描述 题目链接 为了表彰小联为Samuel星球的探险所做出的贡献，小联被邀请参加Samuel星球近距离载人探险活动。 由于Samuel星球相当遥远，科学家们要在飞船中度过相当长的一段时间，小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后，大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。 对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数
扩展欧几里得算法——AcWing.877扩展欧几里得算法
扩展欧几里得算法 定义 扩展欧几里得算法是用来在已知整数 a、b 的情况下，求解一组整数 x、y 使得 ax + by = gcd(a, b)（gcd 表示最大公约数）。 运用情况 求解线性同余方程。在密码学等领域有广泛应用。 注意事项 要注意边界情况和特殊值的处理。在计算过程中要注意数据的范围，避免溢出。 解题思路 通过递归的方式不断缩小问题规模。从较大的数对(a, b)逐步递推
poj 1061 数论 扩展欧几里得算法
题目还算简单，但是得用long long #include<cstdio>#define size_num 51000#include<cstring>#include<iostream>using namespace std;void exgcd(long long a,long long b,long long &d,long long &x,long long& y){if
POJ - 1061 青蛙的约会 （扩展欧几里得算法）
Description 两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰
uva 10548 - Find the Right Changes(拓展欧几里得)
题目链接：uva 10548 - Find the Right Changes 题目大意：给定A，B，C，求x，y，使得xA+yB=C，求有多少种解。 解题思路：拓展欧几里得，保证x，y均大于等于0，确定通解中t的取值。 #include <cstdio>#include <cstring>#include <cmath>#include <algorithm>using nam
uva 10413 - Crazy Savages(拓展欧几里得)
题目链接：uva 10413 - Crazy Savages 题目大意：一座山有m个山洞，形成一个圈，现在有n个部落的人，每个部落一开始住在ci山洞，第2天会向后面移动pi个位置，一共会在这座山住li天。现在如果两个部落在同一个山洞相遇，则会发生战争，问说m最小时多少的时候，保证不会发生争斗。 解题思路:因为每个部落都有自己的存在时间，所以枚举m，然后枚举两个部落，判断他们有没有可能相遇
欧几里得数据和非欧几里得数据
欧几里德数据：数据特点是排列整齐。对于某个节点，很容易可以找出其邻居节点，就在旁边，不偏不倚。最常见到的是图片(image)和视频(video)以及语音(voice)。 非欧几里德数据：排列不整齐，比较的随意。具体体现在：对于数据中的某个点，难以定义出其邻居节点出来，或者是不同节点的邻居节点的数量是不同的。
SGU 106 The equation(拓展欧几里得)
通解形式 然后利用x，y去求出范围，就能得到解的个数 注意特判a和b都为0的情况 代码： #include <cstdio>#include <cstring>#include <cmath>#include <algorithm>using namespace std;typedef long long ll;ll a, b, c;double a1, a2, b1
欧几里得算法求最大公约数的递归和非递归实现
在数学中，欧几里得算法，又称辗转相除法，是求最大公约数（greatest common divisor）的算法。辗转相除法首次出现于欧几里得的《几何原本》（第VII卷，命题i和ii）中，而在中国则可以追溯至东汉出现的《九章算术》。 两个整数的最大公约数是能够同时整除它们的最大的正整数。 辗转相除法基于如下原理：两个整数的最大公约数等于其中较小的数和两数的差的最大公约数。例如，252和105的最
nyoj-Color the necklace（Ploya定理 + 欧拉函数 + 扩展欧几里得（求逆元））
题目链接：http://acm.nyist.net/JudgeOnline/problem.php?pid=688 此题题解 不太懂，因为对这些概念，定理太模糊，理解起来比较困难，不过想想还是应该把代码写出来； 题意：给你一个数 n ，代表 n 种颜色和n个珠子，问你可以组合多少种长度为n的项链；不需要用掉n种颜色，项链的旋转和翻转都是为同一条 题解： http://pan.baidu
数论基础题目八题【欧几里得】【筛法素数】【中国剩余定理】
之前看的数论的知识，现在做几道题目找找感觉..... poj 1061 传送门 题目大意，给你x，y，m，n，L。代表青蛙a的坐标x，青蛙b的坐标y，青蛙a一次跳的距离m，青蛙b一次跳的距离n，以及mod的值L，求经过多少次跳相遇。即求：(m-n)*x0=(x-y)(mod L); 模线性方程的解，不过要注意处理，因为(m-n)和(x-y)有可能是负的，如果(m-n)是负的，则直接对
UVALive 6428 A+B 【扩展欧几里得】
题目链接：https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4439 题目大意：给出a，b，S三个数，每次可以选择从a的位置加到b上，也可以从b的位置加到a上，问a或者b的位置上能否达到S。 比如：给出a和b，可以得到的是
POJ 2115 C Looooops 模线性方程（扩展欧几里得）
题解：转换一下。和青蛙那题差不多。 #include<iostream>#include<cmath>using namespace std;__int64 Egcd ( __int64 a, __int64 b, __int64 &x, __int64 &y ){__int64 tmp, ret;if ( b == 0 ){x = 1, b = 0;return a;}ret = E
POJ 2142 The Balance 扩展欧几里得，求|x|+|y|最小
题解：先做出两个函数的图像，然后求|x|+|y|的最小值。|x|+|y|=|x0+b/d *t |+|y0-a/d *t| 这个关于t的函数的最小值应该在t零点附近（在斜率大的那条折线的零点附近，可以观察出来）。以下三种情况中，函数最小值都应该出现在B点附近。 #include<cstdio>#include<algorithm>using std::swap;int
POJ 1006 Biorhythms 中国剩余定理/扩展欧几里得
先看视频：http://v.youku.com/v_show/id_XMTExNTAzOTIw.html #include<cstdio>int main(){int p, e, i, d;int num, cnt = 1;while ( scanf("%d%d%d%d",&p,&e,&i,&d) ){if ( d == -1 ) break;num = (5544*p + 14421*
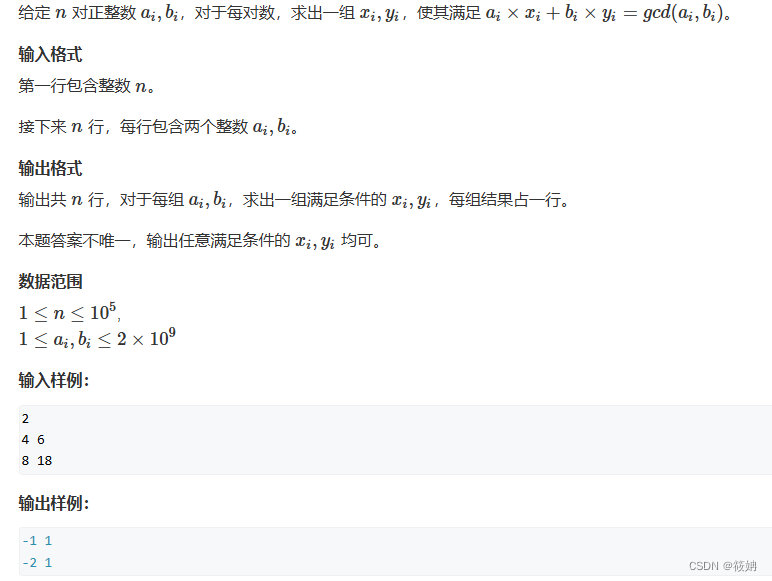
牛客-小乐乐与欧几里得
目录 题目 描述 输入描述： 输出描述： 示例1 示例2 解题 题目 描述 小乐乐最近在课上学习了如何求两个正整数的最大公约数与最小公倍数，但是他竟然不会求两个正整数的最大公约数与最小公倍数之和，请你帮助他解决这个问题。 输入描述： 每组输入包含两个正整数n和m。(1 ≤ n ≤ 109，1 ≤ m ≤ 109) 输出描述： 对于每组输入，输出一个正整数，为n和m的最大
牛客网暑期ACM多校训练营（第十场）Rikka with Ants(类欧几里得)
题目链接：https://www.nowcoder.com/acm/contest/148/H 题目大意：有两只蚂蚁从(1,0)点出发往上走，但是一只不能越过，一只不能越过，如果不能往上了就往右边一格(移动的距离一定是整数)，问这两只蚂蚁的行走路线里有多少个整点重合。 题目思路：针对一条线来说，我们可以针对蚂蚁走的点得到两个约束条件，第一个就是蚂蚁不能越过线，拿做例子，那么，还有一
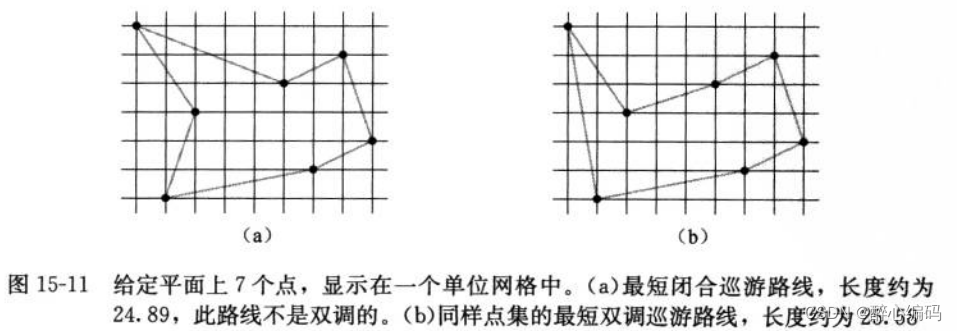
双调欧几里得旅行商问题的最优算法设计与实现
一、背景 双调欧几里得旅行商问题（Double Bitonic TSP）是欧几里得旅行商问题（Euclidean TSP）的一个特殊版本。在标准的欧几里得旅行商问题中，我们需要找到一条最短的路径，这条路径要求访问者从一个城市出发，经过所有其他城市恰好一次，最后返回到起始城市。这个问题是非常复杂的，尤其是当城市数量很多时，可能的路径组合数量是巨大的，因此很难快速找到一个最优解。 而双调欧几里得旅
Sweet Snippet 系列之 扩展欧几里得算法
扩展欧几里得算法的简单实现 扩展欧几里得算法是欧几里得算法(辗转相除法)的扩展,欧几里得算法可以用于求解两个自然数(记为 a a a 和 b b b)的最大公约数,而扩展欧几里得算法不仅可以求出 a a a 和 b b b 的最大公约数,还能同时计算出两个整数 x x x 和 y y y, 使它们满足等式(等式中的 g c d ( a , b ) gcd(a, b) gcd(
UVALive6428 A+B【扩展欧几里得算法+GCD】
Regionals 2013 >> Europe - Southeastern 问题链接：UVALive6428 A+B。 问题分析： 可以看作是解方程ax+by=s的问题。 先用扩展欧几里德算法进行计算，求得ax+by=gcd(a,b)=d。若s%d!=0，则无解。 若有解，再进行迭代计算求得最小非负解。 另外一个关键的地方在于需要考虑a,b和s为0的情形。 程序说明：（略）
数论常用内容——欧几里得算法与扩展欧几里得算法
欧几里得算法 欧几里得算法有一个为更多人所知的名字叫“辗转相除法”，它是用来求解两个数的最大公约数的算法 其计算原理依赖于下面的定理： 定理：两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。最大公约数（greatest common divisor）缩写为gcd。即：gcd(a,b) = gcd(b,a mod b) (不妨设a>b 且r=a mod b ,r不为0)
COCI HASH —— 扩展欧几里得
应该能进 题意： 定义哈希如下： 现在问你长度为n的字符串中，有多少哈希值 % 2 m \%2^m %2m是k 题解： 那么这道题就是个水题， 我一眼就看出来是折半暴力， 2 6 5 26^5 265只有1e7种情况，然后从前往后dfs一下，之后再从后往前，因为它有点特殊，不能像普通哈希一样乘，可以推出来： x ∗ 33 x*33 x∗33^ y = k y=k y=k = > x
Codeforces 1244 C. The Football Season —— 扩展欧几里得
This way 题意： 让你求dx+wy+0z=p,[0<=x,y,z&&x+y+z=n] 题解： 首先很明显可以暴力，因为d和w都是<=1e5的，所以枚举1e5次必然能出答案。 但是我们在学习新知识，所以必然不能这样子去简单地暴力，要搞一点数学的东西进去。 那么很明显是扩展欧几里得，但是裸的板子会有负数的情况，所以我们需要先贪心地放赢得局，因为这样子前两种局数会达到最小，然后剩下的再
Codeforces 7 C. Line —— 扩展欧几里得模板，从零开始の数论
This way 题意： 问你ax+by+c=0的解 题解： 终究还是被迫踏上数论这条道路了，或许以后还会踏上图论的道路… 我其实也大致算个数论小白了，在这个把月能够提升到什么程度也说不好，但是学习进度也可为新手做个参考了。 那么这道题是扩展欧几里得的模板了，求出a和b的gcd之后判断c是否为gcd的倍数，如果是乘上商即可。 #include<bits/stdc++.h>using
数学知识--（欧拉函数，快速幂，扩展欧几里得算法）
本文用于记录个人算法竞赛学习，仅供参考 目录 一.欧拉函数 二.欧拉函数模板 三.用筛法求每个数的欧拉函数 四.快速幂 五.扩展欧几里得算法 六.用扩展欧几里得算法求线性同余方程 一.欧拉函数 即有一个数n， n通过质因数分解得到 通过欧拉函数有 证明：容斥原理 二.欧拉函数模板 实际上就是分解质因数 时间复杂度：O() //
欧几里得算法求解GCD
GCD(最大公约数) 欧几里得算法(辗转相除法) 原理 if(a%b==0)GCD=b elseGCD=b%(a%b) 基本情况： 如果其中一个数为0，则另一个非零数一定就是两数的 G C D GCD GCD(任何非零数与0的GCD都是该非零数本身)。 归纳假设： 假设我们已经证明了对于所有符合条件的 ( a , b ) (a, b) (a,b)，辗转相除法能够正确地给出 g c