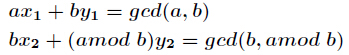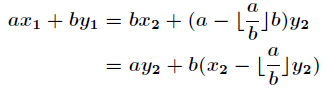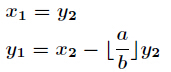poj 2142 拓展欧几里得算法

本文主要是介绍poj 2142 拓展欧几里得算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

扩展欧几里得算法求的是方程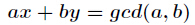的解。原理如下

 

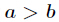
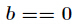
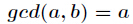
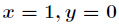
设，当时，，此时，否则设

 

     

 

由于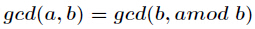，所以进一步得到

 

      

 

所以得到

 

                   

 代码：

void extgcd(int a,int b, int &x, int &y){if(b == 0 && a == 0) return ;if(b == 0){x = 1; y = 0;return ;}extgcd(b, a%b, x, y);int tmp = x;x = y;y = tmp - (a / b) * y;}

题目：poj2142

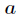
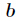
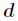
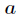
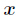
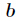
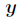
题意：有两种类型的砝码质量分别为和，要求称出质量为的物品，要求的数量和的数量的和

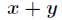
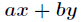
     最小，如果有多个最小值，取最小的。

 

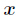
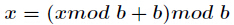
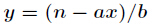
分析：扩展欧几里得求出特解后，把转化为最小正值，即，，若

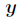
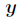
     求出的为负值，则把变正，意思就是砝码放置的位置有左右之分，可以左面的减去右面的，也可以右面

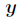
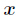
     的减去左面的。同理，再求出为最小合法正值时的解，将这两种情况比较取小的即可。

 

代码：

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int gcd (int a, int b){return b == 0 ? a : gcd(b, a % b);
}
void extgcd(int a,int b, int &x, int &y){if(b == 0 && a == 0) return ;if(b == 0){x = 1; y = 0;return ;}extgcd(b, a%b, x, y);int tmp = x;x = y;y = tmp - (a / b) * y;}
int main(){int a, b, n;while(~scanf("%d%d%d", &a, &b, &n)){if(!a && !b && !n) break;int d = gcd(a, b);a /= d;b /= d;n /= d;int x, y;extgcd(a, b, x, y);int tx = ((x * n) % b + b) % b;int ty = (n - a * tx) / b;if(ty < 0) ty = -ty;y = ((y * n) % a + a) % a;x = (n - b * y) / a;if(x < 0) x = -x;if(x + y > tx + ty){x = tx;y = ty;}printf("%d %d\n", x, y);}return 0;
}

参考：http://blog.csdn.net/acdreamers/article/details/7920027

这篇关于poj 2142 拓展欧几里得算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---