扩展欧几里得算法——AcWing.877扩展欧几里得算法

本文主要是介绍扩展欧几里得算法——AcWing.877扩展欧几里得算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

扩展欧几里得算法

定义

扩展欧几里得算法是用来在已知整数 a、b 的情况下，求解一组整数 x、y 使得 ax + by = gcd(a, b)（gcd 表示最大公约数）。

运用情况

• 求解线性同余方程。
• 在密码学等领域有广泛应用。

注意事项

• 要注意边界情况和特殊值的处理。
• 在计算过程中要注意数据的范围，避免溢出。

解题思路

通过递归的方式不断缩小问题规模。从较大的数对(a, b)逐步递推到较小的数对，直到其中一个数为 0。在递推过程中同时计算出对应的 x 和 y 值。

首先，我们考虑当 a 为 0 时的特殊情况，此时 x 取 0，y 取 1，因为 0 * 0 + b * 1 = b = gcd(0, b)。

然后，对于一般情况，我们通过递归到下一层，即计算 b % a 和 a 的扩展欧几里得解 x1 和 y1。

接下来，通过这一层得到的 x1 和 y1 来推导出当前层的 x 和 y。具体推导公式为 x = y1 - (b / a) * x1，y = x1。

这样不断递归下去，就可以逐步求解出最终满足 ax + by = gcd(a, b) 的 x 和 y。

比如，当计算 gcd(12, 5) 时，先递归到计算 gcd(5, 2)，再到 gcd(2, 1)，最后到 gcd(1, 0) 得到 x = 0，y = 1，然后逐步回推得到 x = -1，y = 2 满足 12 * (-1) + 5 * 2 = 2 = gcd(12, 5)。

在实际应用中，常常用于求解线性同余方程等问题，通过找到这样一组特殊的 x 和 y，可以帮助我们解决很多相关的数学问题。

AcWing.877扩展欧几里得算法

题目描述

877. 扩展欧几里得算法 - AcWing题库

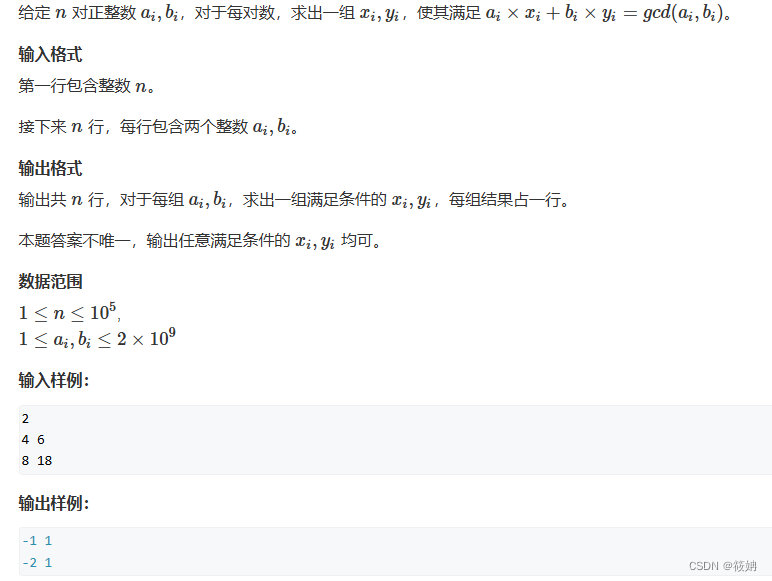
运行代码

#include <iostream>
using namespace std;
void extend(int a, int b, int &x, int &y) {if (a == 0) {x = 0;y = 1;return;}int x1, y1;extend(b % a, a, x1, y1);x = y1 - (b / a) * x1;y = x1;
}
int main() {int n;cin >> n;while (n--) {int a, b;cin >> a >> b;int x, y;extend(a, b, x, y);cout << x << " " << y << endl;}return 0;
}

代码思路

• extend函数是扩展欧几里得算法的实现。
  • 首先处理特殊情况，当a为 0 时，直接设置x为 0，y为 1 并返回，因为此时满足 0x + b1 = b = gcd(0,b)。
  • 对于一般情况，通过递归调用自身来计算b%a和a的扩展欧几里得解x1和y1。
  • 然后根据当前层的参数和递归得到的结果来计算当前层的x和y，即通过公式x = y1 - (b/a)*x1和y = x1来确定。
• 在main函数中：
  • 首先读取对数n。
  • 然后通过循环，对于每一对输入的数a和b，声明变量x和y，调用extend函数来计算满足条件的x和y，并将结果输出到控制台。

其他代码

#include<iostream>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{if(!b){x=1,y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;
}
int main()
{int n;cin>>n;while(n--){int a,b,x,y;cin>>a>>b;exgcd(a,b,x,y);cout<<x<<' '<<y<<endl;}return 0;
}

代码思路

1. 扩展欧几里得算法（exgcd函数）:

   • 函数exgcd(int a, int b, int &x, int &y)接收四个参数，其中a和b是要计算最大公约数的两个整数，x和y是引用类型，用于输出满足 ax + by = gcd(a, b) 的一组整数解。
   • 当b为0时，根据欧几里得算法的基本原理，直接得出a是当前的GCD，此时设置x=1, y=0，因为a1 + 0b = a。
   • 否则，递归调用exgcd(b, a % b, y, x)。这里进行了变量交换，原本的x变为y，原本的y变为x，这是为了正确回溯解的值。
   • 递归调用返回后，根据递归过程中的关系调整y的值，使其满足原始方程 ax + by = gcd(a, b)。具体操作为：y -= a/b*x;。
   • 最终返回计算得到的最大公约数d。

2. 主函数（main）:

   • 首先读取一个整数n，表示接下来有n组数据。
   • 使用一个循环，对于每组数据，读取两个整数a和b。
   • 调用exgcd(a, b, x, y)函数，计算a和b的最大公约数，并找到对应的x和y。
   • 输出x和y的值，每组解之间用空格分隔，每组数据输出后换行。
   • 循环处理完所有数据后，程序结束。

应用场景举例：

• 模逆元计算：在RSA加密算法、中国剩余定理等问题中，需要找到一个整数x，使得 ax ≡ 1 (mod b)，这里可以通过扩展欧几里得算法找到x，当且仅当a和b互质时，x即为a关于模b的乘法逆元。
• 解线性同余方程：求解形式如ax + by = c的方程，尤其是在模意义下的求解，扩展欧几里得算法是基础工具。

这篇关于扩展欧几里得算法——AcWing.877扩展欧几里得算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---