【洛谷P2054洗牌】AC代码(扩展欧几里得+二分快速幂+二分龟速乘)

本文主要是介绍【洛谷P2054洗牌】AC代码(扩展欧几里得+二分快速幂+二分龟速乘)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

题目链接
为了表彰小联为Samuel星球的探险所做出的贡献，小联被邀请参加Samuel星球近距离载人探险活动。

由于Samuel星球相当遥远，科学家们要在飞船中度过相当长的一段时间，小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后，大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。

对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

如果对一叠6张的扑克牌1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

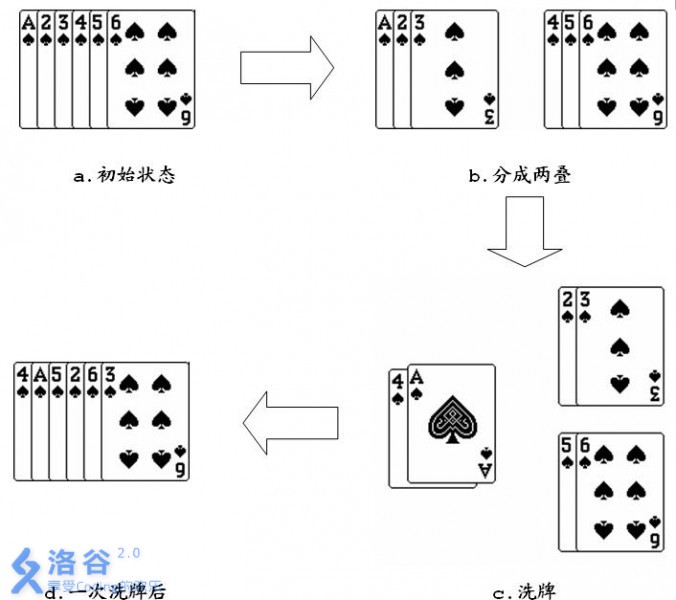
从图中可以看出经过一次洗牌，序列1 2 3 4 5 6变为4 1 5 2 6 3。当然，再对得到的序列进行一次洗牌，又会变为2 4 6 1 3 5。

游戏是这样的，如果给定长度为N的一叠扑克牌，并且牌面大小从1开始连续增加到N（不考虑花色），对这样的一叠扑克牌，进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利，你能帮助他吗？

输入格式

输入文件中有三个用空格间隔的整数，分别表示N，M，L（其中0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数）。

输出格式

单行输出指定的扑克牌的牌面大小。

输入输出样例

• 输入 #1

6 2 3

• 输出 #1

6

• 说明/提示

0＜N≤10^10 ，0≤M≤10^10，且N为偶数

前置知识

扩展欧几里得算法

贝祖定理

• 若有整数a，b，c，在方程$ax+by=c$中，未知数x，y有整数解当且仅当c是gcd(a,b)的倍数，其中gcd(a,b)表示a，b的最大公因数。

欧几里得算法

• gcd(a,b)=gcd(b,a%b)=…=gcd(d,0)=d

算法模板

int gcd(int a,int b){if(b==0) return a;else return gcd(b,a%b);
}

扩展欧几里得算法

• 用于求解$ax+by=gcd(a,b)$。

算法思想
按照欧几里得算法展开方程$ax+by=gcd(a,b)=gcd(b,a\%b)=b{x}^{\prime }+(a\%b)y^{\prime }=...=1d+0y=gcd(a,b)$
其中$b{x}^{\prime }+(a\%b)y^{\prime }=b{x}^{\prime }+(a-a/b\ast b)y^{\prime }=a{y}^{\prime }+(x^{\prime }-a/b\ast y^{\prime })b=ax+by$
即$x=x^{\prime },y=x^{\prime }-a/b\ast y^{\prime }$
最终$gcd(a,b)x_0+0y_0=gcd(a,b)$，即$x_0=1,y_0\in R$，所求得$x,y$只是一组特解，通解为$(x+k\ast b/d,y-k\ast b/d)$，推导方法略

算法模板

typedef long long ll;
ll exgcd(ll a,ll b,ll &x,ll &y){if(b==0){x=1;//gcd(a,b)x=gcd(a,b)y=0;//y随意return a;}ll gcd=exged(b,a%b,x,y),r;r=x;x=y;//x=y'y=r-a/b*y;//y=x'-a/b*y'return gcd;
}

用途

1. 求乘法逆元
2. 求解$ax+by=c$
3. 求同余方程

乘法单位元：任何数乘以单位元等于这个数，显然乘法的单位元是1。
乘法逆元：任何数乘以他的乘法逆元等于单位元，比如2*0.5=1，0.5就是1的乘法逆元，但这不是我们需要的东西，我们需要的是在模运算下的整数乘法逆元。

二分快速幂与二分龟速乘

二分快速幂

二分幂

• 二分幂，就是平常所用的幂运算化简方法，一般采用递归实现，不建议使用

如
$$a^b=\{\begin{array}{l}a\ast {\left(a^2\right)}^{\frac{b}{2}},b\text{为奇数}\\ {\left(a^2\right)}^{\frac{b}{2}},b\text{为偶数}\end{array}$$
转化为递归方程为
$$f\left(a,b\right)=\{\begin{array}{l}1,b=0\\ a\ast f\left(a^2,\frac{b}{2}\right),b\text{为奇数}\\ f\left(a^2,\frac{b}{2}\right),b\text{为偶数}\end{array}$$
算法模板

typedef long long ll;
ll efm(ll a,ll b,ll n){if(b==0) return 1;if(b&1) return a*efm(a*a%n,b>>1,n);else return efm(a*a%n,b>>1,n);
}

快速幂

• 采用二分的思想利用二进制快速求解$a^b$。

算法思想
这里用b表示二进制数，
如$3^{13}=3^{b1101}=3^{1\ast b1000}\ast 3^{1\ast b100}\ast 3^{0\ast b10}\ast 3^{1\ast b1}$
$3^{b10}=(3^{b1}{)}^2$
$3^{b100}=(3^{b10}{)}^2$
$3^{b1000}=(3^{b100}{)}^2$
可以看出，每一项都是前一项的平方，原本需要计算13次的算法被优化到了计算4次，本算法时间复杂度是$O(lo{g}_{2}b)$。

算法模板

• 通常，本算法的幂非常大，所求结果常需要取模

typedef long long ll;
ll ksm(ll a,ll b,ll n){//a^b%nll ret=1;//累乘结果计算while(b>0){//非0次幂则计算if(b&1){//判断最低为是否为1，0不需要乘入ret=ret*a%n;}a=a*a%n;//由上述推导可得平方关系b>>=1;//b右移一位}return ret;
}

二分龟速乘

• 对于快速幂算法的改进

二分快速幂算法存在的问题
在使用二分快速幂计算乘法时，尽管采用了%n来防止溢出，但仍然会有溢出现象，因为x*x%n，在x*x时就有可能溢出。

二分乘

• 其实就是龟速乘的二分版本，一般用递归实现，不建议使用

乘法可以写成累加的形式，诸如
$$3\ast 5=3+3\ast 4=3+(2\ast 3)\ast 2=3+6\ast 2=3+12$$
转化为递归方程为
$$f\left(a,b\right)=\{\begin{array}{l}0,b=0\\ a+f\left(2a,\frac{b}{2}\right),b\text{为奇数}\\ f\left(2a,\frac{b}{2}\right),b\text{为偶数}\end{array}$$
算法模板

typedef long long ll;
ll gsc(ll a,ll b,ll n){if(b==0) return 0;if(b&1) return (a+gsc((a<<1)%n,b>>1))%n;else return gsc((a<<1)%n,b>>1)%n;
}

龟速乘

我们可以让x*y也变成类似于快速幂的运算形式，诸如
$3\ast 5=3\ast b101=3\ast (1\ast b1+0\ast b10+1\ast b100)$
$=1\ast 3\ast b1+0\ast 3\ast b10+1\ast 3\ast b100$
其中
$3\ast b10=3\ast b1+3\ast b1$
$3\ast b100=3\ast b10+3\ast b10$
不难发现，每一项都是前一项的二倍，由于本算法甚至慢于for循环相加，故得名龟速乘，时间复杂度为$O(lo{g}_{2}b)$

算法模板

typedef long long ll;
ll gsc(ll a,ll b,ll n){ll ret=0;//累加结果计算while(b>0){//非0乘则计算if(b&1){//判断最低为是否为1，0不需要加入ret=(ret+a)%n;}a=(a+a)%n;//由上述推导可得平方关系b>>=1;//b右移一位}return ret;
}

快速幂的改进

• 引入了龟速乘后，我们便可以改进快速幂算法

typedef long long ll;
ll ksm(ll a,ll b,ll n){ll ret=1;while(b>0){if(b&1){ret=gsc(ret,a,n);//修改位}a=gsc(a,a,n);//修改位b>>=1;}return ret;
}

题解

根据题目不难看出在$n$张牌中第$x$张牌经过$m$伦洗牌后与所在位置$l$满足：
$$x\ast 2^m=l(modn+1)$$
两种解法:

1. 通过同余方程求逆元解答
2. 直接求同余方程解

由于本文旨在学习更多的知识，采用逆元解法
这是线性同余方程，需要快速幂结合扩展欧几里得算法求解。
由于$ax=b(modn)$，令$d=gcd(a,n),t=n/d$，则$x$的最小正整数解为$x=(x\%t+t)\%t$，在本题中$a$为偶数，$n+1$为奇数，则$t=n$

快速幂+龟速乘代码

#include <iostream>
using namespace std;
typedef long long ll;
ll n,m,l,x,y;
ll gsc(ll x,ll m){ll ret=0;while(m){if(m&1) ret=(ret+x)%n;x=(x+x)%n;m>>=1;}return ret;
}
ll ksm(ll x,ll m){ll ret=1;while(m){if(m&1) ret=gsc(ret,x);x=gsc(x,x);m>>=1;}return ret;
}
ll exgcd(ll a,ll b,ll &x,ll &y){if(b==0){x=1;y=0;return a;}ll r=exgcd(b,a%b,x,y);ll c=x;x=y;y=c-a/b*y;return r;
}
int main(){scanf("%lld%lld%lld",&n,&m,&l);n++;ll k=ksm(2,m);exgcd(k,n,x,y);x=gsc(l,x%n+n);printf("%lld",x%n);return 0;
}

二分幂+二分乘代码

#include <iostream>
using namespace std;
typedef long long ll;
ll n,m,l,x,y;
ll efc(ll x,ll m){if(m==0) return 0;if(m&1) return (x+efc((x<<1)%n,m>>1))%n;else return efc((x<<1)%n,m>>1)%n;
}
ll efm(ll x,ll m){if(m==0) return 1;if(m&1) return efc(x,efm(efc(x,x)%n,m>>1));else return efm(efc(x,x)%n,m>>1);
}
ll exgcd(ll a,ll b,ll &x,ll &y){if(b==0){x=1;y=0;return a;}ll r=exgcd(b,a%b,x,y);ll c=x;x=y;y=c-a/b*y;return r;
}
int main(){scanf("%lld%lld%lld",&n,&m,&l);n++;ll k=efm(2,m);exgcd(k,n,x,y);x=efc(l,x%n+n);printf("%lld",x%n);return 0;
}

扩展

快速乘

• 经Cyan_rose介绍，《论程序底层优化的一些方法与技巧》这篇论文中提到了快速乘

• 可以按此代码实现快速乘

cin>>a>>b>>mod;
cout<<((a*b-(long long)((long double)a*b/mod)*mod+mod)%mod);

这篇关于【洛谷P2054洗牌】AC代码(扩展欧几里得+二分快速幂+二分龟速乘)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---