.norm() 范数

2024-02-27 00:12

文章标签 norm 范数

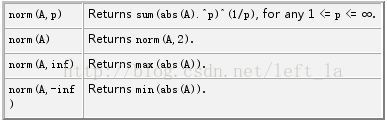
本文主要是介绍.norm() 范数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

(A- B).norm().item()

是默认计算A与B的第二范数，如果你想计算差向量的第一范数（也称为L1范数），可以在norm()方法中传递p=1参数，这样就会计算出L1范数。例如：

(A- B).norm(p=1).item()

其中，使用.item()方法将结果转换为Python的标量（scalar）类型

这篇关于.norm() 范数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/750618。 23002807@qq.com

Pytorch中不同的Norm归一化详细讲解

在做项目或者看论文时，总是能看到Norm这个关键的Layer，但是不同的Norm Layer具有不同的作用，准备好接招了吗？（本文结论全部根据pytorch官方文档得出，请放心食用）一. LayerNorm LayerNorm的公示如下： y = x − E [ x ] Var ⁡ [ x ] + ϵ ∗ γ + β y=\frac{x-\mathrm{E}[x]}{\sqrt{\op

CV-CNN-2015：GoogleNet-V2【首次提出Batch Norm方法：每次先对input数据进行归一化，再送入下层神经网络输入层（解决了协方差偏移问题）】【小的卷积核代替掉大的卷积核】

GoogLeNet凭借其优秀的表现，得到了很多研究人员的学习和使用，因此GoogLeNet团队又对其进行了进一步地发掘改进，产生了升级版本的GoogLeNet。 GoogLeNet设计的初衷就是要又准又快，而如果只是单纯的堆叠网络虽然可以提高准确率，但是会导致计算效率有明显的下降，所以如何在不增加过多计算量的同时提高网络的表达能力就成为了一个问题。 Inception V2版本的解决方案就是修

python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)（向量的第二范数为传统意义上的向量长度），（如何求取向量的单位向量）

转载自： https://www.cnblogs.com/devilmaycry812839668/p/9352814.html 求取向量二范数，并求取单位向量（行向量计算） import numpy as npx=np.array([[0, 3, 4], [2, 6, 4]])y=np.linalg.norm(x, axis=1, keepdims=True)z=x/y x 为需

关于范数的介绍

作者：Faaany 链接：https://www.zhihu.com/question/21868680/answer/136376374 来源：知乎著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。要更好的理解范数，就要从函数、几何与矩阵的角度去理解，我尽量讲的通俗一些。我们都知道，函数与几何图形往往是有对应的关系，这个很好想象，特别是在三维以下的空间内，函数是几

概率统计Python计算：连续型随机变量分布（norm）

scipy.stats的norm对象表示正态分布，下表说明norm的几个常用函数。函数名参数功能rvs(loc, scale, size)loc，scale：分布参数 μ \mu μ和 σ \sigma σ，缺省值分别为0和1，size：产生的随机数个数，缺省值为1产生size个随机数pdf(x, loc, scale)x：自变量取值，loc，scale：与上同概率密度函数 f ( x )

【转】常见向量范数和矩阵范数

1、向量范数 1-范数：，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。 2-范数：，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。 ∞-范数：，即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。 -∞-范数：，即所有向量元素绝对值中的最小值，matlab调用函数nor

$l0-Norm, l1-Norm, l2-Norm, … , l-infinity Norm$