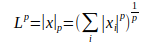本文主要是介绍关于向量的模和向量的范数的理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
向量的模
含义
向量 
的长度叫做向量的模，记作 
，也就是向量 的大小
计算公式
对于向量 
属于n维复向量空间
=(x1,x2,…,xn)
的模为 
= 
向量的范数
范数，在机器学习中通常用于衡量一个向量的大小，形式上， 范数的定义如下：
其中 p>=1
比如如下常见的范数
1-范数：║x║1=│x1│+│x2│+…+│xn│ （曼哈顿距离）
2-范数：║x║2=（│x1│2+│x2│2+…+│xn│2）1/2 （欧式距离）
∞-范数：║x║∞=max（│x1│，│x2│，…，│xn│） （切比雪夫距离）
大家可以发现，向量的模和向量的L2范数的计算方式都是一样的，都表示的是欧氏距离。
可以简单理解，范数是表示向量的大小，但是不同的空间，不同的应用场景可以选择不同的衡量方式，
但是向量的模是固定的，就是指欧氏距离。
因此向量的模 ==向量的L2范数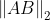
这篇关于关于向量的模和向量的范数的理解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
