聚类分析专题

MATLAB层次聚类分析法

转自：http://blog.163.com/lxg_1123@126/blog/static/74841406201022774051963/ 层次聚类是基于距离的聚类方法，MATLAB中通过pdist、linkage、dendrogram、cluster等函数来完成。层次聚类的过程可以分这么几步： (1) 确定对象（实际上就是数据集中的每个数据点）之间的相似性，实际上就是定义一个表征

数学建模--K-Means聚类分析

目录 1.聚类分析步骤 1.1简单介绍 1.2两个概念 1.3几种距离 1.4更新质心 1.5终止条件 2.归一化处理 3.肘部法则 4.搭建K-Means分析模型 5.选择最佳K值 6.绘制3D图形 1.聚类分析步骤 1.1简单介绍 K-Means聚类分析是属于聚类分析的一种，这个数据机器学习的算法；对数据进行自动分组，使得同一组内的数据样本尽可能相似

基于数据挖掘的消费者商品交易数据分析可视化与聚类分析

文章目录 ==有需要本项目的代码或文档以及全部资源，或者部署调试可以私信博主==项目介绍项目实现实现流程实现过程数据预处理EDA探索性数据分析聚类分析每文一语有需要本项目的代码或文档以及全部资源，或者部署调试可以私信博主项目介绍基于python的消费者商品交易数据分析与可视化主要包含以下内容: 首先探讨如何从各种渠道获取消费者商品交易数据，例如电子商务网站的API、

综合评价 | 基于因子分析和聚类分析的节点重要度综合评价（Matlab）

目录效果一览基本介绍程序设计参考资料效果一览基本介绍综合评价 | 基于因子分析和聚类分析的节点重要度综合评价（Matlab）程序设计完整程序和数据获取方式：私信博主回复基于因子分析和聚类分析的节点重要度综合评价（Matlab）。参考资料 [1] http://t.csdn.cn/pCWSp [2] https://download.

聚类分析 #数据挖掘 #Python

聚类分析（Cluster Analysis）是一种无监督机器学习方法，主要用于数据挖掘和数据分析中，它的目标是将一组对象或观测值根据它们之间的相似性或相关性自动分组，形成不同的簇或类别。聚类分析并不预先知道每个观测值的具体标签，而是基于数据本身的内在结构进行分组。聚类过程主要包括以下几个步骤：选择算法：常见的聚类算法有K-means、层次聚类（如凝聚层次聚类和分裂层次聚类）、DBSCAN、

聚类分析模板

聚类分析主要包括样本相似性度量，类与类间相似性度量两个步骤。（1）样本的相似性度量在对样本进在行聚类分析时，首先要确定样本的相似性度量，常用的样本相似性度量有马氏距离、车比雪夫距离、欧式距离等，下面介绍最常用的欧式距离法。记是样本点集，距离是的一个函数，满足条件： ① ② ③ ④ 这一距离的定义满足正定性、对称性和三角不等式。在聚类分析中，对于定量变量，最常用

python数据分析-房价数据集聚类分析

一、研究背景和意义随着房地产市场的快速发展，房价数据成为了人们关注的焦点。了解房价的分布特征、影响因素以及不同区域之间的差异对于购房者、房地产开发商、政府部门等都具有重要的意义。通过对房价数据的聚类分析，可以深入了解房价的内在结构和规律，为相关决策提供科学依据。研究意义：为购房者提供参考：通过聚类分析，可以将房价数据分为不同的类别，购房者可以根据自己的需求和预算选择适合的房源。帮助房地

KMeans聚类分析星

1. datasample initial_centroids = datasample(data, k, 'Replace', false); 是MATLAB中的命令，用于从数据集data中随机抽取k个样本作为初始聚类汇总新，并且抽取时不放回。 datasample：是MATLAB中的函数，用于从数组中随机抽取样本data：是你想要进行聚类分析的数据集，通常是包含了所有待分类样本特征

数据挖掘--聚类分析：基本概念和方法

数据挖掘--引论数据挖掘--认识数据数据挖掘--数据预处理数据挖掘--数据仓库与联机分析处理数据挖掘--挖掘频繁模式、关联和相关性：基本概念和方法数据挖掘--分类数据挖掘--聚类分析：基本概念和方法聚类分析聚类分析是把一个数据对象（或观测）划分成子集的过程每一个对象都是一个簇划分方法 k－均值 k－中心点基于密度的方法

数学建模 —— 聚类分析（3）

目录一、聚类分析概述 1.1 常用聚类要素的数据处理 1.1.1 总和标准化 1.1.2 标准差标准化 1.1.3 极大值标准化 1.1.4 极差的标准化 1.2 分类 1.2.1 快速聚类法（K-均值聚类） 1.2.2 系统聚类法（分层聚类法）二、分类统计量距离 2.1 明式（Minkowski）距离 2.2 马氏（Mahalanobis）距离 2.3 兰氏（C

基于鸢尾花数据集实施自组织神经网络聚类分析

基于鸢尾花数据集实施自组织神经网络聚类分析 1. 自组织神经网络的基础知识2. 鸢尾花数据集的自组织分类3. SOM的无监督聚类 1. 自组织神经网络的基础知识自组织神经网络也称自组织映射（SOM）或自组织特征映射（SOFM），是一种使用非监督式学习来产生训练样本的输入空间的一个低维（通常是二维）离散化的表示的人工神经网络（ANN）。自组织映射与其他人工神经网络的不同之处在于它

SPSS之聚类分析

SPSS中系统聚类分析功能在【分析】—【分类】—【系统聚类】中完成。系统聚类有两种类型，一种是对样本进行聚类，称为Q型聚类；一种是对变量进行聚类，称为R型聚类。在【系统聚类分析】—【聚类】框下选择【个案】——Q型聚类，或是【变量】——R型聚类。如果参与聚类分析的变量存在数量级上的差异，应在SPSS中，通过【系统聚类分析】—方法(M)—【系统聚类分析：方法】—【转换值】—【标准化】选项中选择消除

SAS 聚类分析—— K-均值聚类

K-均值方法，有时也叫劳埃德方法或 Lioyd-Forgy 方法。 K-均值聚类的核心思想是为指定划分数目的最佳划分。对于 n 个观测，每个观测是 m 维的实数向量，现在需要找到 k 个聚类（其中 k <= n,即 n 个子集），使得每个类别分组内的方差最小化。 K-均值聚类的基本步骤如下： 1.随机选取 k 个真实/或虚拟的数据点作为初始质心（即选择 k 个样品作为初始凝聚点，或者将

探索数据之美：简述多元统计分析中的聚类分析

在现代科学研究和商业决策中，我们常常面对着海量的数据。如何从这些数据中提取有用的信息？这就是统计学的任务之一。而聚类分析作为多元统计分析中的一种技术，能够帮助我们在数据中发现隐藏的模式和结构。本文将带您一起探索聚类分析的奥秘，了解它是如何工作的以及在实际生活中的应用。什么是聚类分析？聚类分析是一种无监督学习的方法，其主要目的是将一组数据点划分为具有相似特征的若干个组（或者称为簇）。换句话说

《R语言与农业数据统计分析及建模》学习——聚类分析

聚类分析时一种分类技术。与回归分析、判别分析被一起成为多元分析的三大方法。根据分类的方法可将聚类分析分为：层次聚类、快速聚类等。 1、层次聚类（1）定义每个观测值（行或单元）为一类（2）计算每类和其他各类的距离（3）把距离最短的两类合并成一类，这样类的个数就减少一个（4）重复步骤（2）（3），知道包含

聚类分析字符串数组

聚类分析字符串数组对多个字符串进行聚类分析旨在根据它们之间的相似度将这些字符串划分成若干个类别，使得同一类别内的字符串彼此相似度高，而不同类别间的字符串相似度低小结数据要清洗。清洗的足够准确，可能不需要用聚类分析了数据要多，聚集点要少，点阵就集中步骤 1: 数据预处理标准化：统一字符串的大小写、去除无关字符（如标点符号、空格等）。步骤 2: 特征提取词频统计：对于每个

【python机器学习】python电商数据K-Means聚类分析可视化（源码+数据集+报告）【独一无二】

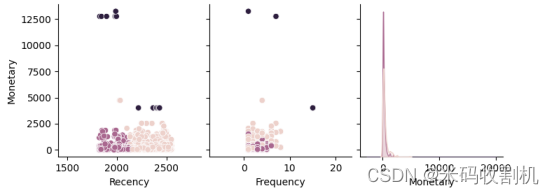
👉博__主👈：米码收割机 👉技__能👈：C++/Python语言 👉公众号👈：测试开发自动化【获取源码+商业合作】 👉荣__誉👈：阿里云博客专家博主、51CTO技术博主 👉专__注👈：专注主流机器人、人工智能等相关领域的开发、测试技术。系列文章目录目录系列文章目录一、设计目的1.1 论文展示二、聚类分析及数据可视化2.1. 数据总览2.2. 买家

机器学习_逻辑回归、聚类分析、模型调用与保存

一、模型的加载与保存 # 保存训练好的模型joblib.dump(自己命名分类器名称, "保存地址")# 比如 lr = LogisticRegression(),那里就写lr# 调用保存好的模型(训练好的)去做预测model = joblib.load("地址")y_predict = model.predict(x_test)# 当我们的x,y都被正则化的时候#y_predict

聚类分析 | 聚类有效性评价指标外部NMI（MATLAB）

指标解释聚类有效性评价指标中的外部NMI（Normalized Mutual Information，归一化互信息）是一种常见的外部有效性指标，用于评估聚类结果与真实标签之间的相似度。NMI从信息论的角度出发，衡量两个聚类结果的共享信息量。 NMI的计算基于聚类结果和真实标签之间的互信息以及各自的熵。互信息表示两个随机变量之间的共享信息，而熵则衡量随机变量的不确定性。NMI的取值范围为[0,

使用DTW算法对上证50成分股走势进行聚类分析

0.背景客户要求对发电机组的过程参数进行分析，把走势异常的工艺过程数据挑出来。研究这个需求的时候感觉可能DTW算法比较合适。关于DTW算法的描述前人描述很多。知乎中这位大神的收藏夹有很多关于时间序列算法的描述。时间序列相似度以及聚类 - 收藏夹 - 知乎想着搞点数据来试试才知道效果怎么样以及学会怎么用。然而甲方的数据倒腾起来太费劲。最好搞的数据是从富途上扒拉股票数据。于是决定把

打造城市二手房分析与可视化系统+聚类分析+58爬虫+线性回归

打造城市二手房分析与可视化系统+聚类分析+58爬虫+线性回归利用数据实现全面分析数据分析与可视化功能创新的聚类分析功能结语在如今房地产市场日益复杂的背景下，对于投资者、购房者和市场分析师来说，了解市场动态并做出明智的决策至关重要。基于此，我们开发了一款基于Python的城市二手房分析与可视化系统，为用户提供了强大的工具，帮助他们深入了解当地房地产市场。利用数据实现全面

使用R语言进行聚类分析

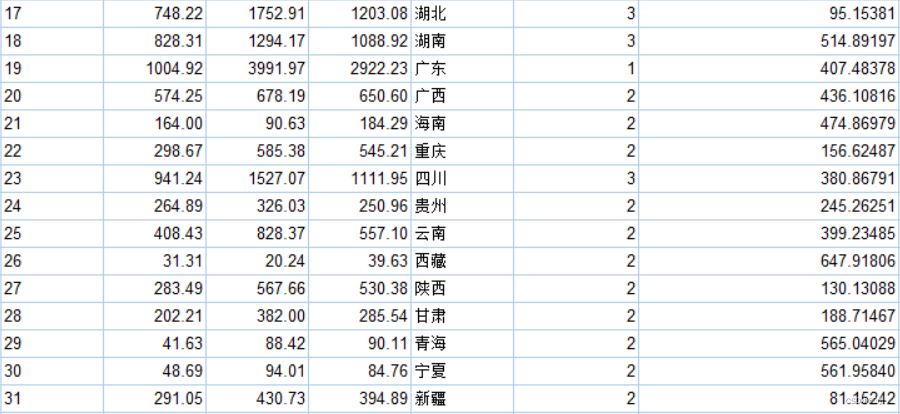
一、样本数据描述城镇居民人均消费支出水平包括食品、衣着、居住、生活用品及服务、通信、文教娱乐、医疗保健和其他用品及服务支出这八项指标来描述。表中列出了2016年我国分地区的城镇居民的人均消费支出的原始数据，数据来源于2017年的《中国统计年鉴》，现要求对下面的数据进行聚类分析。 x1:食品烟酒支出，x2:衣着支出，x3:居住支出，x4:生活用品和服务支出， x5:交通通信支出，x6:教育文

聚类分析|基于层次的聚类方法及其Python实现

聚类分析|基于层次的聚类方法及其Python实现 0. 基于层次的聚类方法1. 簇间距离度量方法1.1 最小距离1.2 最大距离1.3 平均距离1.4 中心法1.5 离差平方和 2. 基于层次的聚类算法2.1 凝聚（Agglomerative）2.3 分裂（Divisive） 3. 基于层次聚类算法的Python实现 0. 基于层次的聚类方法层次聚类（Hierarchical

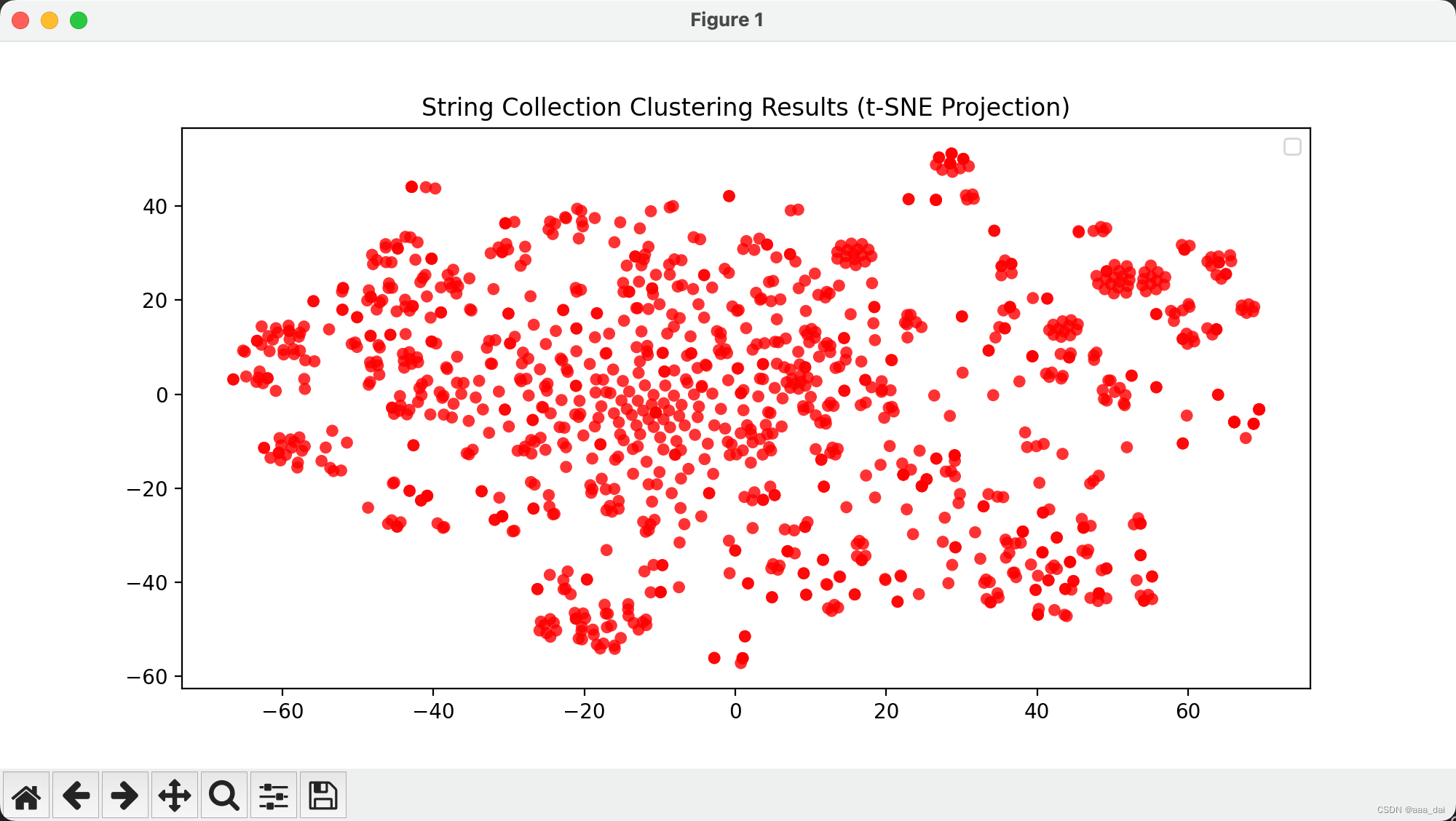
Python文本聚类分析实例（24.03.13更新）

一、引言一个小小学术比赛交叉赛道的技术佐料，目的是给队友爬下来的某音平台下的三农博主进行分类，思路是根据爬取的每个博主的10个标题，先合并成无空格的标题合并文本，然后对这段文本进行预处理（停用词等）、分词，计算文本相似度，最后进行聚类。整体文章的很多代码和思路借鉴了深度学习与文本聚类：一篇全面的介绍与实践指南-CSDN博客，但是没有用到里面的深度学习模型训练，仅仅是对文本进行了聚类。关于更

聚类分析 | Matlab实现基于NNMF+DBO+K-Medoids的数据聚类可视化

聚类分析 | Matlab实现基于NNMF+DBO+K-Medoids的数据聚类可视化目录聚类分析 | Matlab实现基于NNMF+DBO+K-Medoids的数据聚类可视化效果一览基本介绍程序设计参考资料效果一览基本介绍 NNMF+DBO+K-Medoids聚类，蜣螂优化算法DBO优化K-Medoids 非负矩阵分解（NNMF）、蜣螂优化算法（DBO）、以

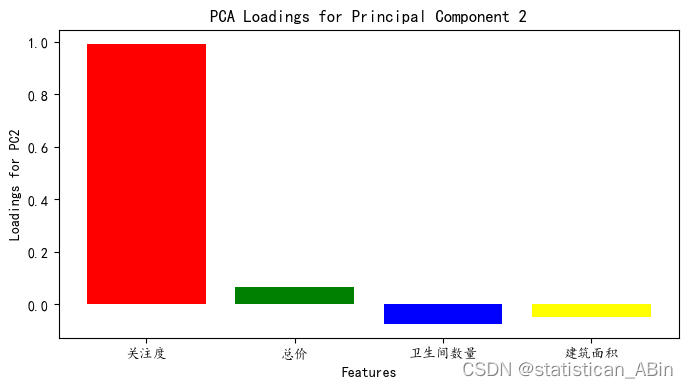
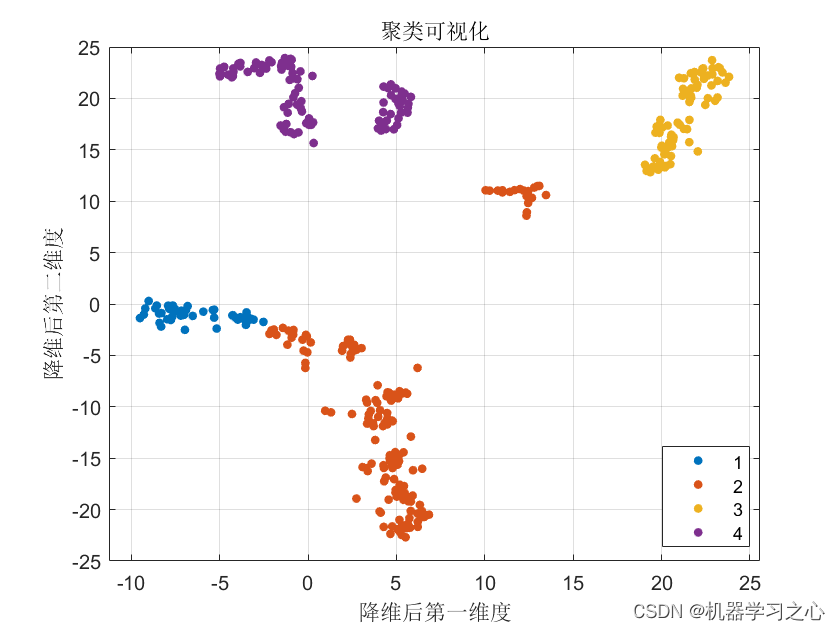
聚类分析 | Matlab实现基于PCA+DBO+K-means的数据聚类可视化

聚类分析 | Matlab实现基于PCA+DBO+K-means的数据聚类可视化目录聚类分析 | Matlab实现基于PCA+DBO+K-means的数据聚类可视化效果一览基本介绍程序设计参考资料效果一览基本介绍 PCA（主成分分析）、DBO（蜣螂优化算法）和K-means聚类是三种不同的数据处理和优化的方法，它们可以结合起来使用以改进聚类效果。下面是对这三种