本文主要是介绍数学建模 —— 聚类分析(3),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、聚类分析概述
1.1 常用聚类要素的数据处理
1.1.1 总和标准化
1.1.2 标准差标准化
1.1.3 极大值标准化
1.1.4 极差的标准化
1.2 分类
1.2.1 快速聚类法(K-均值聚类)
1.2.2 系统聚类法(分层聚类法)
二、分类统计量距离
2.1 明式(Minkowski)距离
2.2 马氏(Mahalanobis)距离
2.3 兰氏(Canberra)距离
三、常用的聚类方法
3.1 最短距离法
3.2 最长距离法
3.3 中间距离法
3.4 重心法
3.5 类平均法
3.6 离差平方和法
四、Matlab进行聚类
五、SPSS步骤
一、聚类分析概述
聚类分析根据一批样品的许多观测指标,按照一定的数学公式具体地计算一些样品或一些参数(指标)的相似程度,把相似的样品或指标归为一类,把不相似的归为一类。
在聚类分析中,聚类要素的选择是十分重要的,它直接影响分类结果的准确性和可靠性。而为了使不同量纲,不同取值范围的数据能够放在一起进行比较,在进行聚类分析之前,首先要对聚类要素进行数据处理。
1.1 常用聚类要素的数据处理
1.1.1 总和标准化
分别求出各聚类要素所对应的数据的总和,以各要素的数据除以该要素的数据的总和,即
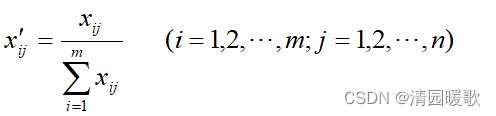
这种标准化方法所得到的新数据满足
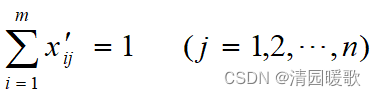
1.1.2 标准差标准化
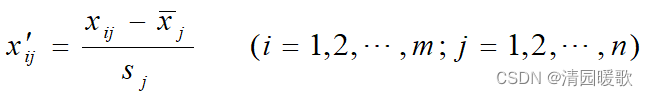
由这种标准化方法所得到的新数据,各要素的平均值为0,标准差为1,即有
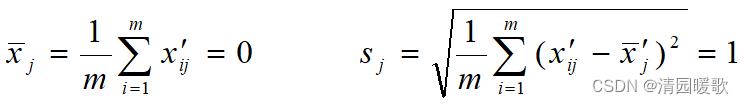
1.1.3 极大值标准化
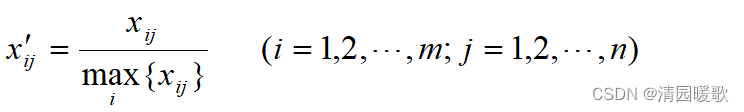
经过这种标准化所得的新数据,各要素的极大值为1,其余各数值小于1。
1.1.4 极差的标准化
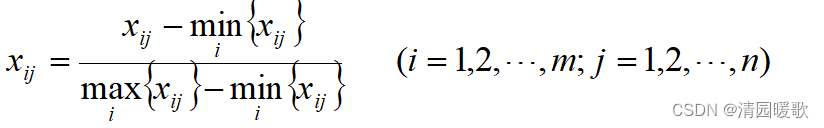
经过这种标准化所得的新数据,各要素的极大值为1,极小值为0,其余的数值均在0与1之间。
1.2 分类
1.2.1 快速聚类法(K-均值聚类)
基本思想:开始时按照一定方法选取一批凝聚点,然后让样本向最近的凝聚点聚类,形成初始分类,之后再按照最近距离原则修改不合理的分类,直到合理为止。
快速聚类过程是寻找初始分类的有效方法,采用的算法是最小化与类均值间距离平方和的标准迭代算法,其结果是高效率地生成大数据文件的不相交的分类

1.2.2 系统聚类法(分层聚类法)
系统聚类的一般程序:
首先,不论是定量数据还是定性数据,都应确定分类统计量,用以测定样本之间的亲疏程度,主要通过样本之间的距离、样本间的相关系数来确定;
分类统计量:样本间的距离或相关系数。
其次,利用统计量将样品进行分类。
二、分类统计量距离



2.1 明式(Minkowski)距离
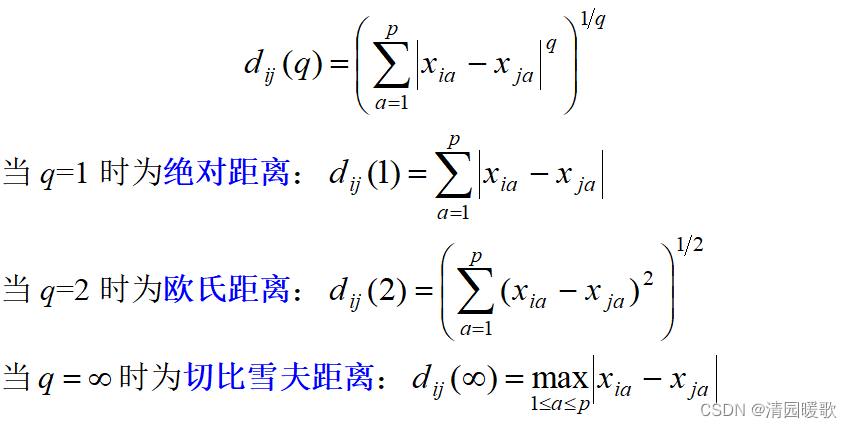

2.2 马氏(Mahalanobis)距离



2.3 兰氏(Canberra)距离

2.相关系数

三、常用的聚类方法
八种聚类计算距离的递推公式:最短距离法、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法、离差平方和法
3.1 最短距离法


步骤:
3.2 最长距离法


3.3 中间距离法

3.4 重心法


3.5 类平均法

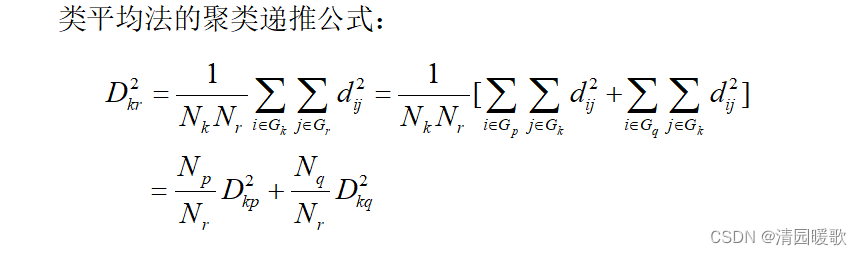
3.6 离差平方和法

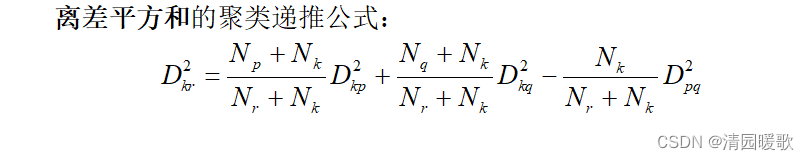
四、Matlab进行聚类





五、SPSS步骤

这篇关于数学建模 —— 聚类分析(3)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!










