本文主要是介绍SPSS之聚类分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
SPSS中系统聚类分析功能在【分析】—【分类】—【系统聚类】中完成。系统聚类有两种类型,一种是对样本进行聚类,称为Q型聚类;一种是对变量进行聚类,称为R型聚类。在【系统聚类分析】—【聚类】框下选择【个案】——Q型聚类,或是【变量】——R型聚类。
如果参与聚类分析的变量存在数量级上的差异,应在SPSS中,通过【系统聚类分析】—方法(M)—【系统聚类分析:方法】—【转换值】—【标准化】选项中选择消除数量级差的方法。并指定处理是针对变量还是针对样本的。
SPSS中提供多种系统聚类方法,常用的是组间平均链接和组内平均链接。通过【系统聚类分析】—方法(M)—【系统聚类分析:方法】—【聚类方法】选项中选择。SPSS提供多种个体距离的计算方式,常用的是Euclidean距离,平方Euclidean距离,Pearson相关性。通过【系统聚类分析】—方法(M)—【系统聚类分析:方法】—【测量】—【区间】选项中选择。
分类数的确定。
(1)系统聚类中每次合并的类与类之间的距离可以作为确定类数的一个辅助工具。首先把离得近的类合并,在并类过程中聚合系数呈增加趋势,聚合系数小,表示合并的两类的相似程度较大,两个差异很大的类合到一起,会使该系数很大。
如果以y轴为聚合系数,x轴表示分类数(n-1,n-2,…,3,2,1),画出聚合系数随分类数的变化曲线,会得到类似于因子分析中的碎石图,可以在曲线开始变得平缓的点选择合适的分类数。SPSS中通过【图形】—【旧对话框】—【散点/点状】实现。
(2)从实用的角度出发,选择合适的分类数。
如果确定分类数,可一开始就在SPSS中指定类数。通过【系统聚类分析】—统计量(S)—【系统聚类分析:统计】—【聚类成员】选项中选择【单一方案】—输入方案数目,或选择【方案范围】。在【系统聚类分析】—保存(A)—【系统聚类分析:保存】—【聚类成员】选项下作同样选择。此时聚类分析的结果将以变量名为clun_m(如clu2_1)的新变量存入SPSS数据编辑窗口中。
SPSS中快速聚类法(K-均值聚类法)在【分析】--【分类】--【K-平均值聚类】中完成。首先应指定聚类数目K,在【K-平均值聚类分析】—【聚类数】框中输入聚类数目,该数应小于样本数。然后SPSS确定k个类的初始类中心点。SPSS会根据样本数据的实际情况,选择k个有代表性的样本数据作为初始类中心。初始类中心也可以由用户自行指定,需要指定K组样本数据作为初始类中心点。
最优方案原则。一般我们希望得到的聚类大小大致相等,这样把每个样品都分配到离它最近的聚类中心(即均值点)就是比较正确的分配方案。
聚类的目的是使类间差异尽量大,而类内差异尽量小,K-均值聚类分析中的方差分析提供这种检验功能。SPSS中通过在【K-平均值聚类分析】— 选项(O) —【统计量】选项中勾选【ANOVA表】来完成方差分析。
SPSS中通过在【K-平均值聚类分析】— 保存(S) 菜单下,勾选【聚类成员】,则聚类分析的结果将以变量名为QCL_m(如QCL_1)的新变量存入SPSS数据编辑窗口中。
接下来我们进行SPSS实战训练!
地区三大产业产值.sav,给出了31个省、直辖市、自治区的三大产业的生产产值数据,即样品数n=31,变量数p=3。对这31个地区的三大产业发展水平进行系统聚类分析,其中个体距离采用平方欧式距离,类间距离采用平均组间链接距离。
(1)系统聚类分析实现步骤:
未确定类数前:[Analyze]→[Classify]→[Hierarchical Cluster Analysis]对话框。将‘第一产业’、‘第二产业’、‘第三产业’添加进Variables中,将‘Region’添加进Label Cases by中。
- 1.在[Statistics]对话框中选择‘Range of solutions’,并将Minimum number of clusters输入‘4’,Maximum number of clusters输入‘5’;
- 2.在[Plots]对话框中勾选中‘Dendrogram’;
- 3.在[Method]对话框中选择‘Between-groups linkage’的Cluster Method;
- 4.在[Save]对话框中的‘Range of solutions’,并将Minimum number of clusters输入‘4’,Maximum number of clusters输入‘5’,将输出结果保存到数据集中。
- 系统聚类分析结果分析:
系统聚类分析凝聚状态表:
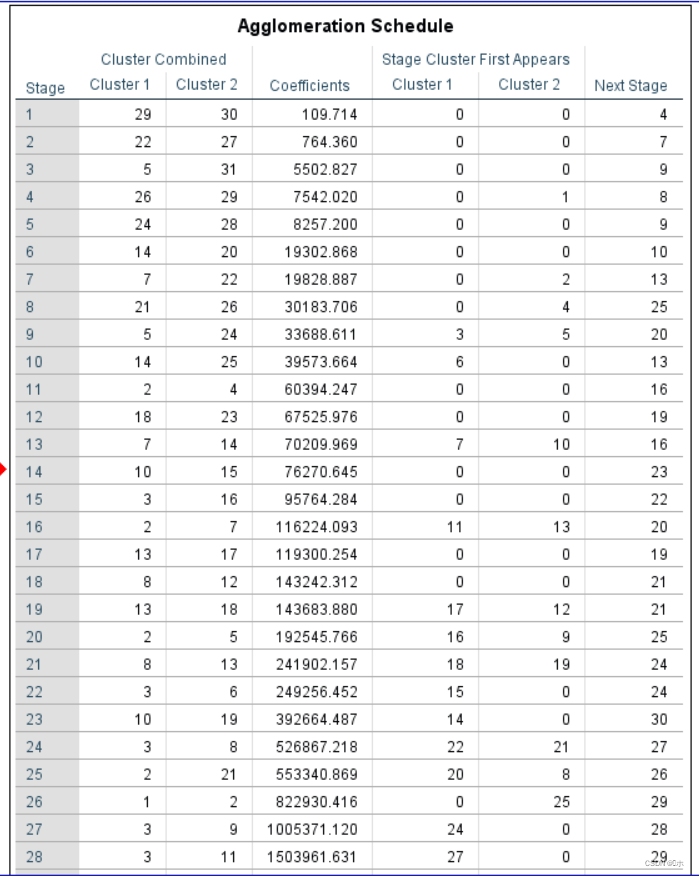

A.个体距离(指 平方欧式距离 )
B.个体与小类的距离(指 组内平局链锁距离 )
C.小类与小类的距离(指 组间平均链锁距离 )
- 第1步: 29 样本和 30 样本聚成一小类,它们的个体距离(欧式距离的平方)是 109.714 ,这个小类将在下面第 4 步用到。
- 第7步: 7样本 和 22样本 聚成一小类,它们的距离是 19828.887,形成的小类将在下面第13步中用到。
- 第9步:5 样本和 24 样本聚成一小类,它们的个体距离(欧式距离的平方)是 33688.611 ,这个小类将在下面第 20 步用到。
冰柱图:
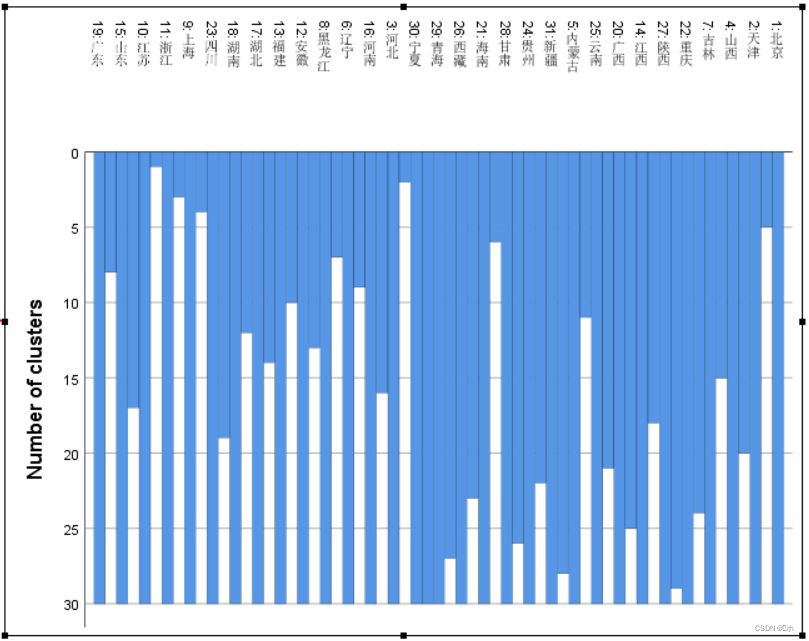
如果分为五类,分类情况是:
第一类为:北京、天津、山西、内蒙古、吉林、江西、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆
第二类为:河北、辽宁、黑龙江、安徽、福建、河南、湖北、湖南、四川
第三类为:上海
第四类为:江苏、山东、广东
第五类为:浙江
树状图:
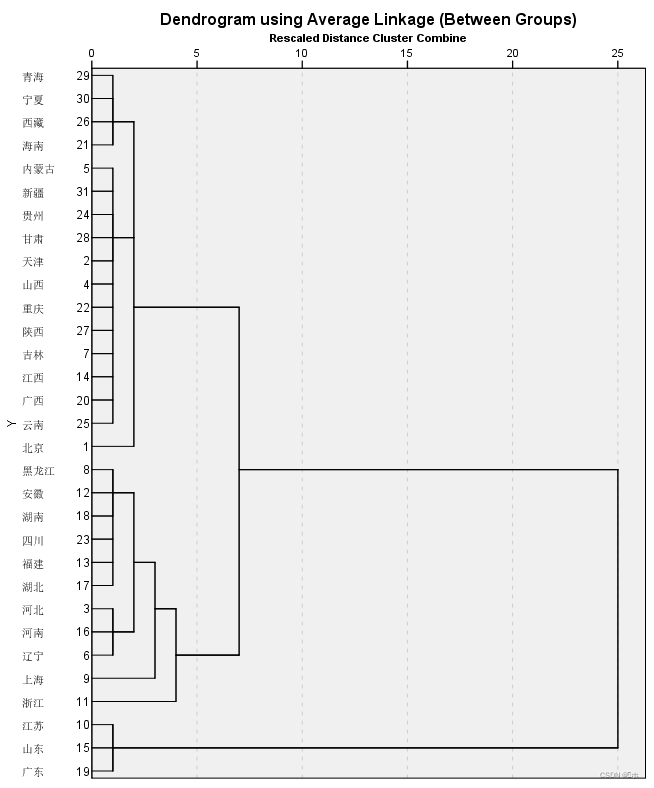
结论:如果分为四类,分类情况是:
- 第一类为: 北京、天津、山西、内蒙古、吉林、江西、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆;
- 第二类为:河北、辽宁、黑龙江、上海、安徽、福建、河南、湖北、湖南、四川;
- 第三类为:江苏、山东、广东;
- 第四类为:浙江;
聚合系数(y轴)与分类数(x轴)的碎石图:
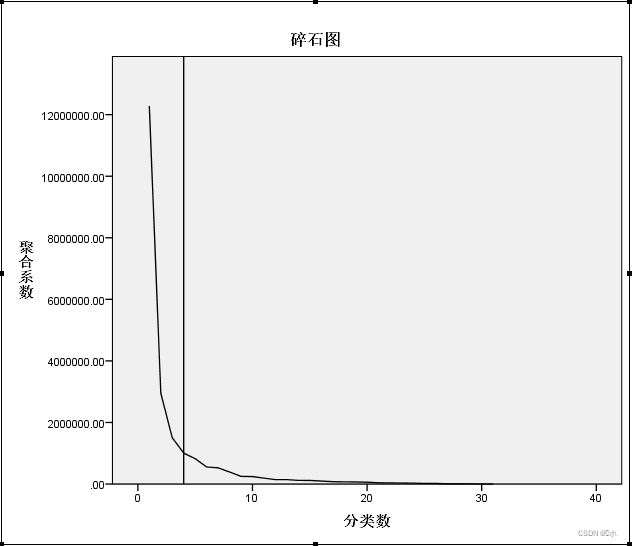
结论:第4 类以后,变化的趋势开始趋于平稳,所以,考虑分为 4 类。
确定类数后:(将聚类结果确定为4类)
[Analyze]→[Classify]→[Hierarchical Cluster Analysis]对话框。将‘第一产业’、‘第二产业’、‘第三产业’添加进Variables中,将‘Region’添加进Label Cases by中。
- 1.在[Statistics]对话框中选择‘Single of solutions’,并输入‘4’;
- 2.在[Save]对话框中的‘Single of solutions’,并输入‘4’,将输出结果保存到数据集中。
分类结果:
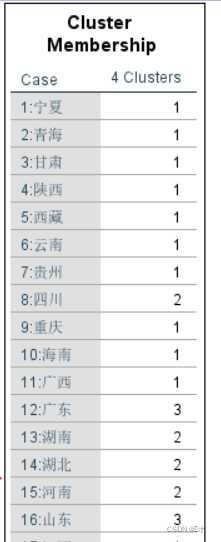
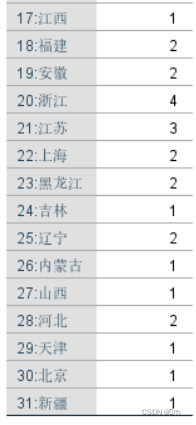
- 分为 4 类。
- 第一类:{北京、天津、山西、内蒙古、吉林、江西、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆}
- 第二类:{河北、辽宁、黑龙江、上海、安徽、福建、河南、湖北、湖南、四川}
- 第三类:{江苏、山东、广东}
- 第四类:{浙江}
文件:地区三大产业产值.sav,给出了31个省、直辖市、自治区的三大产业的生产产值数据,即样品数n=31,变量数p=3。对这31个地区的三大产业发展水平进行K-均值聚类分析,要求分成3类,初始类中心点由SPSS自行指定。
“K-平均值聚类分析”对话框:[Analyze]→[Classify]→[K-Means Cluster Analysis],将“第一产业”、“第二产业”、“第三产业”添加到【Variables】中,将“Region”添加进【Label Cases by】中,并将Number of Clusters更改为3。
在[Save New Variable]对话框中勾选“Cluster membership”和“Distance from cluster center”,将聚类成员和与聚类中心的距离保存到数据集中。
在[Options]选项对话框中选择“Initial cluster centers”和“ANOVA table”两个结果。
结果分析:
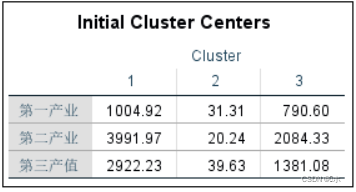
起始聚集中心:每个类的起始类中心的数据(三维坐标)
- 第一类:(1004.92,3991.97,2922.23);
- 第二类:(31.31,20.24,39.63);
- 第三类:(790.60,2084.33,1381.08)。
迭代历程:第1次迭代后,3个类的中心点分别偏移了407.484、647.918、369.044,第1类中心点偏移较大;第2次迭代后,2个类的中心点偏移均小于指定的判定标准(SPSS默认为0.02),聚类分析结束。

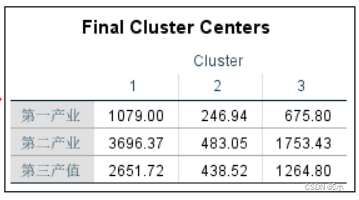
最终聚集中心:每个类的最终类中心的数据(坐标)
- 第一类:(1079.00,3696.37,2651.72);
- 第二类:(246.94,483.05,438.52);
- 第三类:(675.80,1753.43,1264.80);
- 第二类为最优。
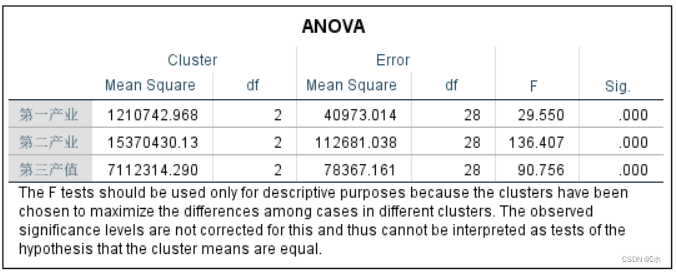
方差分析表:因为各个因子对应的p值=0.000,p值 < α=0.05,所以各因子的均值在类中的差异显著。
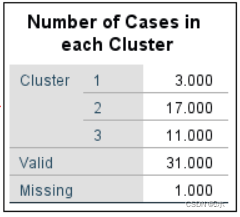
K-均值聚类分析类成员情况:第一类包含3个地区;第二类包含17个地区;第三类包含11个地区。
K-均值聚类分析分类结果:
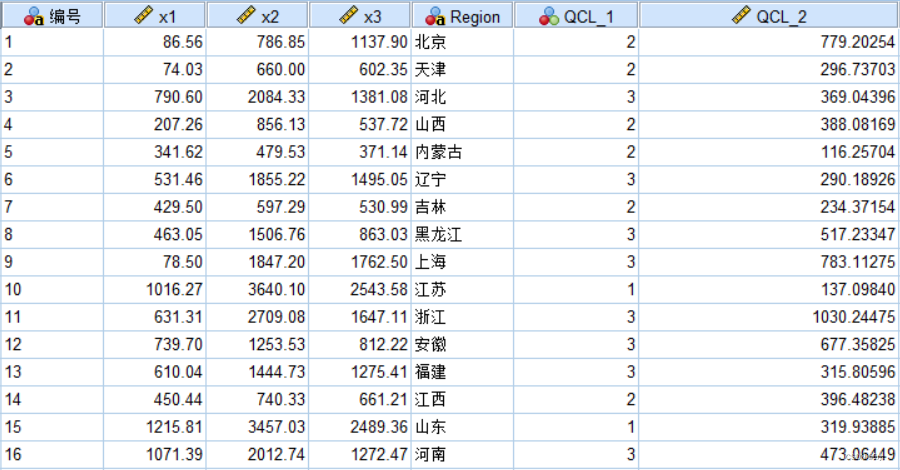
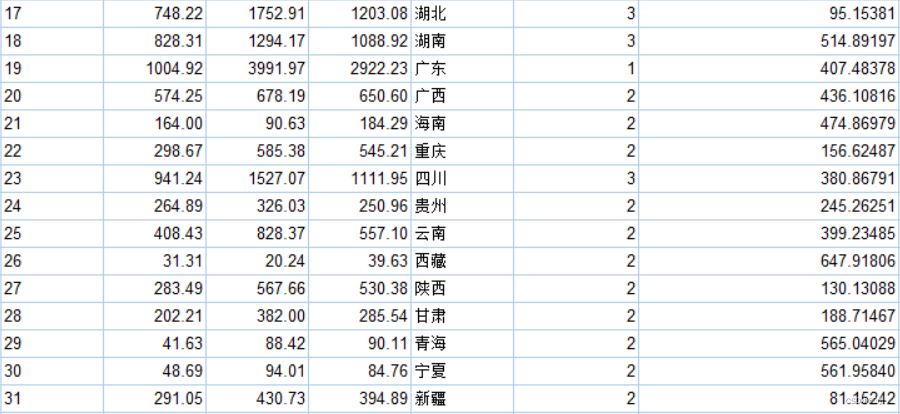
- 结论:分为 3 类。
- 第一类:{江苏、山东、广东}
- 第二类:{北京、天津、山西、内蒙古、吉林、江西、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆}
- 第三类:{河北、辽宁、黑龙江、上海、浙江、安徽、福建、河南、湖北、湖南、四川}
这篇关于SPSS之聚类分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!