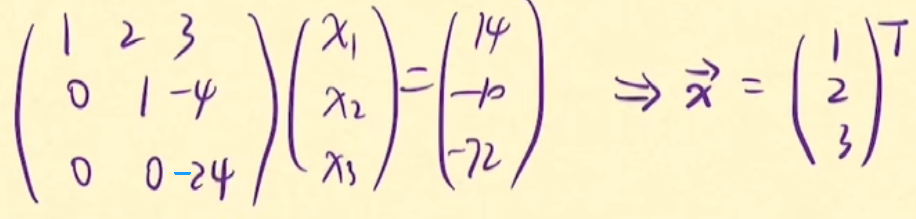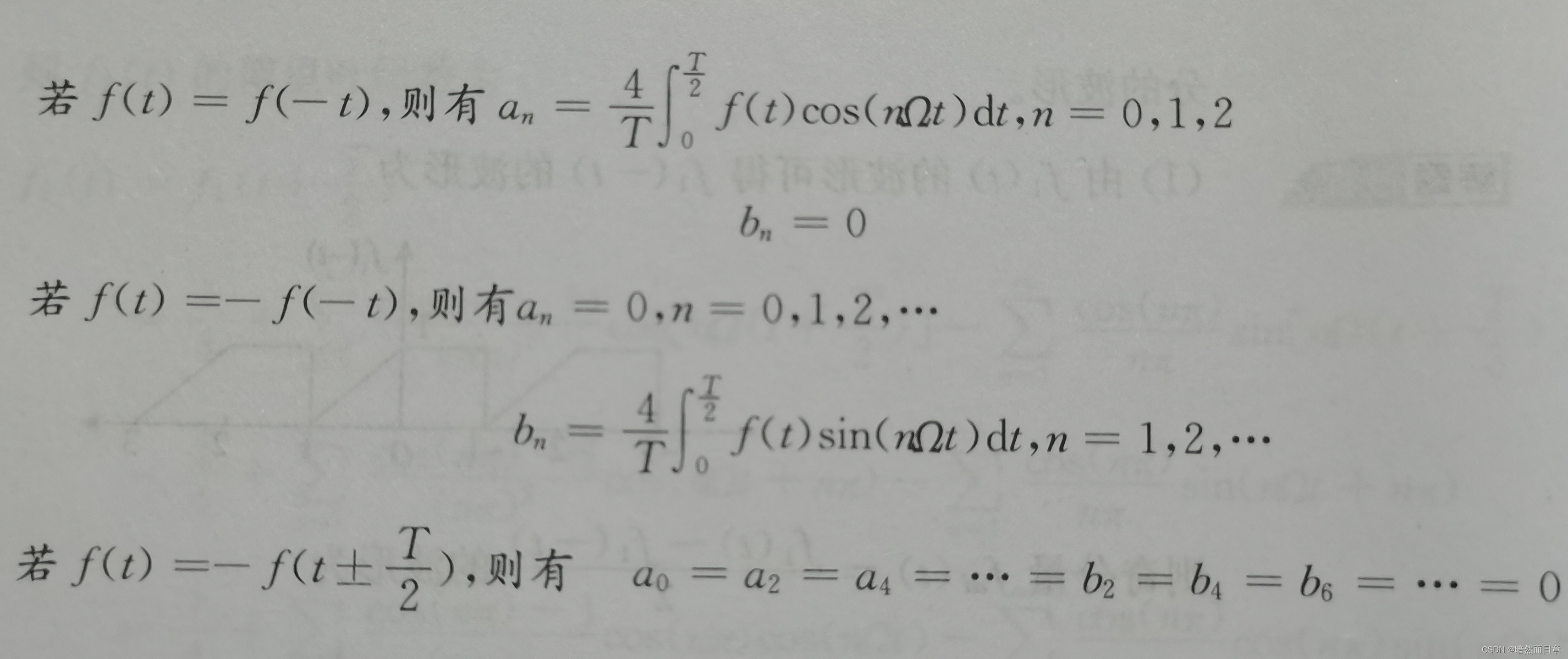线性系统专题
【线性系统理论】笔记二
状态转移矩阵-性质 特殊的矩阵指数函数 A求矩阵指数函数计算 方法1:特征值互异 方法2:特征值重根 方法3:反拉氏变换 方法4: 凯莱-哈密顿求e 特征值互异: 特征值相同 状态转移矩阵e求A 零输入响应 零状态响应 状态运动规律(轨迹) 输出方程的解
【线性系统理论】笔记一
一:状态空间表达式 电路系统状态空间描述列写 1:选取状态变量 状态变量定义:线性无关极大组属性。 2:列出电路原始回路方程 ps:状态变量有两个,理论上需要列写2个方程 3:规范形势 4:导出状态变量方程&输出方程 输出方程直接由电路关系式和状态变量方程得到 得出: MATLAB系统模型转换
系统稳定性判定分析(一)---- 常系数线性系统内部稳定性
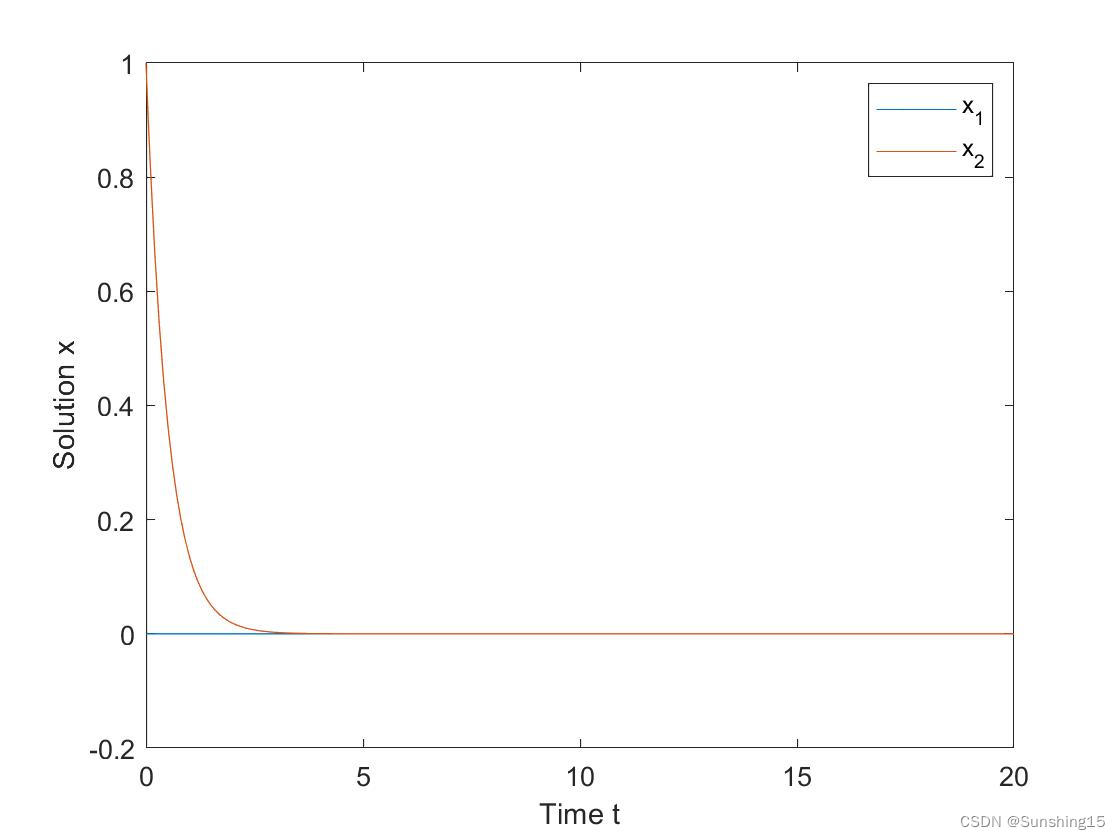
文章目录 线性系统稳定性分析线性定常系统(线性时不变/自治系统)稳定性分析线性定常系统内部稳定性示例 参考文献 从上一节 系统稳定性的介绍中可以得知,分析系统内部稳定(Lyapunov意义下稳定)时可不考虑系统的输出情况,可直接通过系统的状态方程分析系统的稳定性。系统的状态方程根据构建形式的不同,可分为线性系统与非线性系统。如下基于由简入繁的原则,首先整理线性系统的稳定性分析过
矩阵计算-线性系统和 LU 分解
一、三角系统 …… 二、高斯消元法 …… 三、LU分解--直接三角分解法 求解线性方程Ax=b: 参考视频:【数值分析】矩阵LU三角分解| 速成讲解 考试宝典_哔哩哔哩_bilibili 令A=L·U,其中L是单位下三角矩阵(对角线上元素都是1),U是上三角矩阵。 无论矩阵A是多少,都有唯一的单位下三角矩阵L和上三角矩阵U,使得A可以分解为L·U。 由矩阵乘法可
Chapter6.2:线性系统的校正方法
此系列属于胡寿松《自动控制原理题海与考研指导》(第三版)习题精选,仅包含部分经典习题,需要完整版习题答案请自行查找,本系列属于知识点巩固部分,搭配如下几个系列进行学习,可用于期末考试和考研复习。 自动控制原理(第七版)知识提炼 自动控制原理(第七版)课后习题精选 自动控制原理(第七版)附录MATLAB基础 第六章:线性系统的校正方法 Example 6.11 设复合校正控制系统如下图
自动控制原理9.2:线性系统的可控性与可观测性(下)
参考书籍:《自动控制原理》(第七版).胡寿松主编. 《自动控制原理PDF版下载》 2.线性系统的可控性与可观测性 2.6 线性离散时间系统的可控性和可观测性 线性离散系统的可控性和可达性 设线性时变离散时间系统的状态方程为: x ( k + 1 ) = G ( k ) x ( k ) + H ( k ) u ( k ) , k ∈ T k x(k+1)=G(k)x(k)+H(k)
自动控制原理课后习题精选4.1:线性系统的根轨迹法
本专栏是《自动控制原理》(胡寿松)第七版课后习题精选。 第四章:线性系统的根轨迹法 Example 4.1 已知开环零、极点分布如下图所示,概略绘制相应的闭环根轨迹图。 解: Example 4.2 设单位负反馈系统开环传递函数如下, G ( s ) = K s (
非线性系统【八】|线性系统的能观性与能控性
非线性系统【八】|线性系统的能观性与能控性 对于如下系统 X ˙ = A X + B U Y = C X \dot{X} = AX + BU\\ Y=CX X˙=AX+BUY=CX 其中 X X X为状态量, Y Y Y为观测量 能控性 格拉姆矩阵判据 系统完全能控的充要条件是存在常数 T > 0 T>0 T>0,使得矩阵 W c ( 0 , T ) = ∫ 0 T e − A t
【自控实验】1. 线性系统串联超前校正实验
本科课程实验报告,有太多公式和图片了,干脆直接转成图片了 仅分享和记录,不保证全对 串联超前校正实验:频域设计计算(校正装置),时域观察验证(校正结果) 使用matlab中的simulink进行仿真
OpenNL线性系统求解库
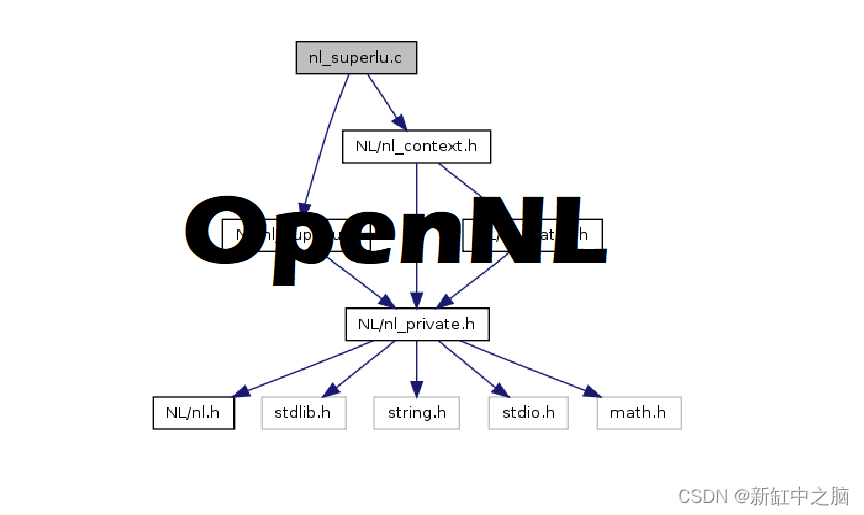
OpenNL 是一个用于求解大型稀疏线性系统的C开发库。 它包括一个易于使用的用于组装矩阵的 API,以及用于对称和非对称系统的各种迭代求解器。 OpenNL API 在 geogram/NL/nl.h 中声明。 NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT
信号与线性系统翻转课堂笔记12——时域取样定理
信号与线性系统翻转课堂笔记12 The Flipped Classroom12 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1)了解信号取样的概念; (2,重点)理想取样信号及其频谱:能利用频域方法,熟练分析理想取样过程及其频谱,掌握理想取样频谱的特点,与原信号频谱的关系以及取样信号频谱不发生混
信号与线性系统翻转课堂笔记9——傅里叶变换概念
信号与线性系统翻转课堂笔记9——傅里叶变换 The Flipped Classroom9 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1,重点)非周期信号频谱(傅里叶变换)的概念及其物理意义,傅里叶变换与傅里叶级数之间的联系和区别; (2,重点)矩形单脉冲频谱的特点和带宽; (3,重点)其他典型
信号与线性系统翻转课堂笔记7——信号正交与傅里叶级数
信号与线性系统翻转课堂笔记7——信号正交与傅里叶级数 The Flipped Classroom7 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1,重点)矢量和函数(信号)的正交分解,理解正交分解的特点及其实用价值; (2)周期信号的傅里叶级数,三角傅里叶级数和指数傅里叶级数及其相互关系; (3
信号与线性系统翻转课堂笔记8——周期信号的频谱
信号与线性系统翻转课堂笔记8——周期性信号的频谱 The Flipped Classroom8 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1,重点)周期信号频谱的概念及其物理意义; (2,重点)周期矩形脉冲频谱的形状和特点,了解取样函数及其特点,掌握周期和脉冲宽度变化对周期矩形脉冲频谱的影响;
信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解
信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解 The Flipped Classroom4 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1)连续LTI系统的微分方程模型及其经典解,了解齐次解+特解的微分方程求解方法; (2)系统响应的分解:掌握自由(固有)响应/强迫响应、瞬
信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解
信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解 The Flipped Classroom4 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1)连续LTI系统的微分方程模型及其经典解,了解齐次解+特解的微分方程求解方法; (2)系统响应的分解:掌握自由(固有)响应/强迫响应、瞬
线性系统理论 -- 降阶观测器的设计
定理: 若系统能观测,且rankC=m,则系统的状态观测器的最小维数是(n-m)。 线性定常时不变系统方程如下(以三阶(n=3)单入单出系统为例,有m=rankC=1): 取变换阵P,有: 对上述系统方程进行线性变换, 得到如下形式: 输出y直接给出。于是状态估计时,只需对 n-m=2 维的、进行估计即可。这就是说,降阶观测器的维数为n-m=2。 降
武汉理工大学855信号与线性系统考研分数线,招生人数,报考统计,考情分析,就业,真题,大纲,参考书,武理工855,博睿泽信息通信考研论坛
武汉理工大学855信号与线性系统考研分数线,招生人数,报考统计,考情分析,就业,真题,大纲,参考书,武理工855,博睿泽信息通信考研论坛 武汉理工大学855信号与线性系统考研分数线,招生人数,报考统计,考情分析,就业,真题,大纲,参考书,武理工855,博睿泽信息通信考研论坛
08_改善性能措施高阶系统动态性能线性系统的稳定性分析
改善二阶系统动态性能的措施 基本措施 测速反馈——增加阻尼比例+微分——提前控制 测速反馈实际增加了系统的阻尼比比例+微分的动态性能计算用零点极点法比例+微分是提前控制(红色e为0时,曲线还未上升到稳态值)(了解) 零点极点法(了解) 高阶系统的阶跃响应及动态性能(了解) 高阶系统单位阶跃响应 Φ ( s ) = M ( s ) D ( s ) = b m s
MATLAB 绘制 SISO 和 MIMO 线性系统的时间和频率响应图
系列文章目录 文章目录 系列文章目录前言一、时间响应二、频率响应三、极点/零点图和根节点四、响应特性五、分析 MIMO 系统六、系统比较七、修改时间轴或频率轴数值`如果觉得内容不错,请点赞、收藏、关注` 前言 本例演示如何绘制 SISO 和 MIMO 线性系统的时间和频率响应图。 一、时间响应 创建线性系统。在本例中,创建一个三阶传递函数。 sys = tf(
以下是一个使用C++实现自定义线性系统的卡尔曼滤波拟合的示例代码:
以下是一个使用C++实现自定义线性系统的卡尔曼滤波拟合的示例代码: #include <iostream>#include <opencv2/opencv.hpp>using namespace std;using namespace cv;int main(){// 初始化卡尔曼滤波器KalmanFilter kf(4, 2, 0);// 状态转移矩阵kf.transitionMatri
现代控制理论—①线性系统的状态空间描述
1-1 状态空间的基本概念 问题提出 – 经典控制理论中,线性定常系统用 常微分方程或传递函 数 描述,这是一种输入输出描述。 – 实际上系统除了输出量这个变量之外,还包含有其他相 互独立的变量,而 微分方程或传递函数 对这些内部的中 间变量是不便描述的。 – 不能完全揭示系统的全部运动状态,这是用 常微分方程 或传递函数 描述一个系统的不足之处 。 控