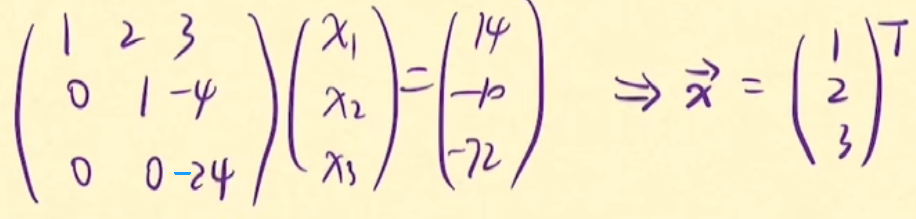本文主要是介绍线性系统(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
线性系统(二)
- 1.直观理解线性方程组结构
- 2. 不同解的结论
- 3. 更一般的高斯-约旦消元法
- 4.齐次线性方程组
链接: 线性系统(一)
1.直观理解线性方程组结构
长这样,方程就有解,即相交坐标。
长这样,没有交点,就没解。
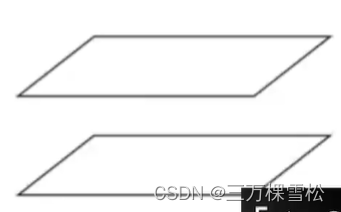
对于两个三元方程联立
长这样就是有解,但没有唯一解,在一条直线上移动。
长这样就是没有解
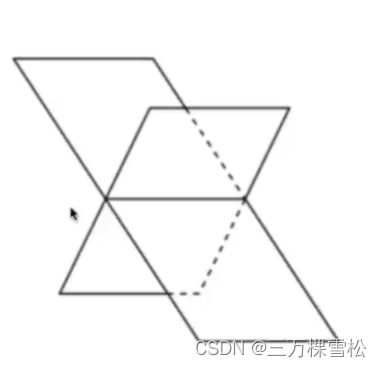
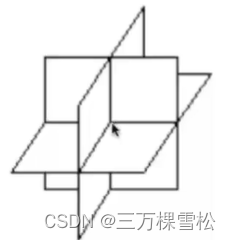
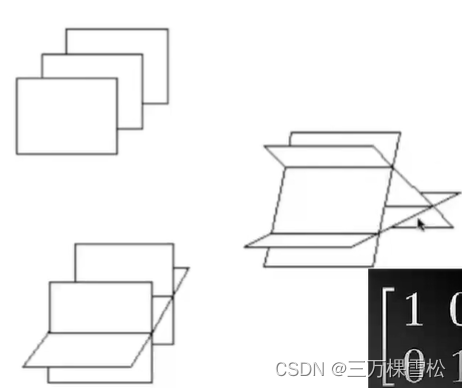
三个三元方程联立
长这样,三个平面交于一点,这样就是唯一解。
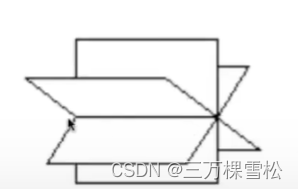
这样就是无数个解,在一条直线上。
长这样,没有满足同时在三个平面上,无解。
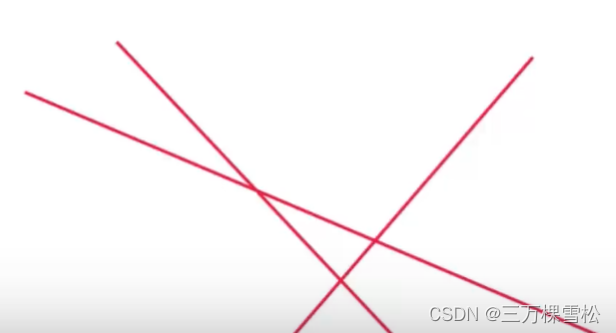
三个二元方程联立
无解
唯一解
无数个解
2. 不同解的结论
1.行最简形式非零行=未知数:唯一解
2.行最简形式非零行<行最简形式非零行:无解
(就是左边000对应右边不是0,有矛盾了)
3.行最简形式非零行<未知数:无数解
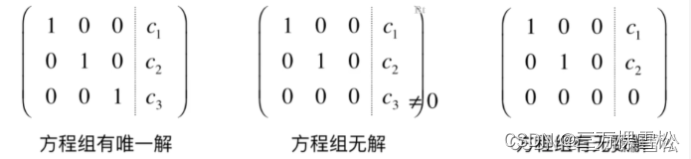
3. 更一般的高斯-约旦消元法

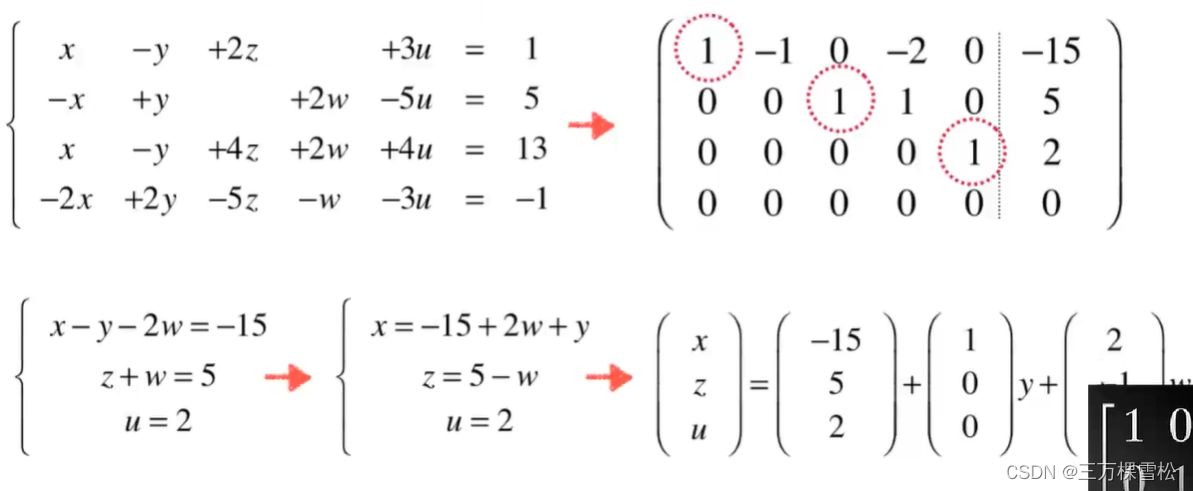
x,z,u根据y,w取值不同而不同。
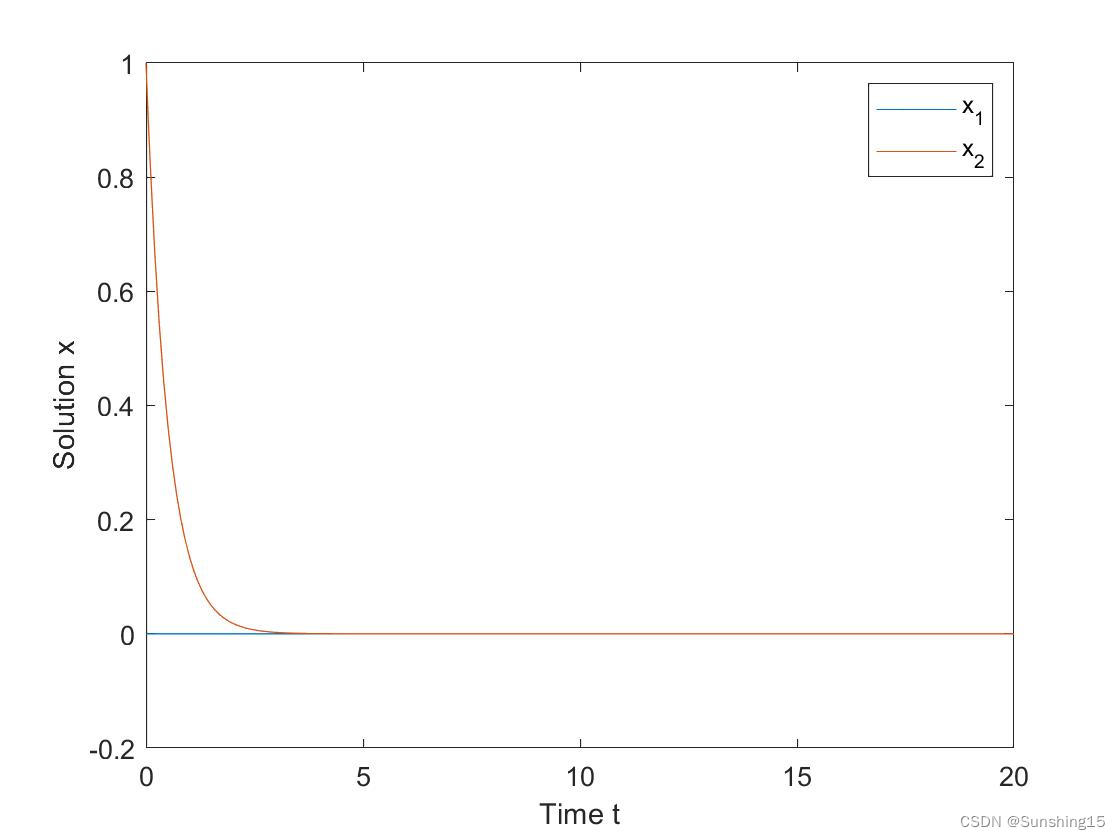
4.齐次线性方程组


这篇关于线性系统(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!