系统稳定性判定分析（一）---- 常系数线性系统内部稳定性

本文主要是介绍系统稳定性判定分析（一）---- 常系数线性系统内部稳定性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

  从上一节 系统稳定性的介绍中可以得知，分析系统内部稳定（Lyapunov意义下稳定）时可不考虑系统的输出情况，可直接通过系统的状态方程分析系统的稳定性。系统的状态方程根据构建形式的不同，可分为线性系统与非线性系统。如下基于由简入繁的原则，首先整理线性系统的稳定性分析过程。

本文内容主要基于Antsaklis, P. J., & Michel, A. N. (1997). Linear systems (Vol. 8). New York: McGraw-Hill. 一书。

线性系统稳定性分析

   ~~~~     线性系统根据状态方程中是否显含时间变量$t$（状态变量本身为时间$t$的函数，因此状态方程一定与时间$t$有关。若状态方程中显示的包含时间$t$的表达式，则表示状态方程显含时间变量$t$。否则，状态方程不显含时间变量$t$），可将线性系统划分为线性自治系统（或线性时不变系统）$$\dot{x}=f(x(t)),\text{\hspace{1em}(1)}$$与线性非自治系统（线性时变系统）$$\dot{x}=f(t,x(t)),\text{\hspace{1em}(2)}$$通常为表述简单，系统 (1) 与 (2) 可直接省略括号内的时间变量$t$，表示为 $\dot{x}=f(x)$ 与 $\dot{x}=f(t,x)$。
   ~~~~     如下首先分析线性自治系统的稳定性。

线性定常系统（线性时不变/自治系统）稳定性分析

   ~~~~     考虑如下线性时不变系统$$\dot{x}=Ax.\text{\hspace{1em}(3)}$$定义 $x_e$ 为系统（3）平衡点，则系统（3）李雅普诺夫意义下的稳定性可通过如下定理进行判定：

定理1. 系统（3）的平衡点 $x_e$ 是稳定的，当且仅当其系数矩阵 $A$ (或者系统（3）的雅可比矩阵) 的所有特征值的实部小于等于0，且每个实部为零的特征值都有一个相关的 1 阶 Jordan 块。系统（3）的平衡点 $x_e$ 是渐近稳定的，当且仅当其系数矩阵 $A$ (或者系统（3）的雅可比矩阵) 的所有特征值的实部小于0。
相反地，系统（3）的平衡点 $x_e$ 是不稳定的，当且仅当其系数矩阵 $A$ (或者其雅可比矩阵) 至少存在一个实部大于0的特征值，或者其实部为零的特征值所对应的Jordan块的阶数大于1阶。

补充： 有关特征值，Jordan块的介绍可参见矩阵分析：特征值，相似度对角化，Jordan标准形。
注： 通常我们所说的一个系统的收敛是与系统平衡点的渐近稳定有关，关于两者有如下定义：

定义1. 系统（3）的平衡点 $x_e$ 是渐近稳定的当且仅当其(1) 是稳定的，(2) 当$t\to \infty$ 时，系统（3）的解趋近于平衡点 $x_e$。

线性定常系统内部稳定性示例

【示例一】分析如下系统在李雅普诺夫意义下的稳定性：
$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].\text{\hspace{1em}(4)}$$通过计算可以得知系统（4）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$，其特征值为${\lambda }_{1,2}=\pm i$，其Jordan块为$\left[\begin{array}{cc}i& 0\\ 0& -i\end{array}\right]$。根据定理1，系统（4）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$是稳定的。系统（4）在初值为（0，0）条件下的运行轨迹如下所示：

系统（4）在初值为（0，1）条件下的运行轨迹如下所示：

结合以上两图可知，系统（4）的平衡点是稳定的，整体运行轨迹在平衡点的一定范围内波动。

【示例二】分析如下系统在李雅普诺夫意义下的稳定性：
$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].\text{\hspace{1em}(5)}$$通过计算可以得知系统（5）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$，其特征值为${\lambda }_{1,2}=0$，其Jordan块为$\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$，特征值0所对应的Jordan块的阶数为2。根据定理1，系统（5）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$是不稳定的。系统（5）在初值为（0，1）条件下的运行轨迹如下所示：

【示例三】分析如下系统在李雅普诺夫意义下的稳定性：
$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}2.8& 9.6\\ 9.6& -2.8\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].\text{\hspace{1em}(6)}$$通过计算可以得知系统（6）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$，其特征值为${\lambda }_{1,2}=\pm 10$，其Jordan块为$\left[\begin{array}{cc}10& 0\\ 0& -10\end{array}\right]$，存在一个实部大于0的特征值。根据定理1，系统（6）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$是不稳定的。系统（6）在初值为（0，1）条件下的运行轨迹如下所示：
【示例四】分析如下系统在李雅普诺夫意义下的稳定性：
$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ -1& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].\text{\hspace{1em}(7)}$$通过计算可以得知系统（7）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$，其特征值为${\lambda }_1=-1$，${\lambda }_2=-2$其Jordan块为$\left[\begin{array}{cc}-1& 0\\ 0& -2\end{array}\right]$，存在一个实部大于0的特征值。根据定理1，系统（7）的平衡点 $x_e=[x_{1e},x_{2e}{]}^T=[0,0{]}^T$是渐近稳定的。系统（7）在初值为（0，1）条件下的运行轨迹如下所示：

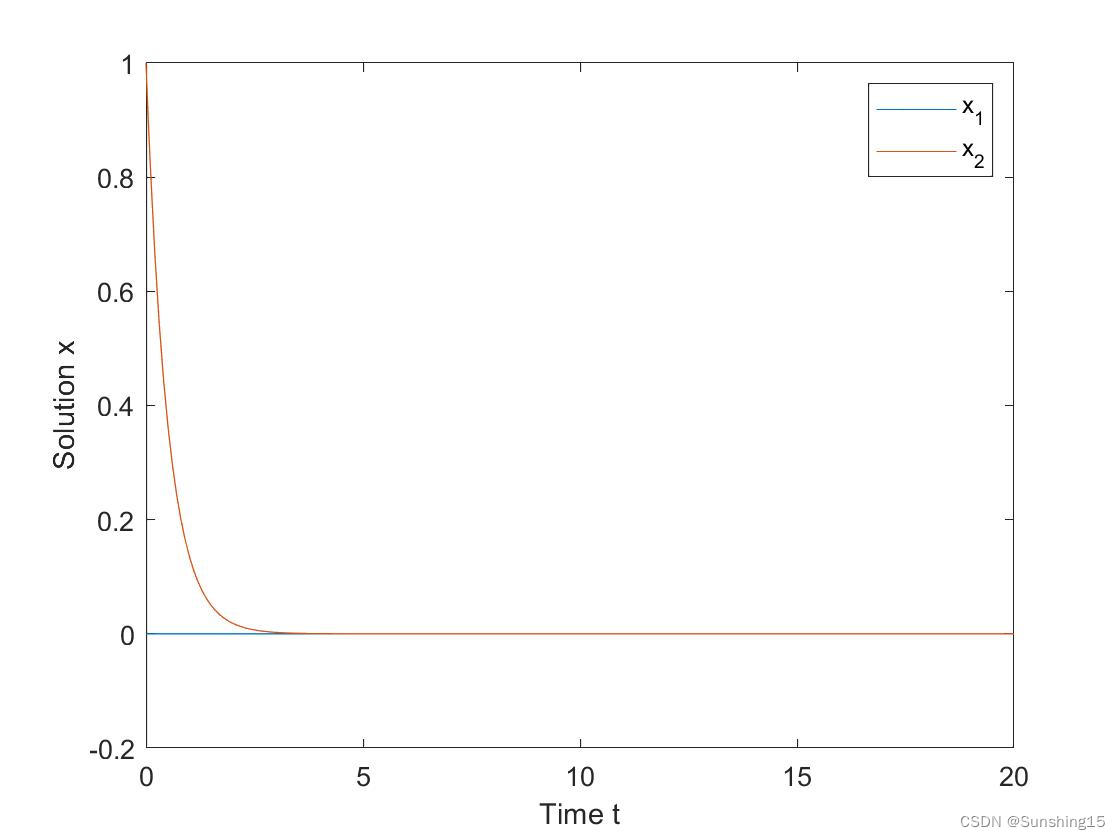
注： 上述四个示例的代码如下，需适当修改函数中的状态方程表达式，以及主函数中的时间变量的区间范围。

function dxdt = vdp1(t,x)%dxdt = [x(2);0];
%  dxdt = [x(2);-x(1)];
% dxdt = [-x(1);-x(1)-2*x(2)]; %dxdt = [x(2);-2*sin(x(1))];dxdt = [2.8*x(1)+9.6*x(2);9.6*x(1)-2.8*x(2)];
end
%[t,y] = ode45(odefun,tspan,y0)
[t,x] = ode45(@vdp1,[0 20],[0,1]);
plot(t,x)
xlabel('Time t');
ylabel('Solution x');
legend('x_1','x_2')

参考文献

[1] Antsaklis, P. J., & Michel, A. N. (1997). Linear systems (Vol. 8). New York: McGraw-Hill.
[2] 线性系统稳定性一般定理、齐次线性系统稳定性
[3] 矩阵分析：特征值，相似度对角化，Jordan标准形

这篇关于系统稳定性判定分析（一）---- 常系数线性系统内部稳定性的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---