本文主要是介绍08_改善性能措施高阶系统动态性能线性系统的稳定性分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
改善二阶系统动态性能的措施
基本措施
- 测速反馈——增加阻尼
- 比例+微分——提前控制




- 测速反馈实际增加了系统的阻尼比
- 比例+微分的动态性能计算用零点极点法
- 比例+微分是提前控制(红色e为0时,曲线还未上升到稳态值)(了解)

零点极点法(了解)


高阶系统的阶跃响应及动态性能(了解)
高阶系统单位阶跃响应
Φ ( s ) = M ( s ) D ( s ) = b m s m + b m − 1 s m − 1 + . . . + b 1 s + b 0 a n n + a n − 1 s n − 1 + . . . a 1 s + a 0 = K ∏ i = 1 m ( s − z i ) ∏ j = 1 n ( s − λ j ) \begin{aligned} \Phi(s)&=\frac{M(s)}{D(s)}=\frac{b_ms^m+b^{m-1}s^{m-1}+...+b_1s+b_0}{a_n^n+a_{n-1}s^{n-1}+...a_1s+a_0}\\ &=\frac{K\prod_{i=1}^m(s-z_i)}{\prod_{j=1}^n(s-\lambda_j)}\\ \end{aligned} Φ(s)=D(s)M(s)=ann+an−1sn−1+...a1s+a0bmsm+bm−1sm−1+...+b1s+b0=∏j=1n(s−λj)K∏i=1m(s−zi)
- 高阶系统的闭环传递函数有多个极点和零点
闭环主导极点
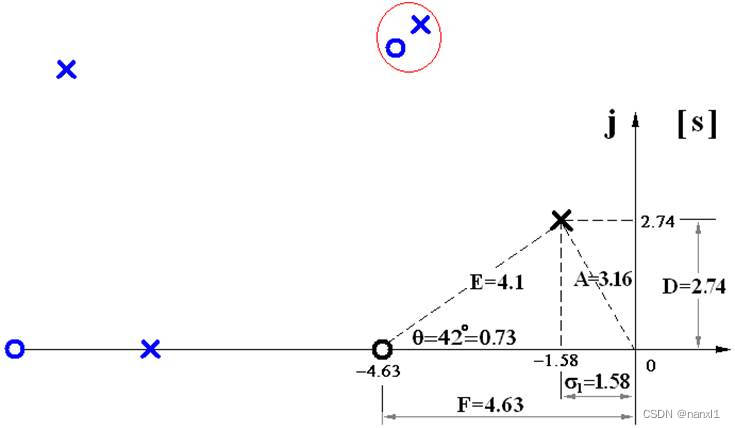
- 主导极点:距离虚轴最近而且附近又没有闭环零点的闭环极点
线性系统的稳定性分析(掌握)
稳定性的概念
- 稳定是控制系统正常工作的首要条件。分析、判定系统的稳定性,并提出确保系统稳定的条件是自动控制理论的基本任务之一。

- 在扰动作用下系统偏离了原来的平衡状态,如果扰动消除后,系统能够以足够的准确度恢复到原来的平衡状态,则系统是稳定的;否则,系统不稳定。
稳定的充要条件(*)
- 若 lim t → ∞ k ( t ) = 0 \lim_{t\rightarrow\infty}k(t)=0 limt→∞k(t)=0,则系统是稳定的
- 系统稳定的充要条件: 系统的所有闭环极点均具有负的实部,或所有闭环极点均严格位于左半s平面
稳定判据(重点)
D ( s ) = a n s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 = 0 ( a n > 0 ) D(s)=a_ns^n+a_{n-1}s^{n-1}+...+a_1s+a_0=0\quad(a_n>0)\\ D(s)=ansn+an−1sn−1+...+a1s+a0=0(an>0)
必要条件: a i > 0 i = 0 , 1 , 2 , . . . , n − 1 a_i>0\qquad i=0,1,2,...,n-1 ai>0i=0,1,2,...,n−1
D ( s ) = s 5 + 6 s 4 + 9 s 3 − 2 s 2 + 8 s + 12 = 0 不稳定 D ( s ) = s 5 + 4 s 4 + 6 s 2 + 9 s + 8 不稳定 ( 缺 s 3 ) D ( s ) = − s 4 − 5 s 3 − 7 s 2 − 2 s − 10 = 0 可能稳定 \begin{aligned} D(s)&=s^5+6s^4+9s^3-2s^2+8s+12=0\qquad不稳定\\ D(s)&=s^5+4s^4+6s^2+9s+8\qquad不稳定(缺s^3)\\ D(s)&=-s^4-5s^3-7s^2-2s-10=0\qquad可能稳定\\ \end{aligned} D(s)D(s)D(s)=s5+6s4+9s3−2s2+8s+12=0不稳定=s5+4s4+6s2+9s+8不稳定(缺s3)=−s4−5s3−7s2−2s−10=0可能稳定
- 满足必要条件的系统只是可能稳定
劳斯判据

劳斯判据特殊情况处理
某行第一列元素为0而该元素行元素不全为0时: 将0改为 ε \varepsilon ε, 继续运算
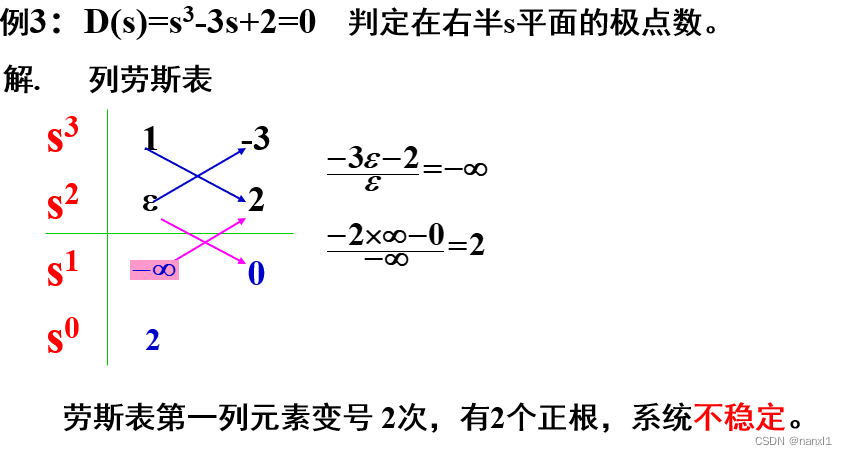
出现全零行时: 用上一行元素组成辅助方程,将其对s求导一次,用新方程的系数代替全零行系数,继续运算


- 出现全零行的系统不稳定
- 辅助方程的解为 D ( s ) = 0 D(s)=0 D(s)=0解的子集
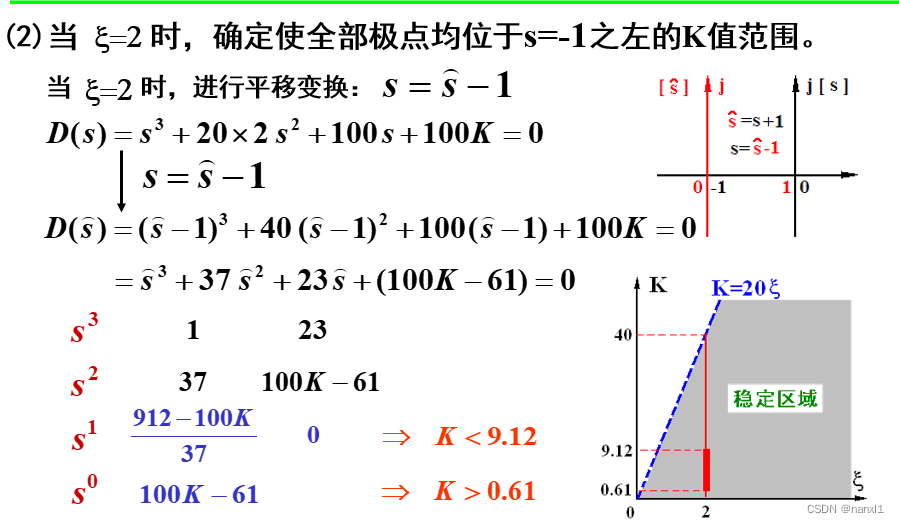
劳斯判据的应用

- 对于二阶系统,当所有系数都大于零时,系统稳定

总结:
- 系统的稳定性是其自身的属性,与输入类型、形式无关。
- 系统稳定与否,只取决于闭环极点,与闭环零点无关
- 闭环零点影响系数Ci ,会改变动态性能,但不影响稳定性。
- 闭环极点决定模态,因此决定系统的稳定性,也影响动态性能。
- 闭环系统的稳定性与其开环是否稳定没有直接关系。
- 改善二阶系统动态性能的措施
- 测速反馈控制——增加阻尼
- 比例+微分控制——提前控制
- 稳定判据
- 判定稳定的必要条件 a i > 0 a_i>0 ai>0
- 劳斯判据
参考资料
【(新版!最清晰!去噪不炸耳!)自动控制原理 西北工业大学 卢京潮】
这篇关于08_改善性能措施高阶系统动态性能线性系统的稳定性分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





