本文主要是介绍信号与线性系统翻转课堂笔记9——傅里叶变换概念,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
信号与线性系统翻转课堂笔记9——傅里叶变换
The Flipped Classroom9 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点)非周期信号频谱(傅里叶变换)的概念及其物理意义,傅里叶变换与傅里叶级数之间的联系和区别;
(2,重点)矩形单脉冲频谱的特点和带宽;
(3,重点)其他典型非周期信号的频谱,需要熟记δ(t)、ε(t)、e^(-αt) ε(t)、符号函数、矩形脉冲等非周期信号的傅里叶变换表达式;
(4,重点)周期信号的傅里叶变换,需要熟记直流信号、 cos(t)、 sin(t)、冲激序列等周期信号的傅里叶变换表达式;
(5)周期信号傅里叶变换与周期信号频谱之间的关系。
二、问题与解答
1、非周期信号的频谱密度(傅里叶变换)与周期信号的频谱(傅里叶系数)之间,存在何种区别和联系?为什么非周期信号的频谱需要用频谱密度来描述?以矩形单脉冲的频谱密度(傅里叶变换)和周期矩形脉冲的频谱(傅里叶系数)为例,说明非周期信号频谱和周期信号频谱的特点(相同点和不同点)。
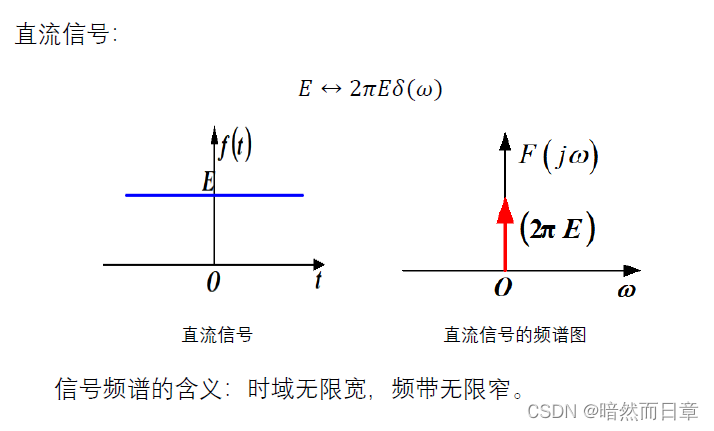
2、非周期信号频谱的物理意义是什么?分别画出δ(t)、 cos(t)和直流信号的频谱(傅里叶变换),基于频谱的物理意义,解释这三个信号频谱的含义。
3、简述求符号函数 sgn( t)频谱的思路和方法。符号函数、阶跃函数和直流信号频谱之间有什么联系?
4、周期信号的频谱和频谱密度之间是何种关系?以周期矩形脉冲为例,说明如果已知周期矩形脉冲的频谱(傅里叶系数),如何求其傅里叶变换?
5、设有一个周期信号f(t),f_0 (t)是截取f(t)的一个周期所构成的单脉冲信号(对应f(t)在原点附近的一个周期),请分别列出周期信号f(t)的傅里叶系数的计算公式和非周期信号f_0 (t)的傅里叶变换的定义式,分析它们之间的联系,得出利用单脉冲的傅里叶变换来求傅里叶系数的公式(已知f_0 (t)的傅里叶变换,如何直接求得f(t)的傅里叶系数)。并以周期单位冲激序列为例,验证所得到公式的正确性。
1、非周期信号傅里叶变换&周期信号傅里叶系数
非周期信号的频谱密度(傅里叶变换)与周期信号的频谱(傅里叶系数)之间,存在何种区别和联系?(第一问)为什么非周期信号的频谱需要用频谱密度来描述?(第二问)以矩形单脉冲的频谱密度(傅里叶变换)和周期矩形脉冲的频谱(傅里叶系数)为例,说明非周期信号频谱和周期信号频谱的特点(相同点和不同点)。(第三问)
(1)

(2)
因为当周期T趋近于无限大时,相邻谱线的间隔Ω趋近于无穷小,谱系数趋近于0,离散谱成为连续谱。各频率分量的幅度也都趋近于无穷小,难以用Fn直观描述信号的频谱,但n不同时其相对大小仍可以区别,所以引入频谱密度概念。
(3)
相同点:
非周期矩形脉冲的频谱(密度)与周期矩形脉冲的频谱包络波形相同;
非周期矩形脉冲的傅里叶变换为实数,与周期矩形脉冲一样,其幅度频谱和相位频谱可以合二为一;
脉冲宽度与带宽成反比。
不同点:
非周期矩形脉冲的频谱密度为连续函数,而周期矩形脉冲的频谱只在离散点具有非零谱线;
两者在物理含义上有本质区别:周期信号表示成傅里叶系数形式,对应的频率分量的系数就是该频率分量的具体幅值。而非周期信号借鉴了傅里叶系数的推导方式,将周期推广到了无穷大,得到了傅里叶变换,傅里叶变换得到的是频谱密度函数,每个频率点对应的数值并不是信号在该频率上分量的实际幅值;必须要除以信号的周期(即无穷大)才是实际幅值,所以可以说非周期信号在任意频率分量上的幅值都是零。
2、非周期信号频谱的物理意义与实例
非周期信号频谱的物理意义是什么?分别画出δ(t)、 cos(t)和直流信号的频谱(傅里叶变换),基于频谱的物理意义,解释这三个信号频谱的含义。



3、求符号函数频谱
简述求符号函数 sgn(t)频谱的思路和方法。符号函数、阶跃函数和直流信号频谱之间有什么联系?



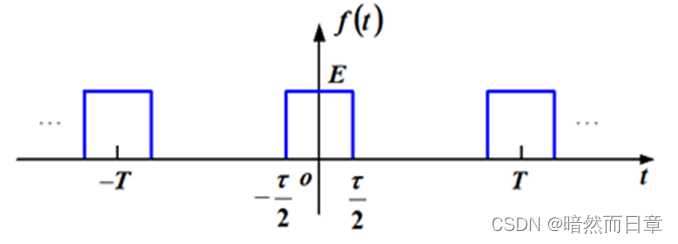
4、周期信号的频谱与频谱密度
周期信号的频谱和频谱密度之间是何种关系?以周期矩形脉冲为例,说明如果已知周期矩形脉冲的频谱(傅里叶系数),如何求其傅里叶变换?

周期矩形脉冲:

5、周期脉冲信号傅里叶系数&单脉冲信号傅里叶变换
设有一个周期信号f(t),f_0 (t)是截取f(t)的一个周期所构成的单脉冲信号(对应f(t)在原点附近的一个周期),请分别列出周期信号f(t)的傅里叶系数的计算公式和非周期信号f_0 (t)的傅里叶变换的定义式,分析它们之间的联系,得出利用单脉冲的傅里叶变换来求傅里叶系数的公式(已知f_0 (t)的傅里叶变换,如何直接求得f(t)的傅里叶系数)。并以周期单位冲激序列为例,验证所得到公式的正确性。


三、反思总结
暂无
这篇关于信号与线性系统翻转课堂笔记9——傅里叶变换概念的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








