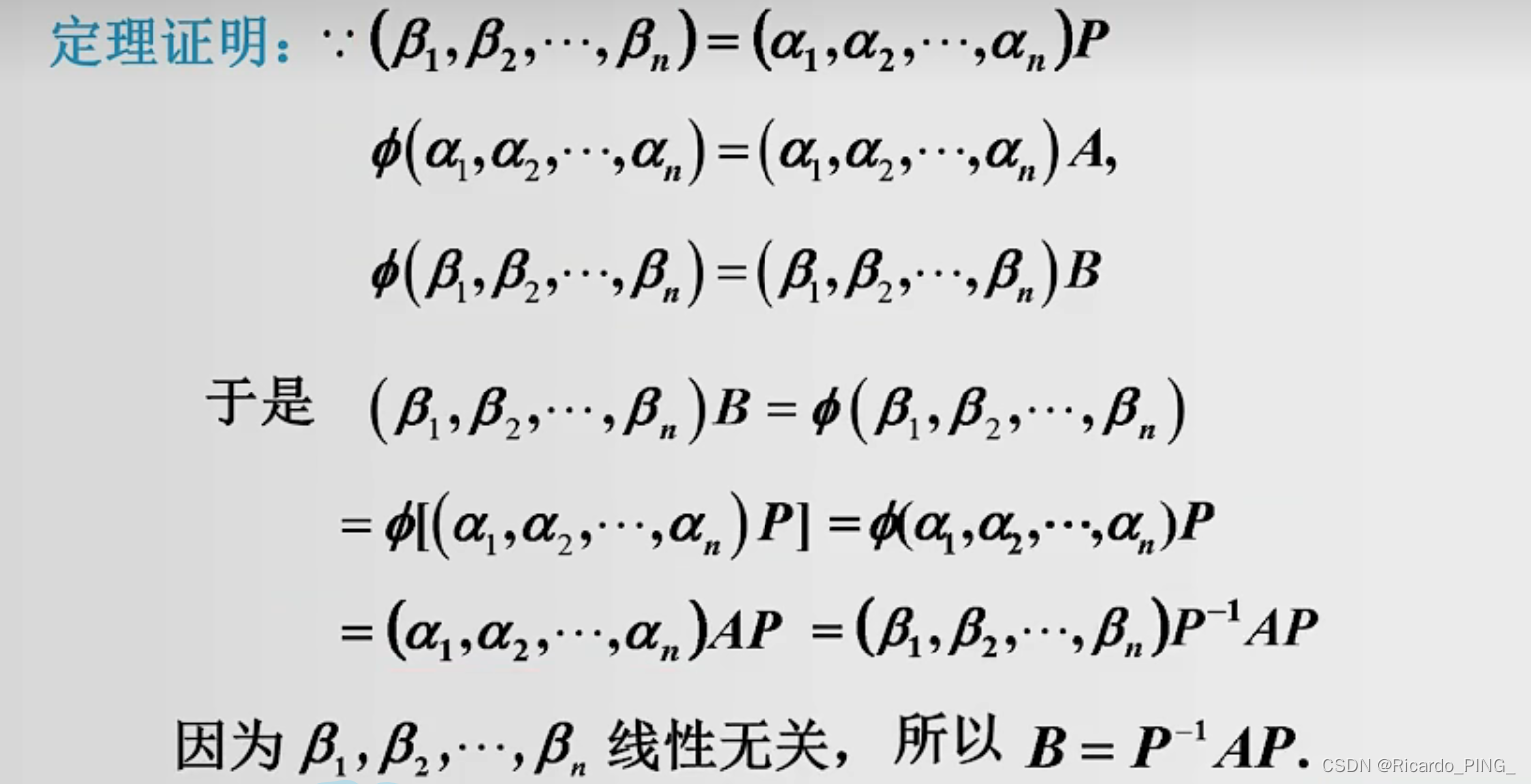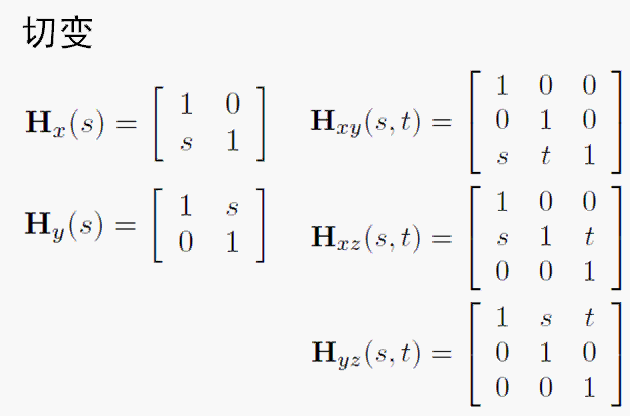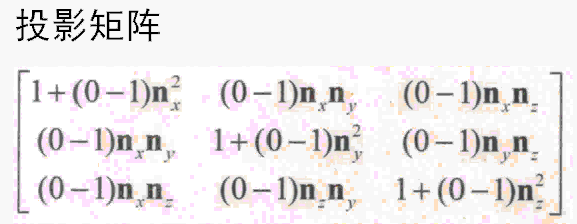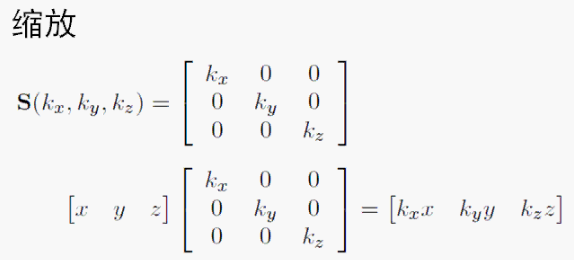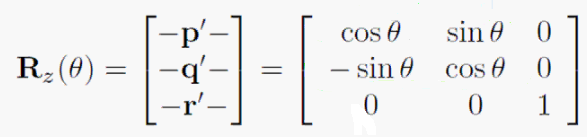线性变换专题
opencv中灰度线性变换问题
近来在读《数字图像处理与机器视觉——Visual C++与Matlab实现》,(该书下载地址:http://pan.baidu.com/share/link?shareid=3551301329&uk=1610854122)想把里面的例子用opencv的方法都去实现一下,读到69页中关于灰度线性变换,直接在refman中按关键字“linear transformation”去查找,找到 C: v
3D数学基础--矩阵线性变换
前言 本章主要讨论用3×3矩阵表达3D线性变换,这个变换不包括平移,包含平移的变换称作仿射变换(就是线性变换后接着平移),需要用4×4矩阵表达。所以本章所讨论的变换都是基于坐标系原点的变换。 旋转 2D中的旋转:因暂不考虑平移,假设物体绕原点旋转,我们通常规定逆时针旋转为正方向,顺时针为负方向(不是必须)。得到的2D旋转矩阵如下图所示: 3D中绕坐标轴旋转:同样讨论前需先明确正方向,左手坐
深度学习中的子空间、线性变换和矩阵概念应用
1.表示子空间 在深度学习中,“不同的表示子空间”通常是指模型通过不同的参数(例如权重矩阵)将输入数据映射到不同的高维空间,这些空间被称为表示子空间。每个子空间都能够捕获输入数据中不同的特征或模式。以下是一些详细解释: 1. 特征表示: 在机器学习中,特征表示是指数据在某个空间中的表示形式。一个模型的目的是找到一个良好的特征表示,使得数据中的模式和关系能够被容易地
【矩阵论】12——线性变换——线性变换矩阵的对角化
本系列文章由Titus_1996 原创,转载请注明出处。 文章链接:https://blog.csdn.net/Titus_1996/article/details/83177967 本系列文章使用的教材为《矩阵论》(第二版),杨明,刘先忠编,华中科技大学出版社。 一个线性变换在空间不同基下的矩阵构成一个相似类。对于T能否有基使他在该基下矩阵为对角阵的问题转化为矩阵等否相似于对角阵的
【矩阵论】11——Jordan标准型——线性变换的特征值与特征向量
本系列文章由Titus_1996 原创,转载请注明出处。 文章链接:https://blog.csdn.net/Titus_1996/article/details/83177254 本系列文章使用的教材为《矩阵论》(第二版),杨明,刘先忠编,华中科技大学出版社。 定义 假设T在某组基{α1,α2,...αn}下的矩阵为A,ξ是T关于λ的特征向量。则有 ξ=(α1,α2,..
【矩阵论】10——线性变换——同一数域不同线性空间的线性变换
本系列文章由Titus_1996 原创,转载请注明出处。 文章链接:https://blog.csdn.net/Titus_1996/article/details/83148139 本系列文章使用的教材为《矩阵论》(第二版),杨明,刘先忠编,华中科技大学出版社。 概念 总结: 线性空间的线性变换在同一数域 Vn中的原像通过T作用,像在Vm中。 变换是线性的,
[矩阵分析] 一、线性空间与线性变换
目录 线性空间及其性质 定义 关键性质 1. 封闭性 2. 加法运算的性质 3. 标量乘法的性质 4. 线性组合、跨度和线性独立性 5. 子空间、基和维数 6. 核和像 核(Kernel) 像(Image) 核与像的关系 应用 一些重要的性质 通俗理解 线性空间的维数、基与坐标 维数 (Dimension) 基 (Basis) 坐标 (Coordinates)
[笔记][总结] MIT线性代数 Gilbert Strang 线性变换和基变换
作者水平有限,欢迎大家提出文中错误 线性变换和基变换 基本概念基线性变换 矩阵如何描述线性变换坐标与基线性变换的矩阵表示 线性变换的几何图像恒等变换 I I I拉伸/压缩变换剪切变换 E E E旋转变换 R R R单位正交矩阵 R R R 投影矩阵秩的含义 矩阵乘法的意义逆变换与矩阵积的求逆法则 基变换再议相似性特征基和对角化 基本概念 基 设 V V V是数域 K K K
矩阵分析与计算学习记录-线性空间和线性变换
本章知识要点 线性空间:维数、基、坐标、基变换、坐标变换、线性相关线性无关,极大线性无关组、范德蒙德行列式; 线性空间的分解:子空间、值域(像空间)与核空间(零空间)、 秩与零度、子空间的交、和与直和; 线性变换及其矩阵表示:定义、运算、值域与核空间、秩 与零度、相似类、特征值与特征向量、不变子空间、同构。 首先这里介绍数域的概念 设P是由一些复数组成的集合,其中包括0与1,如果P中任意
《矩阵论》学习笔记(一):第一章 线性空间与线性变换
《矩阵论》学习笔记:第一章 线性空间与线性变换 文章目录 《矩阵论》学习笔记:第一章 线性空间与线性变换一、线性空间1.1 线性空间1.2 线性变换及其矩阵1.2.1 线性变换及其应用1.2.2 线性变换的矩阵表示1.2.3 特征值和特征向量1.2.4 对角矩阵1.2.6 jordan标准型 1.3 两个特殊的线性空间1.3.1 欧氏空间1.3.2 酉空间 二、线性变换及其性质
线性代数学习笔记(二):线性变换的理解
线性代数学习笔记(二):线性变换的理解 文章目录 线性代数学习笔记(二):线性变换的理解一、基变换与坐标变换二、 线性变换2.1 线性变换与基变换的不同2.2 线性变换的表示2.3 线性变换的分类2.4 线性变换与矩阵2.5 应用:线性代数观点看线性变换2.5.1 微分方程是线性变换2.5.2 傅里叶变换是基底变换2.5.3 相似矩阵 三、线性空间的理解四、矩阵的理解 一、基
【矩阵论笔记】线性变换的零空间与值空间(包括一般方法)
定义 零空间的维度是线性变换T的零度 值空间的维度是线性变换T的秩 求线性变换的零空间和值空间 1、先找个矩阵A出来 2、A和线性变换的零空间和值空间一样。 求零空间和值空间的一般方法 例子
3D数学 矩阵和线性变换之切变
矩阵和线性变换之切变 1. 什么是切变? 我们来看一幅图片。下面的图片,随着y增大,x的偏移会越来越大。这种类型的变换就叫切换。我们可以得到下图的公式x’ = x + sy。该公式转换成矩阵就得到了切变矩阵。 2. 切变效果的矩阵是怎样的? 在3D中,同样的道理,有如下右边三个矩阵,分别是随着z增大,x和y发生切变。随着y增大,x和z发生切变。随着z增大,x和y发生切变。
3D数学 矩阵和线性变换之镜像
矩阵和线性变换之镜像 1. 什么是镜像变换? 在2D中镜像变换就如下图所示,沿着某条轴发生对称现象就叫镜像变换。在3D中同理可以得到沿着某个平面发生对称的现象。 2. 镜像变换的矩阵是怎样的? 我们想来看简单的,沿着x轴、y轴或z轴发生镜像变换(注意是“沿着”轴的镜像,而不是“关于”轴对称),原理很简单,只需要让x、y或z变为相反数即可。所以我们分别只需令单位矩阵上第一列、第二
3D数学 矩阵和线性变换之正交投影
矩阵和线性变换之正交投影 1. 具有正交投影效果的矩阵是怎样的? 这里给出一个正交投影在法向量(而且同时又是单位向量)为(x,y,z)平面上的投影矩阵,数学证明暂时不说,详见《3d数学基础 图形与游戏开发》。 2. 投影矩阵编程示例 void Matrix3X3::setOrthProject(Vector3 &vec){assert(fabs(vec*vec) - 1 < 0
3D数学 矩阵和线性变换之缩放
矩阵和线性变换之缩放 1. 具有缩放效果的矩阵是怎样的? 我们这里只做沿着x、y、z轴方向的缩放,至于沿着任意方向的缩放比较复杂而且也很少用,所以暂时不介绍。如下图所示,原理非常简单,x、y、z乘上对应的缩放系数kx,ky,kz就得到了缩放后的结果。 2. 缩放矩阵编程示例 void Matrix3X3::setScale(Vector3& vec){m11 = vec.x;
3D数学 矩阵和线性变换之旋转
矩阵和线性变换之旋转 1. 如何在3D世界中对坐标进行变换? 我们可以通过产生一个具有某种变换效果的矩形,用坐标上的某个点乘上这个矩阵,就会得到变换后的点。这是线性代数中线性变换的内容。 2. 具有旋转效果的矩阵如何生成? 首先说明下,这本书里用的都是左手坐标系。我们规定左手坐标系,拇指朝向旋转轴,其他手指的方向就是旋转的正方向。 通过线性变换的数学推理,可以得到, 绕X轴
【ML学习笔记】4:机器学习中的数学基础4(线性变换的矩阵描述)
线性空间 线性空间即向量空间,如果空间中有一个原点O,那么空间中的所有点都可以用向量来表示,这些向量及其运算构成的即是向量空间。 基 基是线性空间里的一组向量,使得该线性空间中任何一个向量都可以唯一表示成这组基的线性组合。 如则(a,b)就是P点在这个线性空间下以X向量和Y向量为基的坐标。 要成为基要满足一些条件,首先这些向量要属于这个线性空间: 并且这些向量v1…vk线性无关,而
位姿变换线性变换与坐标变换
位姿,线性变换与坐标变换.yuque 内旋,外旋, 左乘,右乘很容易把人绕晕是因为缺少一种科学的符号。 自己的符号,如果经常变不稳定,对推理和理解都很不利。 一旦问题复杂起来, 直观和直觉靠不住, 只能靠代数符号来推理 约定 P1: A,B,C…是空间中的标准正交基 P2: [a1,a2,…an] 是系A的基, [b1,b2,…bn] 是系B的基,其中aj 和bj 都是n维列向量 一个坐标系可以
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(10):线性变换定义
目录 前言往期文章3.1 线性变换定义定义3.1 :线性变换定义3.2定理3.1.1定理3.1.2定义3.3定义3.4定义3.5定义3.6 结语 前言 Hello!小伙伴! 非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~ 自我介绍 ଘ(੭ˊᵕˋ)੭ 昵称:海轰 标签:程序猿|C++选手|学生 简介:因C语言结识编程,随后转入计算机专业,有幸拿过一些国奖、省
【线性代数的本质 - 系列合集】04 矩阵乘法与线性变换复合的联系(万字详文)
兄弟们,没看过视频的先滚去看视频!!!笔记是用来复习的 课程是blibli和youtube上的: 线性代数的本质 - 系列合集 Linear transformations and matrices | Chapter 3, Essence of linear algebra 嘿 大家好! 上期视频结束前 我展示了线性变换长什么样,以及如何用矩阵描述它们 这值得我们快速回顾一下,因
04-附注 三维空间中的线性变换
附注 三维空间中的线性变换 三维空间线性变换 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 三维空间线性变换 图1 绕y轴旋转90° 绕y轴旋转90°后,各基向量所在的坐标如图1所示。用旋转后的各基向量作为矩阵的列,就得到变换矩阵。变换矩阵就是对原向量就是缩放、旋转。
04 矩阵乘法与线性变换复合
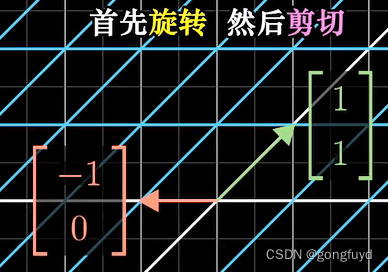
矩阵乘法与线性变换复合 复合变换 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 复合变换 图1 复合变换 复合变换原则,依次变换,即先变换的矩阵乘待变换的向量后,得到的结果,再用后变换的矩阵乘此结果向量。从矩阵角度描述,即先变换对应的矩阵M1在后变换对应矩阵M2的右侧。 注意:相继两次变换,顺序不同,得到的结果不同。比如,先逆时针旋转90°,再剪
03 矩阵与线性变换
矩阵与线性变换 线性变换如何用数值描述线性变换特殊的线性变换反过来看总结 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 线性变换 如果一个变换具有以下两个性质,我们就称它是线性的: 一是直线在变换后仍然保持为直线二是原点必须保持固定 总的来说,线性变换是“保持网格线平行且等距分布”的变换 如何用数值描述线性变换 只需记录两个基向量 i ⃗ \vec






![[笔记][总结] MIT线性代数 Gilbert Strang 线性变换和基变换](https://img-blog.csdnimg.cn/20200318100546121.gif)