本文主要是介绍[笔记][总结] MIT线性代数 Gilbert Strang 线性变换和基变换,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者水平有限,欢迎大家提出文中错误
线性变换和基变换
- 基本概念
- 基
- 线性变换
- 矩阵如何描述线性变换
- 坐标与基
- 线性变换的矩阵表示
- 线性变换的几何图像
- 恒等变换 I I I
- 拉伸/压缩变换
- 剪切变换 E E E
- 旋转变换 R R R
- 投影矩阵
- 秩的含义
- 矩阵乘法的意义
- 逆变换与矩阵积的求逆法则
- 基变换
- 再议相似性
- 特征基和对角化
基本概念
基
设 V V V是数域 K K K上的线性空间, x 1 , x 2 , ⋯ , x r ∈ V x_1,x_2,\cdots,x_r \in V x1,x2,⋯,xr∈V,若 x 1 , x 2 , ⋯ , x r x_1,x_2,\cdots,x_r x1,x2,⋯,xr可以
- x 1 , x 2 , ⋯ , x r x_1,x_2,\cdots,x_r x1,x2,⋯,xr线性无关
- s p a n { x 1 , x 2 , ⋯ , x r } = V span\{x_1,x_2,\cdots,x_r\}=V span{x1,x2,⋯,xr}=V
称 x 1 , x 2 , ⋯ , x r x_1,x_2,\cdots,x_r x1,x2,⋯,xr是 V V V的一组基
线性变换
如果数域 K K K上有线性空间 V V V的一个变换 T T T具有下列性质:
T ( k x + l y ) = k T ( x ) + l T ( y ) , x , y ∈ V ; k , l ∈ K T(kx+ly)=kT(x)+lT(y),x,y\in V;k,l\in K T(kx+ly)=kT(x)+lT(y),x,y∈V;k,l∈K
则称 T T T是 V V V的一个线性变换或线性算子
- 投影变换是线性变换
- 平移变换不是线性变换
- T ( v ) = ∣ ∣ v ∣ ∣ T(v)=\left| |v| \right| T(v)=∣∣v∣∣不是线性变换
- 以原点为轴的旋转是线性变换
- 导数算符是一种线性算子
矩阵如何描述线性变换
坐标与基
显然 A ( ⋅ ) A(\cdot) A(⋅)是一个线性变换
但是矩阵 A A A如何描述一个变换呢?
T ( v ) = A v T(v)=Av T(v)=Av
矩阵 A m ∗ n A_{m*n} Am∗n,描述了线性变换 T ( ∗ ) : ℜ n → ℜ m T(*):\ \real^n\rightarrow\real^m T(∗): ℜn→ℜm(只考虑矩阵右乘)
T ( v 1 ) T(v_1) T(v1)可以描述线性变换对向量 v 1 v_1 v1的操作
T ( v 2 ) T(v_2) T(v2)可以描述线性变换对向量 v 2 v_2 v2的操作
如果假设两向量线性无关,那么就可以知道 T T T对 v 1 v_1 v1和 v 2 v_2 v2张成的整个空间的操作
所以我们如果有 T ( v 1 ) ⋯ T ( v n ) T(v_1)\cdots T(v_n) T(v1)⋯T(vn), v 1 ⋯ v n v_1\cdots v_n v1⋯vn构成了输入空间 R n \mathbb R^n Rn的一组基。那么整个线性变换就完全掌握了。
对于输入空间中的任意一个向量均有
v = c 1 v 1 + c 2 v 2 + ⋯ + c n v n v=c_1v_1+c_2v_2+\cdots+c_nv_n v=c1v1+c2v2+⋯+cnvn
T ( v ) = c 1 T ( v 1 ) + c 2 T ( v 2 ) + ⋯ + c n T ( v n ) T(v)=c_1T(v_1)+c_2T(v_2)+\cdots+c_nT(v_n) T(v)=c1T(v1)+c2T(v2)+⋯+cnT(vn)
可见如果空间中的一组基被确定了,那么向量 v v v的表示也就被唯一确定了
c 1 ⋯ c n c_1\cdots c_n c1⋯cn被称为向量 v v v在基 v 1 ⋯ v n v_1\cdots v_n v1⋯vn下的坐标值,坐标来源于基,而线性变换和向量本身于坐标无关
线性变换的矩阵表示
如果想通过矩阵确定一个线性变换,还缺什么
选取输入空间 R n \mathbb R^n Rn一组基 v 1 ⋯ v n v_1\cdots v_n v1⋯vn,输出空间 R m \mathbb R^m Rm的一组基 w 1 ⋯ w m w_1\cdots w_m w1⋯wm
T ( v ) = c 1 T ( v 1 ) + c 2 T ( v 2 ) + ⋯ + c n T ( v n ) = T(v)=c_1T(v_1)+c_2T(v_2)+\cdots+c_nT(v_n)= T(v)=c1T(v1)+c2T(v2)+⋯+cnT(vn)=
[ T ( v 1 ) T ( v 2 ) ⋯ T ( v n ) ] [ c 1 c 2 ⋮ c n ] [T(v_1)\ T(v_2)\cdots T(v_n)] \left[ \begin{matrix} c_1\\ c_2\\ \vdots\\ c_n \end{matrix} \right] [T(v1) T(v2)⋯T(vn)]⎣⎢⎢⎢⎡c1c2⋮cn⎦⎥⎥⎥⎤
[ T ( v 1 ) T ( v 2 ) ⋯ T ( v n ) ] [T(v_1)\ T(v_2)\cdots T(v_n)] [T(v1) T(v2)⋯T(vn)]描述了这个线性变换
T ( v i ) T(v_i) T(vi)是输出空间 R m \mathbb R^m Rm的一个向量,在基 w 1 ⋯ w m w_1\cdots w_m w1⋯wm下它有一组坐标值为基 a 1 i ⋯ a m i a_{1i}\cdots a_{mi} a1i⋯ami
[ T ( v 1 ) T ( v 2 ) ⋯ T ( v n ) ] = [ w 1 w 2 ⋯ w m ] [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [T(v_1)\ T(v_2)\cdots T(v_n)]=[w_1\ w_2\cdots w_m] \left[ \begin{matrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{matrix} \right] [T(v1) T(v2)⋯T(vn)]=[w1 w2⋯wm]⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎦⎥⎥⎥⎤
假设输出向量为 w = T ( v ) w=T(v) w=T(v)
w = b 1 w 1 + b 2 w 2 + ⋯ + b m w m = [ w 1 w 2 ⋯ w m ] [ b 1 b 2 ⋮ b m ] w=b_1w_1+b_2w_2+\cdots+b_mw_m=[w_1 w_2\cdots w_m] \left[ \begin{matrix} b_1\\ b_2\\ \vdots\\ b_m \end{matrix} \right] w=b1w1+b2w2+⋯+bmwm=[w1w2⋯wm]⎣⎢⎢⎢⎡b1b2⋮bm⎦⎥⎥⎥⎤
最后
[ w 1 w 2 ⋯ w m ] [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ c 1 c 2 ⋮ c n ] = [ w 1 w 2 ⋯ w m ] [ b 1 b 2 ⋮ b m ] [w_1\ w_2\cdots w_m] \left[ \begin{matrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{matrix} \right] \left[ \begin{matrix} c_1\\ c_2\\ \vdots\\ c_n \end{matrix} \right]= [w_1 w_2\cdots w_m] \left[ \begin{matrix} b_1\\ b_2\\ \vdots\\ b_m \end{matrix} \right] [w1 w2⋯wm]⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡c1c2⋮cn⎦⎥⎥⎥⎤=[w1w2⋯wm]⎣⎢⎢⎢⎡b1b2⋮bm⎦⎥⎥⎥⎤
[ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ c 1 c 2 ⋮ c n ] = [ b 1 b 2 ⋮ b m ] \left[ \begin{matrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{matrix} \right] \left[ \begin{matrix} c_1\\ c_2\\ \vdots\\ c_n \end{matrix} \right]= \left[ \begin{matrix} b_1\\ b_2\\ \vdots\\ b_m \end{matrix} \right] ⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡c1c2⋮cn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡b1b2⋮bm⎦⎥⎥⎥⎤
A c = b Ac=b Ac=b
A A A在基 v 1 ⋯ v n v_1\cdots v_n v1⋯vn和 w 1 ⋯ w m w_1\cdots w_m w1⋯wm下描述了线性变换, c c c是向量 v v v的坐标, b b b是向量 w = T ( v ) w=T(v) w=T(v)的坐标。
总之,矩阵 A A A的各列是输入空间各基经过线性变换后,在输出空间的一组基下的坐标
线性变换的几何图像
接下来,看一下 R 3 \mathbb R^3 R3空间的变换,在 R 3 \mathbb R^3 R3空间放置一个单位立方体,观察其在线性变化下的变化

恒等变换 I I I
[ 1 0 0 0 1 0 0 0 1 ] \left[ \begin{matrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{matrix} \right] ⎣⎡100010001⎦⎤
在恒等变换下,所有向量均映射到自身,单位立方体不变

拉伸/压缩变换
[ a 0 0 0 1 0 0 0 1 ] \left[ \begin{matrix} a&0&0\\ 0&1&0\\ 0&0&1 \end{matrix} \right] ⎣⎡a00010001⎦⎤
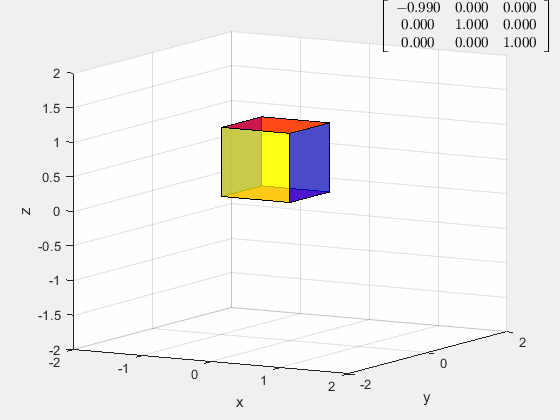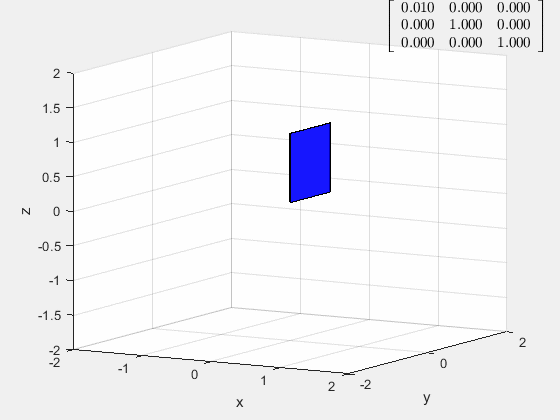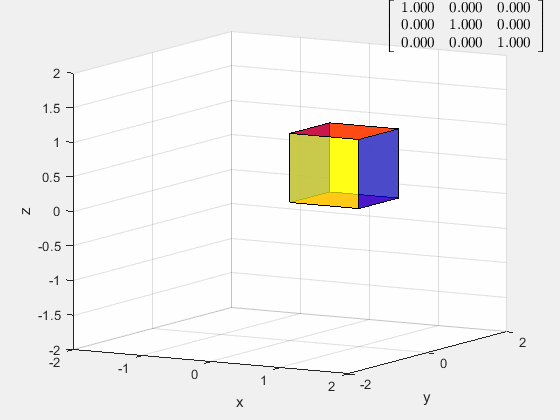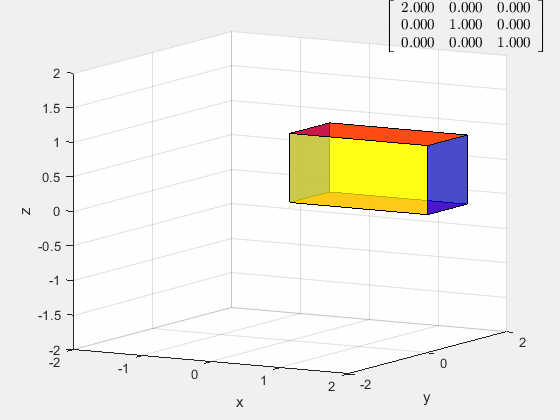
一维拉伸/压缩变换对应的是行/列倍乘矩阵,可见当 0 < a < 1 0<a<1 0<a<1的时候为压缩变换, a a a为压缩比;当 a > 1 a>1 a>1的时候,为拉伸变换, a a a为拉伸比。
而当 a < 0 a<0 a<0的时候,为坐标面的镜像变换,和拉伸变换的合变换。
剪切变换 E E E
[ 1 0 0 0 1 0 a 0 1 ] \left[ \begin{matrix} 1&0&0\\ 0&1&0\\ a&0&1 \end{matrix} \right] ⎣⎡10a010001⎦⎤
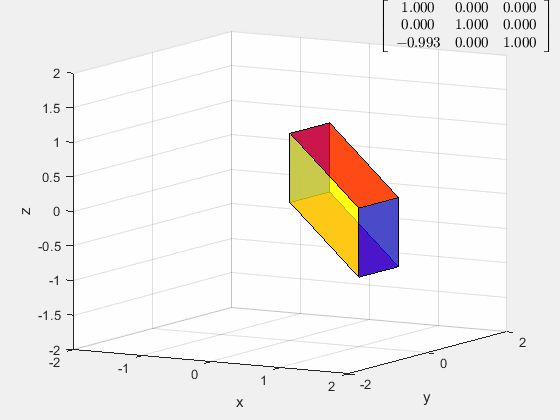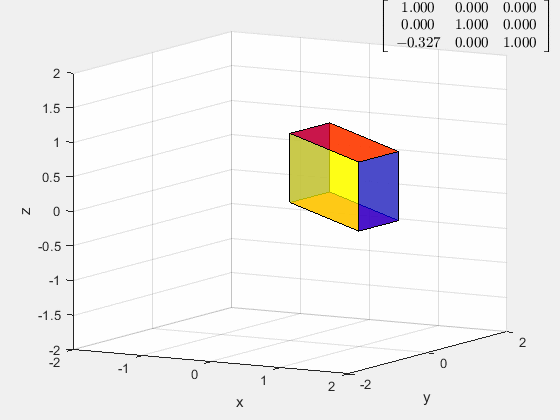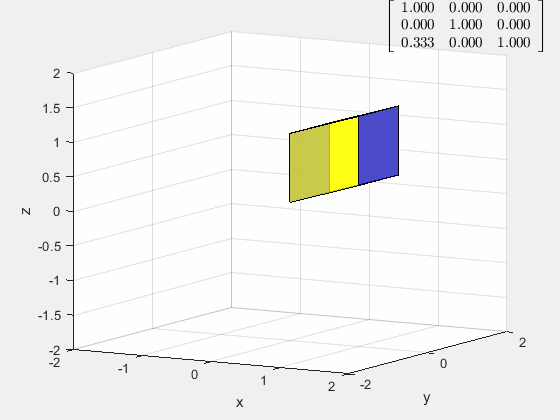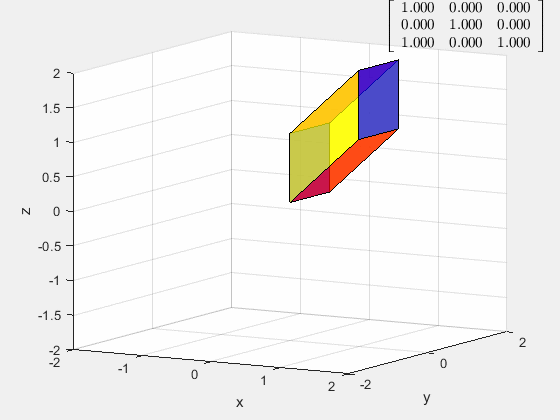
剪切变换对应的是行/列倍加矩阵
旋转变换 R R R
角速度在 x x x轴方向的旋转
[ 1 0 0 0 c o s θ − s i n θ 0 s i n θ c o s θ ] \left[ \begin{matrix} 1&0&0\\ 0&cos\theta & -sin\theta \\ 0&sin\theta &cos\theta \end{matrix} \right] ⎣⎡1000cosθsinθ0−sinθcosθ⎦⎤
右下角的二阶子方阵为二维的旋转矩阵

角速度在 y y y轴方向的旋转
[ c o s θ 0 s i n θ 0 1 0 − s i n θ 0 c o s θ ] \left[ \begin{matrix} cos\theta& 0&sin\theta\\ 0& 1& 0\\ -sin\theta &0&cos\theta \end{matrix} \right] ⎣⎡cosθ0−sinθ010sinθ0cosθ⎦⎤
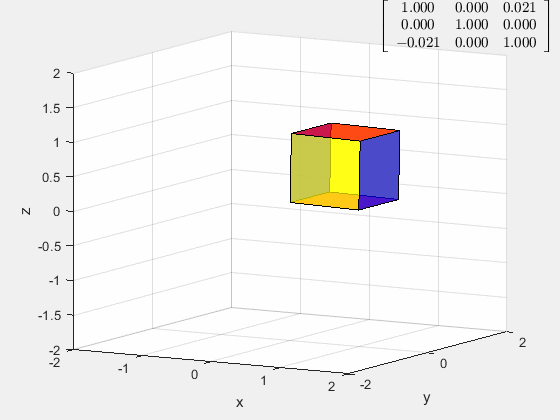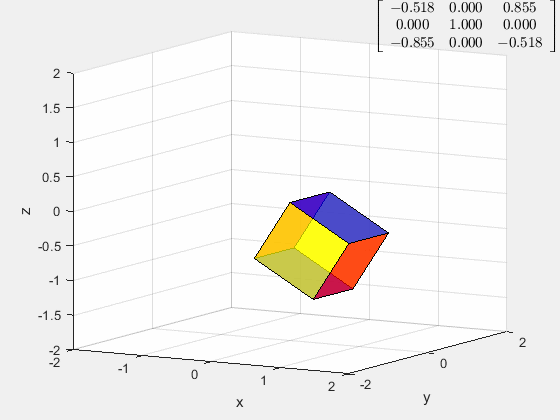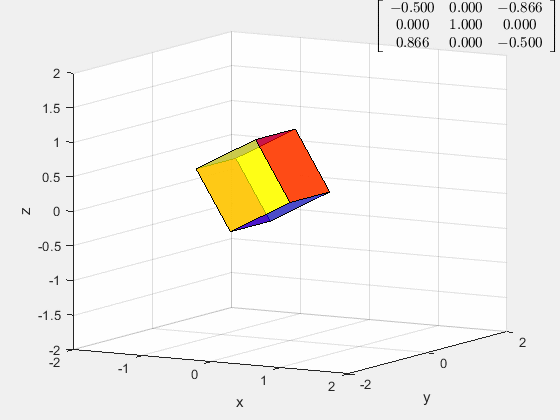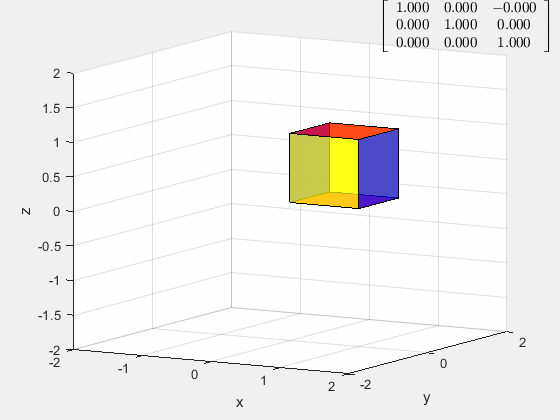
角速度在 z z z轴方向上的旋转
[ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] \left[ \begin{matrix} cos\theta& -sin\theta&0\\ sin\theta& cos\theta&0\\ 0&0&1 \end{matrix} \right] ⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤

其他所有旋转都可以由这三种旋转组合生成
单位正交矩阵 R R R
旋转矩阵都是单位正交矩阵,但是除了单位正交矩阵,单位正交矩阵对应的线性变换还有恒等变换,镜像变换。
正交矩阵则是个更大的家族,允许对向量的长度进行拉伸或压缩。
投影矩阵
下面有向量场,是 z = x 2 + y 2 z=x^2+y^2 z=x2+y2的梯度场(将向量分布于平面 z = x − y z=x-y z=x−y上),如何把 ∇ z \nabla z ∇z投影到平面 z = x − y z=x-y z=x−y上?


投影矩阵
A ( A T A ) − 1 A T A(A^TA)^{-1}A^T A(ATA)−1AT
下面的问题是如何确定 A A A, C ( A ) = { v ∣ v 3 = v 1 − v 2 } C(A)=\{v|v_3=v_1-v_2\} C(A)={v∣v3=v1−v2}
随便找两个平面上的不线性相关的向量,组成矩阵
A = [ 1 0 0 1 1 − 1 ] A= \left[ \begin{matrix} 1&0\\ 0&1\\ 1&-1 \end{matrix} \right] A=⎣⎡10101−1⎦⎤
构造投影矩阵
P = A ( A T A ) − 1 A T = [ 2 / 3 1 / 3 1 / 3 1 / 3 2 / 3 − 1 / 3 1 / 3 − 1 / 3 2 / 3 ] P=A(A^TA)^{-1}A^T= \left[ \begin{matrix} 2/3&1/3&1/3\\ 1/3&2/3&-1/3\\ 1/3&-1/3&2/3 \end{matrix} \right] P=A(ATA)−1AT=⎣⎡2/31/31/31/32/3−1/31/3−1/32/3⎦⎤
P P P左乘向量场中各向量后


秩的含义
矩阵的秩在线性变换中代表着变换后的空间的维数,如上面的投影矩阵,秩为2,而线性变换后的输出空间也为2(但是注意,输出空间还在 R 3 \mathbb R^3 R3中)。
矩阵乘法的意义
矩阵乘法其实是依照一定次序的线性变换的合变换。

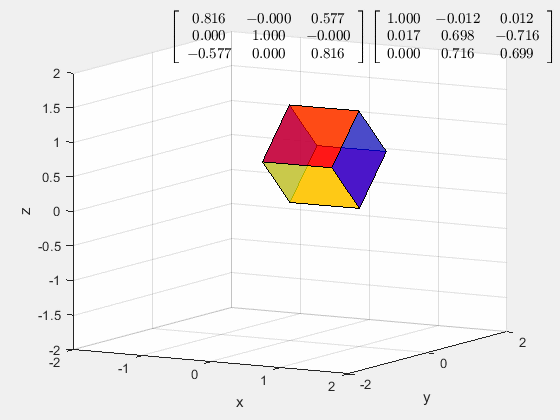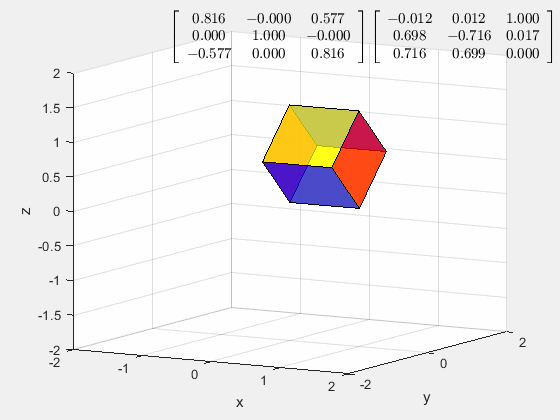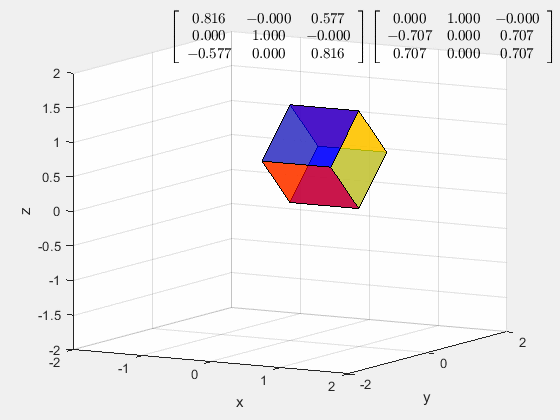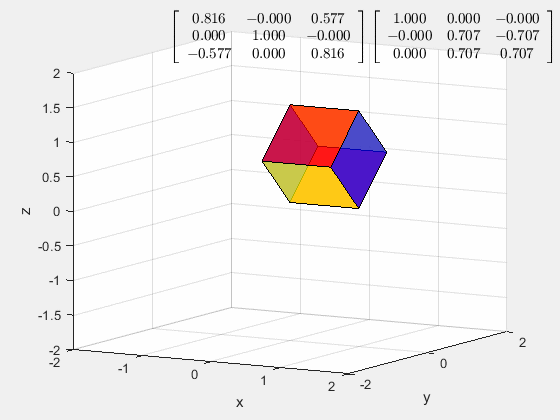
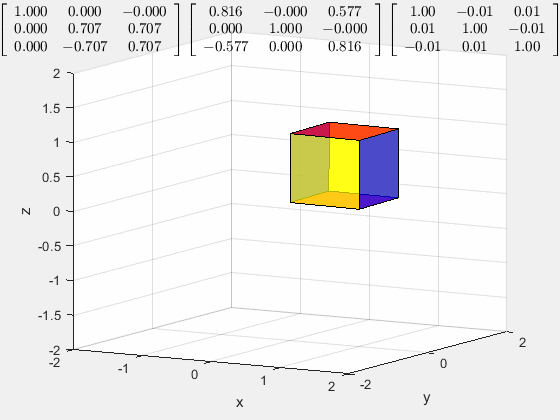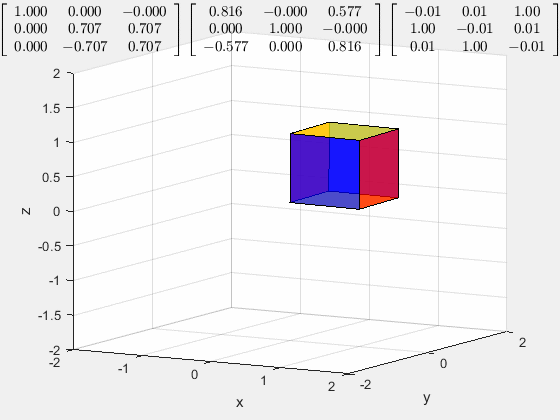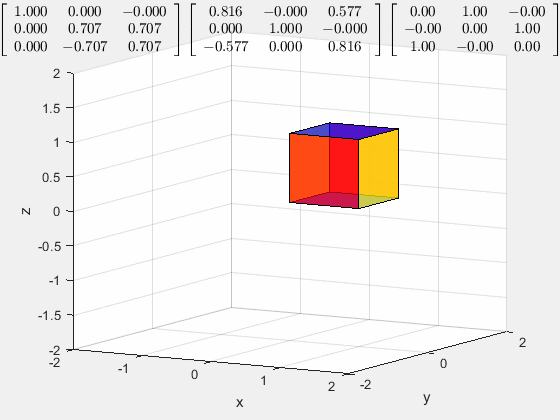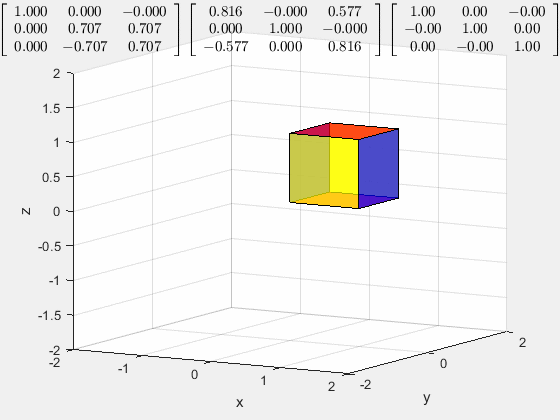
这样的旋转是怎么生成的?
它是把立方体的空间对角线旋转至与 z z z轴重合,然后进行 z z z轴的旋转
首先,以 x x x轴为轴旋转 45 ° 45\degree 45°,将一条棱放在 x O z xOz xOz做表面上

然后以 y y y轴为轴旋转 − a r c t a n ( 1 2 ) r a d -arctan(\frac{1}{\sqrt 2})\ rad −arctan(21) rad

然后乘以 z z z轴的旋转矩阵

如果上面的三个矩阵交换次序是无法得出一样得结果的,这是从几何意义上讲为什么矩阵乘法不能交换次序。
逆变换与矩阵积的求逆法则
A − 1 A = I A^{-1}A=I A−1A=I,经过矩阵和其逆的共同作用,一切恢复了原样(恒等变换),矩阵逆代表的是其逆变换
接着上面的例子,如果想将对角线恢复到原来的位置,但是保持旋转,需要做什么
记得最开始在施加旋转效果之前,有两个常旋转矩阵,只需要按步骤依次将这两个矩阵消除即可。
所以首先,以 y y y轴为轴旋转 a r c t a n ( 1 2 ) r a d arctan(\frac{1}{\sqrt 2})\ rad arctan(21) rad
然后以 x x x轴为轴旋转 − 45 ° -45\degree −45°
( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
这个道理就像俄罗斯套娃,必须把外层的先打开,才能继续打开里面的
基变换
在本文开头,已经知道一个线性变换只有在基给定的情况下,矩阵才能描述一个线性变换,但是对于同一线性变换,不同基的形式之间有什么联系?
先考虑一个向量 v v v在不同的基下,坐标之间有什么联系
假设旧基为 x 1 x 2 ⋯ x n x_1\ x_2\cdots x_n x1 x2⋯xn,这组基下 v v v的坐标为 α 1 α 2 ⋯ α n \alpha_1\ \alpha_2\cdots \alpha_n α1 α2⋯αn,新基为 y 1 y 2 ⋯ y n y_1\ y_2\cdots y_n y1 y2⋯yn,这组基下 v v v的坐标为 β 1 β 2 ⋯ β n \beta_1\ \beta_2\cdots \beta_n β1 β2⋯βn
v = α 1 x 1 + α 2 x 2 + ⋯ + α n x n = β 1 y 1 + β 2 y 2 + ⋯ + β n y n v=\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n=\beta_1y_1+\beta_2y_2+\cdots+\beta_ny_n v=α1x1+α2x2+⋯+αnxn=β1y1+β2y2+⋯+βnyn
v = [ x 1 x 2 ⋯ x n ] [ α 1 α 2 ⋮ α n ] = [ y 1 y 2 ⋯ y n ] [ β 1 β 2 ⋮ β n ] v=\left[x_1\ x_2\cdots x_n\right] \left[ \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right]= \left[y_1\ y_2\cdots y_n\right] \left[ \begin{matrix} \beta_1\\ \beta_2\\ \vdots\\ \beta_n \end{matrix} \right] v=[x1 x2⋯xn]⎣⎢⎢⎢⎡α1α2⋮αn⎦⎥⎥⎥⎤=[y1 y2⋯yn]⎣⎢⎢⎢⎡β1β2⋮βn⎦⎥⎥⎥⎤
假设 y i y_i yi的 x 1 x 2 ⋯ x n x_1\ x_2\cdots x_n x1 x2⋯xn线性表示为
y i = w i 1 x i + w i 2 x i + ⋯ + w i n x i y_i=w_{i1}x_i+w_{i2}x_i+\cdots +w_{in}x_i yi=wi1xi+wi2xi+⋯+winxi
[ x 1 x 2 ⋯ x n ] [ w 11 w 12 ⋯ w 1 n w 21 w 22 ⋯ w 2 n ⋮ ⋮ ⋱ ⋮ w n 1 w n 2 ⋯ w n n ] = [ y 1 y 2 ⋯ y n ] [x_1\ x_2\cdots x_n] \left[ \begin{matrix} w_{11}&w_{12}&\cdots &w_{1n}\\ w_{21}&w_{22}&\cdots &w_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ w_{n1}&w_{n2}&\cdots &w_{nn}\\ \end{matrix} \right]= [y_1 y_2\cdots y_n] [x1 x2⋯xn]⎣⎢⎢⎢⎡w11w21⋮wn1w12w22⋮wn2⋯⋯⋱⋯w1nw2n⋮wnn⎦⎥⎥⎥⎤=[y1y2⋯yn]
v = [ x 1 x 2 ⋯ x n ] [ α 1 α 2 ⋮ α n ] = [ x 1 x 2 ⋯ x n ] [ w 11 w 12 ⋯ w 1 n w 21 w 22 ⋯ w 2 n ⋮ ⋮ ⋱ ⋮ w n 1 w n 2 ⋯ w n n ] [ β 1 β 2 ⋮ β n ] v=\left[x_1\ x_2\cdots x_n\right] \left[ \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right]= [x_1\ x_2\cdots x_n] \left[ \begin{matrix} w_{11}&w_{12}&\cdots &w_{1n}\\ w_{21}&w_{22}&\cdots &w_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ w_{n1}&w_{n2}&\cdots &w_{nn}\\ \end{matrix} \right] \left[ \begin{matrix} \beta_1\\ \beta_2\\ \vdots\\ \beta_n \end{matrix} \right] v=[x1 x2⋯xn]⎣⎢⎢⎢⎡α1α2⋮αn⎦⎥⎥⎥⎤=[x1 x2⋯xn]⎣⎢⎢⎢⎡w11w21⋮wn1w12w22⋮wn2⋯⋯⋱⋯w1nw2n⋮wnn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡β1β2⋮βn⎦⎥⎥⎥⎤
[ α 1 α 2 ⋮ α n ] = [ w 11 w 12 ⋯ w 1 n w 21 w 22 ⋯ w 2 n ⋮ ⋮ ⋱ ⋮ w n 1 w n 2 ⋯ w n n ] [ β 1 β 2 ⋮ β n ] \left[ \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right]= \left[ \begin{matrix} w_{11}&w_{12}&\cdots &w_{1n}\\ w_{21}&w_{22}&\cdots &w_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ w_{n1}&w_{n2}&\cdots &w_{nn}\\ \end{matrix} \right] \left[ \begin{matrix} \beta_1\\ \beta_2\\ \vdots\\ \beta_n \end{matrix} \right] ⎣⎢⎢⎢⎡α1α2⋮αn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡w11w21⋮wn1w12w22⋮wn2⋯⋯⋱⋯w1nw2n⋮wnn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡β1β2⋮βn⎦⎥⎥⎥⎤
α = W β \alpha=W\beta α=Wβ
综上,如果新基等于旧基和旧基关系如下
[ y 1 y 2 ⋯ y n ] = [ x 1 x 2 ⋯ x n ] W [y_1\ y_2\cdots y_n]=[x_1\ x_2\cdots x_n]W [y1 y2⋯yn]=[x1 x2⋯xn]W
上式称为基变换
如果 v v v
在基 y 1 y 2 ⋯ y n y_1\ y_2\cdots y_n y1 y2⋯yn的坐标为 β 1 β 2 ⋯ β n \beta_1\ \beta_2\cdots \beta_n β1 β2⋯βn,
在基 x 1 x 2 ⋯ x n x_1\ x_2\cdots x_n x1 x2⋯xn的坐标为 α 1 α 2 ⋯ α n \alpha_1\ \alpha_2\cdots \alpha_n α1 α2⋯αn
那么两组坐标的关系是
α = W β \alpha=W\beta α=Wβ
或表示成
[ v ] x = W [ v ] y [v]_x=W[v]_y [v]x=W[v]y
称为坐标变换, W W W称为过渡矩阵
再议相似性
回到本节最开始的问题,在不同的基下,相同线性变换的矩阵有什么联系?
首先应该重申一下,相似矩阵是方阵中的概念
方阵就意味着输入空间和输出空间是同一个空间
有基变换
[ y 1 y 2 ⋯ y n ] = [ x 1 x 2 ⋯ x n ] W [y_1\ y_2\cdots y_n]=[x_1\ x_2\cdots x_n]W [y1 y2⋯yn]=[x1 x2⋯xn]W
向量 v v v的坐标变换为
α = W β \alpha=W\beta α=Wβ
向量 T ( v ) T(v) T(v)的坐标变换为
γ = W δ \gamma=W\delta γ=Wδ
线性变换矩阵
[ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] [ α 1 α 2 ⋮ α n ] = [ γ 1 γ 2 ⋮ γ n ] \left[ \begin{matrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ a_{n1}&a_{n2}&\cdots &a_{nn}\\ \end{matrix} \right] \left[ \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right]= \left[ \begin{matrix} \gamma_1\\ \gamma_2\\ \vdots\\ \gamma_n \end{matrix} \right] ⎣⎢⎢⎢⎡a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡α1α2⋮αn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡γ1γ2⋮γn⎦⎥⎥⎥⎤
什么样的矩阵 B B B可以满足
B [ β 1 β 2 ⋮ β n ] = [ δ 1 δ 2 ⋮ δ n ] B \left[ \begin{matrix} \beta_1\\ \beta_2\\ \vdots\\ \beta_n \end{matrix} \right]= \left[ \begin{matrix} \delta_1\\ \delta_2\\ \vdots\\ \delta_n \end{matrix} \right] B⎣⎢⎢⎢⎡β1β2⋮βn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡δ1δ2⋮δn⎦⎥⎥⎥⎤
B W − 1 [ α 1 α 2 ⋮ α n ] = W − 1 [ γ 1 γ 2 ⋮ γ n ] BW^{-1} \left[ \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right]=W^{-1} \left[ \begin{matrix} \gamma_1\\ \gamma_2\\ \vdots\\ \gamma_n \end{matrix} \right] BW−1⎣⎢⎢⎢⎡α1α2⋮αn⎦⎥⎥⎥⎤=W−1⎣⎢⎢⎢⎡γ1γ2⋮γn⎦⎥⎥⎥⎤
所以矩阵 A , B A,B A,B的关系为
B = W − 1 A W B=W^{-1}AW B=W−1AW
这正是相似矩阵的定义式
特征基和对角化
可对角化的矩阵是相似于对角阵的矩阵
Λ = S − 1 A S \Lambda=S^{-1}AS Λ=S−1AS
如果以基变换的角度来审视对角化
A A A描述了某基下的线性变换,有特征向量矩阵 S S S,也是从现有基过渡到特征基的过渡矩阵。
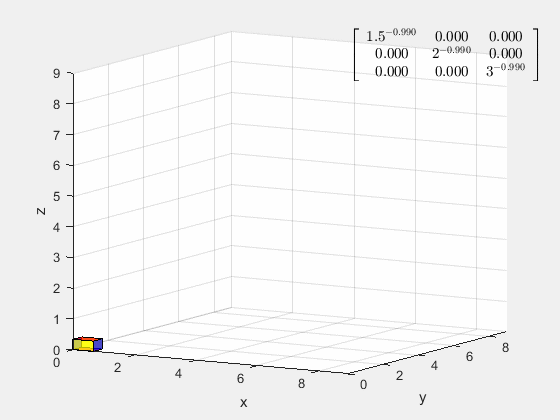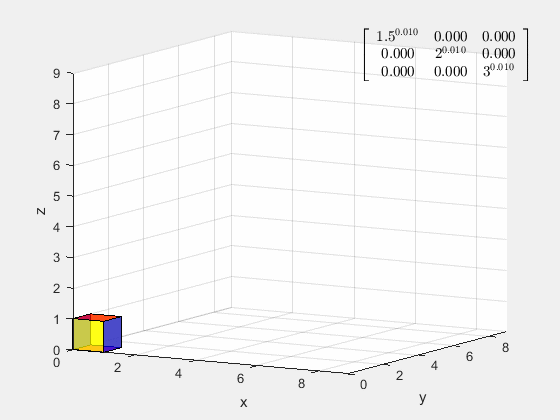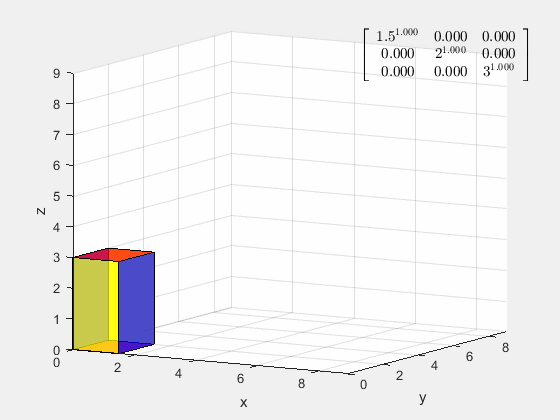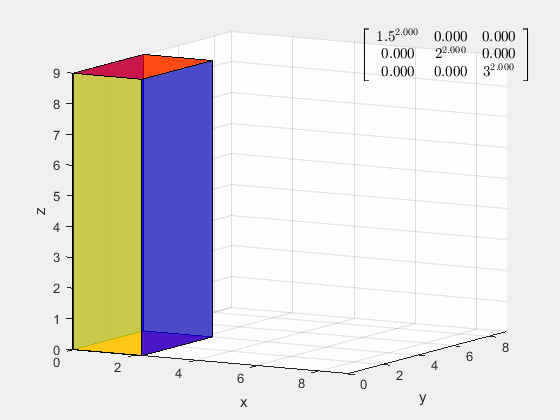
为什么要选取特征基,线性变换在特征基下可以表示成对角阵,其在多次线性变换后基不会偏离原来的方向,各坐标之间不会相互耦合。
[ 1.5 2 3 ] a \left[ \begin{matrix} 1.5&&\\ &2&\\ &&3\\ \end{matrix} \right]^a ⎣⎡1.523⎦⎤a
这篇关于[笔记][总结] MIT线性代数 Gilbert Strang 线性变换和基变换的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






