04 矩阵乘法与线性变换复合

2023-11-05 12:04
文章标签 复合 04 矩阵 乘法 线性变换

本文主要是介绍04 矩阵乘法与线性变换复合，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

矩阵乘法与线性变换复合

  • 复合变换

这是关于3Blue1Brown "线性代数的本质"的学习笔记。

复合变换

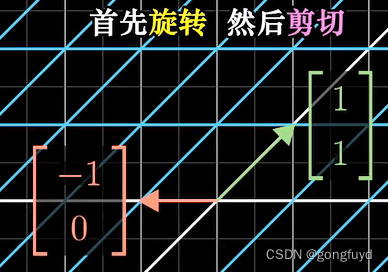
在这里插入图片描述

图1 复合变换
复合变换原则，依次变换，即先变换的矩阵乘待变换的向量后，得到的结果，再用后变换的矩阵乘此结果向量。从矩阵角度描述，即先变换对应的矩阵M1在后变换对应矩阵M2的右侧。

注意：相继两次变换，顺序不同，得到的结果不同。比如，先逆时针旋转90°，再剪贴；与先剪贴，再逆时针旋转90°；这两种方式得到的最终结果不同。
也可以从矩阵相乘看出来这个不同： M 2 M 1 ≠ M 2 M 1 M_2M_1\neq M_2M_1 M2​M1​=M2​M1​

在这里插入图片描述
在这里插入图片描述

这篇关于04 矩阵乘法与线性变换复合的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/349738。

相关文章

hdu 4565 推倒公式+矩阵快速幂

hdu 4565 推倒公式+矩阵快速幂

题意 求下式的值： Sn=⌈ (a+b√)n⌉%m S_n = \lceil\ (a + \sqrt{b}) ^ n \rceil\% m 其中： 0<a,m<215 0< a, m < 2^{15} 0<b,n<231 0 < b, n < 2^{31} (a−1)2<b<a2 (a-1)^2< b < a^2 解析 令： An=(a+b√)n A_n = (a +
阅读更多...
hdu 6198 dfs枚举找规律+矩阵乘法

hdu 6198 dfs枚举找规律+矩阵乘法

number number number Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Problem Description We define a sequence  F : ⋅   F0=0,F1=1 ; ⋅   Fn=Fn
阅读更多...
取得 Git 仓库 —— Git 学习笔记 04

取得 Git 仓库 —— Git 学习笔记 04

取得 Git 仓库 —— Git 学习笔记 04 我认为， Git 的学习分为两大块：一是工作区、索引、本地版本库之间的交互；二是本地版本库和远程版本库之间的交互。第一块是基础，第二块是难点。 下面，我们就围绕着第一部分内容来学习，先不考虑远程仓库，只考虑本地仓库。 怎样取得项目的 Git 仓库？ 有两种取得 Git 项目仓库的方法。第一种是在本地创建一个新的仓库，第二种是把其他地方的某个
阅读更多...
浙大数据结构：04-树7 二叉搜索树的操作集

浙大数据结构：04-树7 二叉搜索树的操作集

这道题答案都在PPT上，所以先学会再写的话并不难。 1、BinTree Insert( BinTree BST, ElementType X ) 递归实现，小就进左子树，大就进右子树。 为空就新建结点插入。 BinTree Insert( BinTree BST, ElementType X ){if(!BST){BST=(BinTree)malloc(sizeof(struct TNo
阅读更多...
读软件设计的要素04概念的关系

读软件设计的要素04概念的关系

1. 概念的关系 1.1. 概念是独立的，彼此间无须相互依赖 1.1.1. 一个概念是应该独立地被理解、设计和实现的 1.1.2. 独立性是概念的简单性和可重用性的关键 1.2. 软件存在依赖性 1.2.1. 不是说一个概念需要依赖另一个概念才能正确运行 1.2.2. 只有当一个概念存在时，包含另一个概念才有意义 1.3. 概念依赖关系图简要概括了软件的概念和概念存在的理
阅读更多...
线性代数|机器学习-P35距离矩阵和普鲁克问题

线性代数|机器学习-P35距离矩阵和普鲁克问题

文章目录 1. 距离矩阵2. 正交普鲁克问题3. 实例说明 1. 距离矩阵 假设有三个点 x 1 , x 2 , x 3 x_1,x_2,x_3 x1​,x2​,x3​,三个点距离如下： ∣ ∣ x 1 − x 2 ∣ ∣ 2 = 1 , ∣ ∣ x 2 − x 3 ∣ ∣ 2 = 1 , ∣ ∣ x 1 − x 3 ∣ ∣ 2 = 6 \begin{equation} ||x
阅读更多...
【线性代数】正定矩阵，二次型函数

【线性代数】正定矩阵，二次型函数

本文主要介绍正定矩阵，二次型函数，及其相关的解析证明过程和各个过程的可视化几何解释（深蓝色字体）。 非常喜欢清华大学张颢老师说过的一段话：如果你不能用可视化的方式看到事情的结果，那么你就很难对这个事情有认知，认知就是直觉，解析的东西可以让你理解，但未必能让你形成直觉，因为他太反直觉了。 正定矩阵 定义 给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 ，有 恒成
阅读更多...
[苍穹外卖]-04菜品管理接口开发

[苍穹外卖]-04菜品管理接口开发

效果预览 新增菜品 需求分析 查看产品原型分析需求, 包括用到哪些接口, 业务的限制规则 业务规则 菜品名称必须是唯一的菜品必须属于某个分类下, 不能单独存在新增菜品时可以根据情况选择菜品的口味每个菜品必须对应一张图片 接口设计 根据类型查询分类接口 文件上传接口 新增菜品接口 数据表设计 设计dish菜品表 和 dish_fl
阅读更多...
python科学计算：NumPy 线性代数与矩阵操作

python科学计算：NumPy 线性代数与矩阵操作

1 NumPy 中的矩阵与数组 在 NumPy 中，矩阵实际上是一种特殊的二维数组，因此几乎所有数组的操作都可以应用到矩阵上。不过，矩阵运算与一般的数组运算存在一定的区别，尤其是在点积、乘法等操作中。 1.1 创建矩阵 矩阵可以通过 NumPy 的 array() 函数创建。矩阵的形状可以通过 shape 属性来访问。 import numpy as np# 创建一个 2x3 矩阵mat
阅读更多...
【动手学深度学习】04 数据操作 + 数据预处理（个人向笔记）

【动手学深度学习】04 数据操作 + 数据预处理（个人向笔记）

数据操作 N维数组是机器学习和神经网络的主要数据结构其中 2-d 矩阵中每一行表示每一行表示一个样本 当维度来到三维的时候则可以表示成一张图片，再加一维就可以变成多张图片，再加一维则可以变成一个视频 访问元素 冒号表示从冒号左边的元素到冒号右边的前一个元素（开区间），其中如果左边为空，那么表示从第一个开始，如果右边为空，那么表示访问到最后一个，如果两边都为空，则表示全部访问其中一行中我们指
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2