本文主要是介绍【线性代数的本质 - 系列合集】04 矩阵乘法与线性变换复合的联系(万字详文),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
兄弟们,没看过视频的先滚去看视频!!!笔记是用来复习的
课程是blibli和youtube上的:
线性代数的本质 - 系列合集
Linear transformations and matrices | Chapter 3, Essence of linear algebra
嘿 大家好!

上期视频结束前
我展示了线性变换长什么样,以及如何用矩阵描述它们
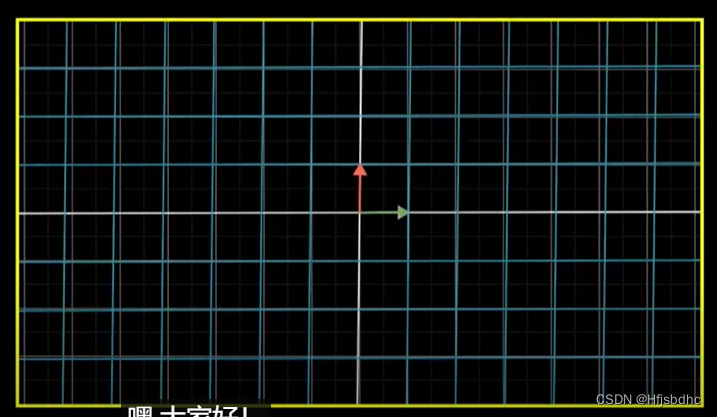
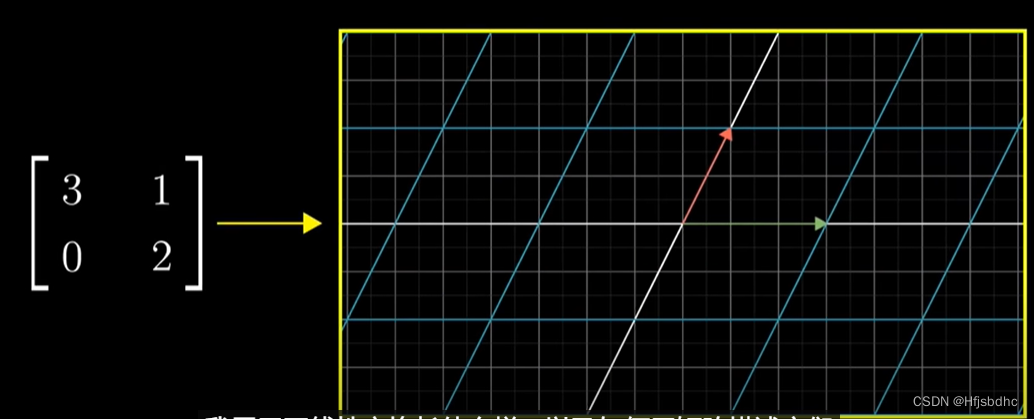
这值得我们快速回顾一下,因为它们实在是很重要
当然,如果你觉得不是“回顾”这么简单,那就再回去看看上期视频吧

严格意义上说,线性变换是将向量作为输入和输出的一类函数

但是上期视频中,我说过可以将线性变换看作对空间的挤压伸展
它保持网格线平行且等距分布,并且保持原点不变

关键的一点在于,线性变换由它对空间的基向量的作用完全决定
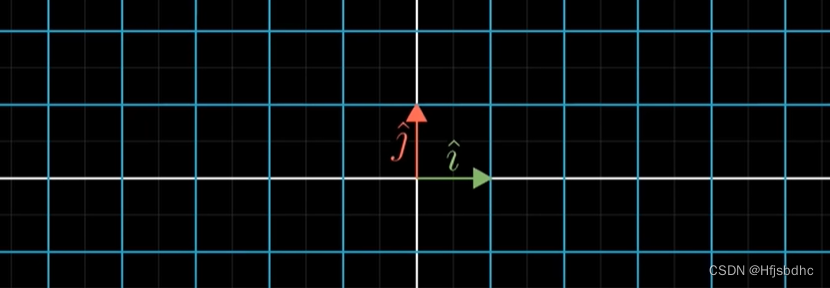
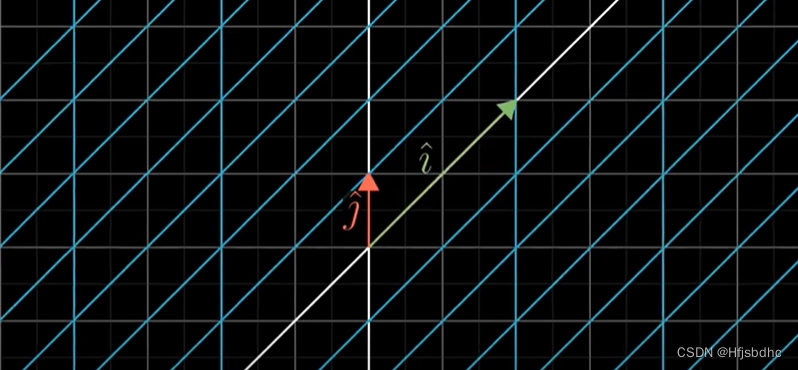
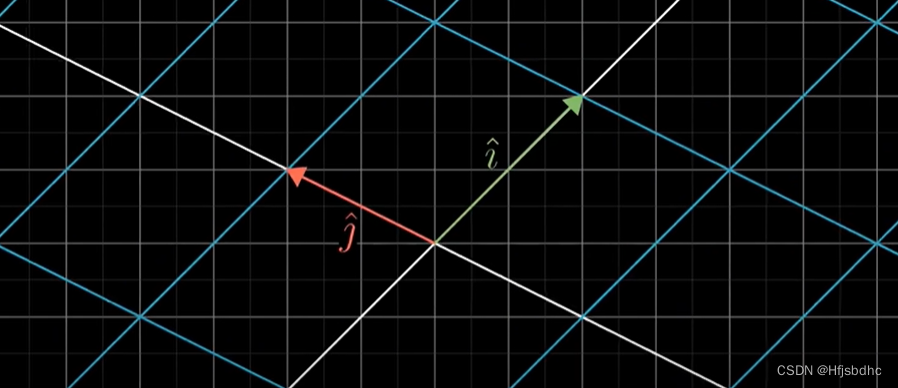
在二维空间中,基向量就是i帽和j帽
这是因为其他任意向量都能表示为基向量的线性组合
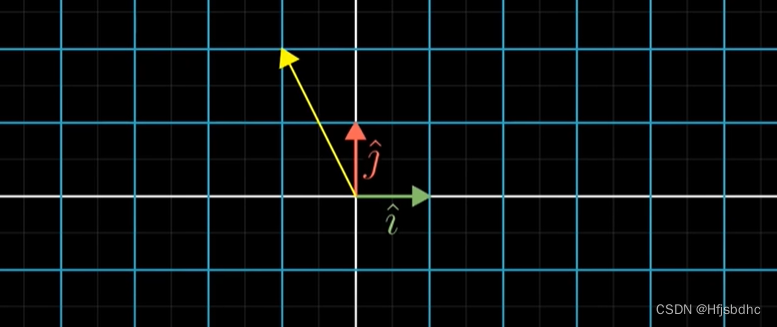
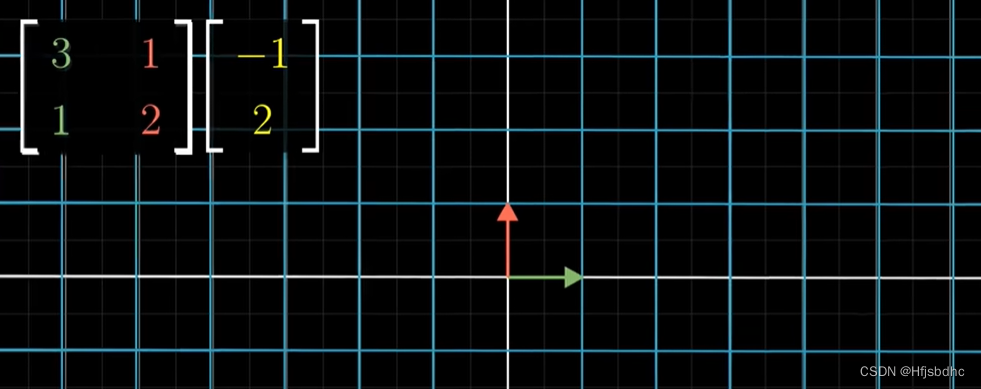
坐标为(x, y)的向量就是x乘以i帽加上y乘以j帽
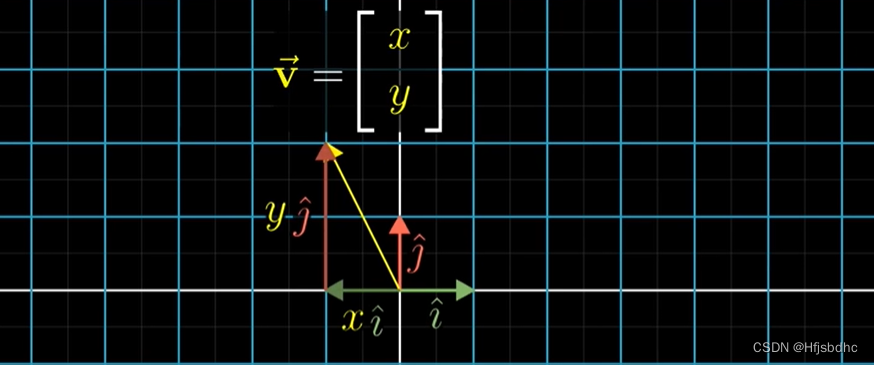
在线性变换之后
网格线保持平行且等距分布这一性质有个绝妙的推论
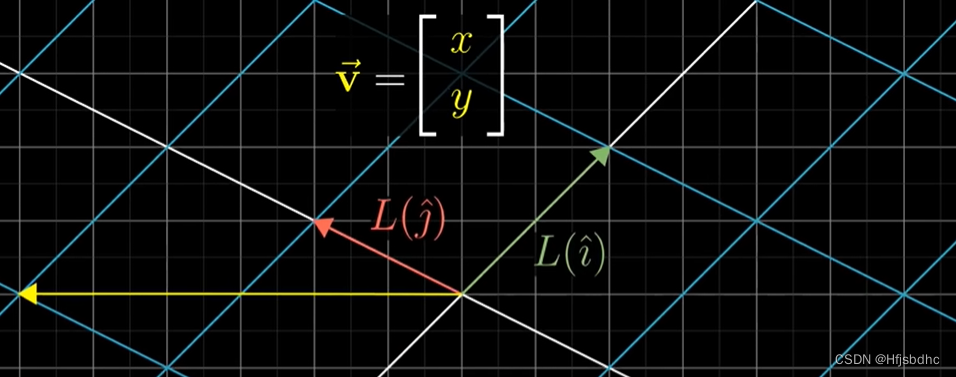
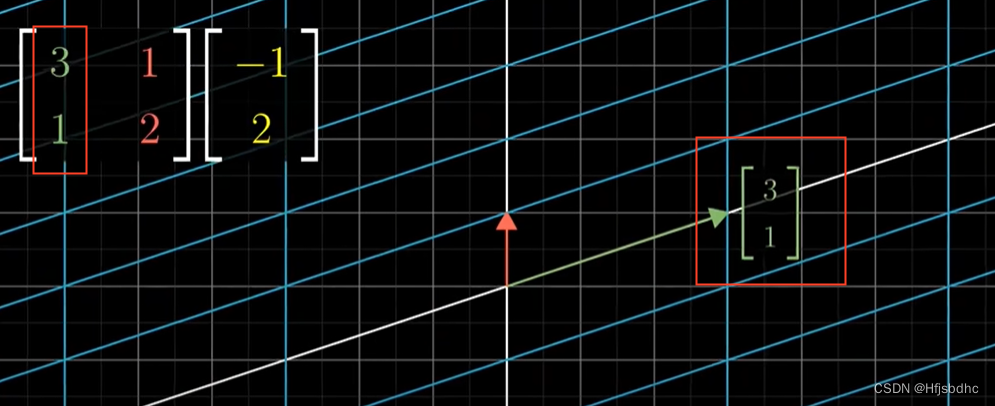
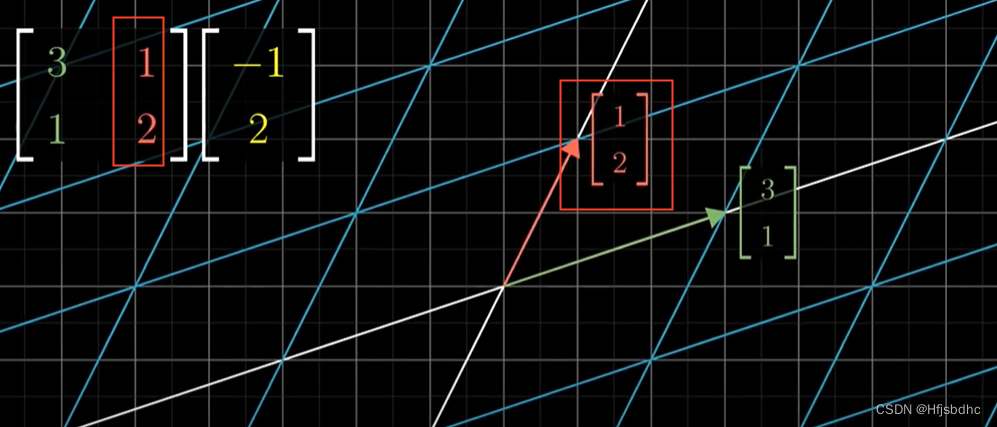
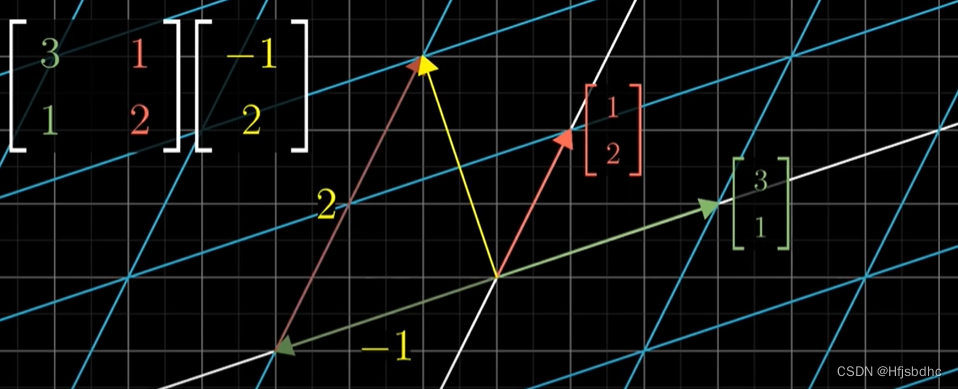
向量(x, y)变换之后的结果,将是x乘以变换后的i帽,加上y乘以变换后的j帽
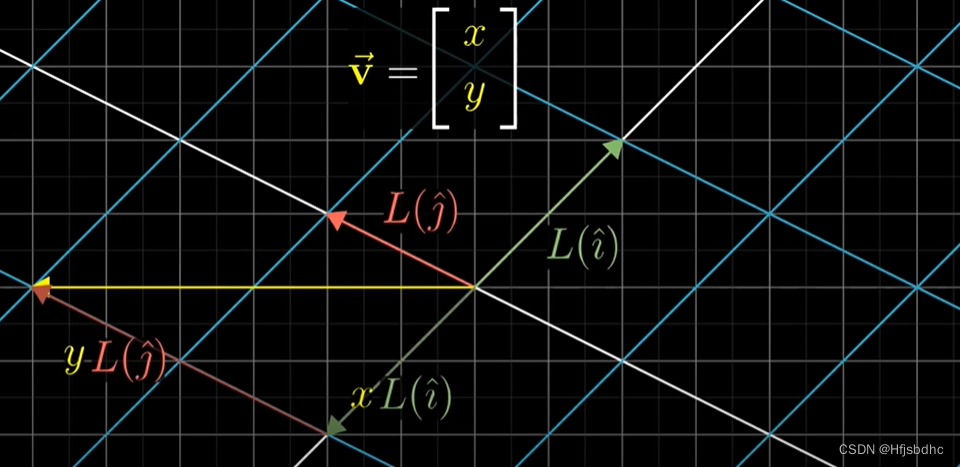
这意味着只要记录下i帽和j帽变换后的位置
你就能计算出一个坐标为(x, y)的向量变换后的坐标
就是x乘以变换后i帽的坐标,加上y乘以变换后j帽的坐标
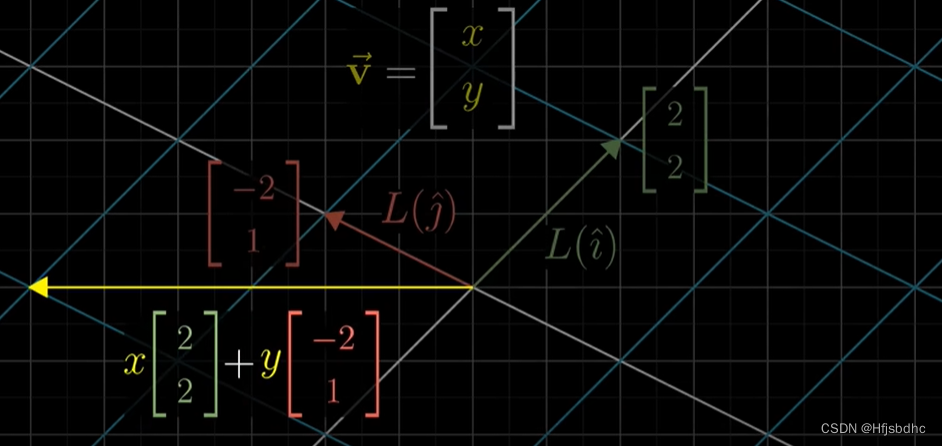
习惯上,我们将变换后i帽和j帽的坐标作为一个矩阵的列
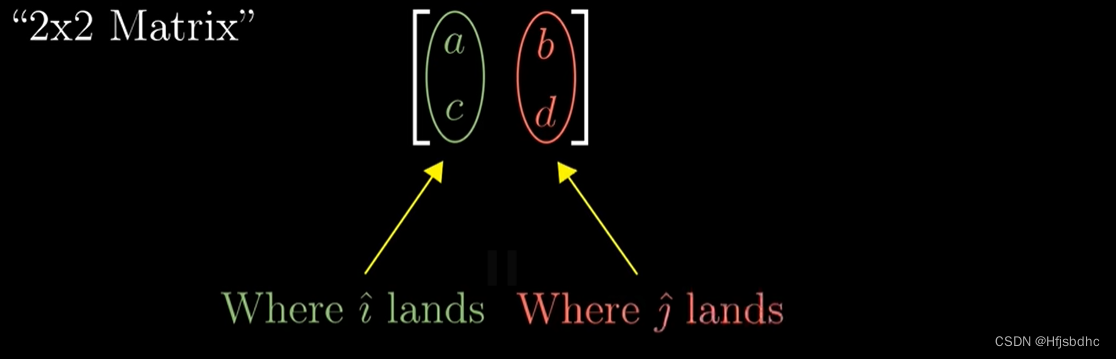
并且将两列分别与x和y相乘后加和的结果定义为矩阵向量乘积
这样,矩阵代表一个特定的线性变换
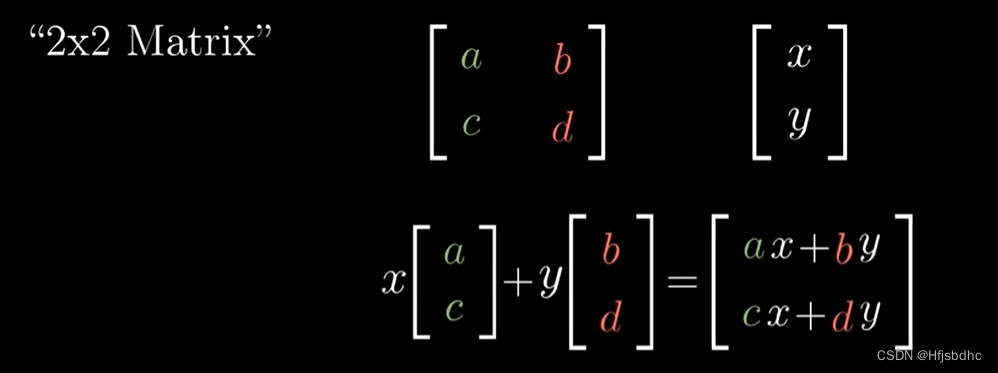

而矩阵与向量相乘
就是将线性变换作用于那个向量
回顾结束!开始新的内容

很多时候你发现你想描述这样一种作用:一个变换之后再进行另一个变换
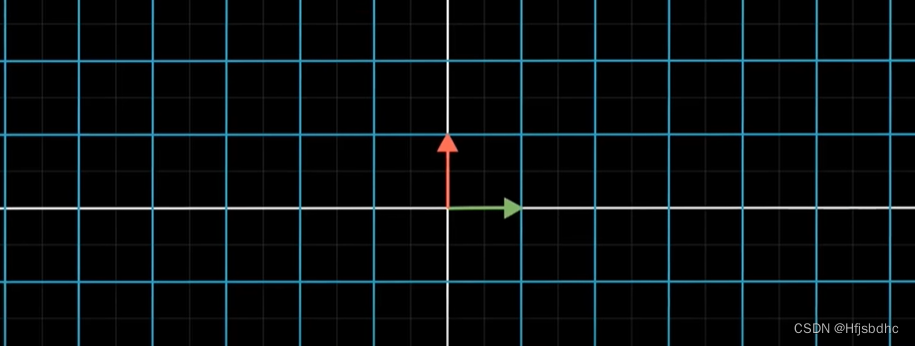
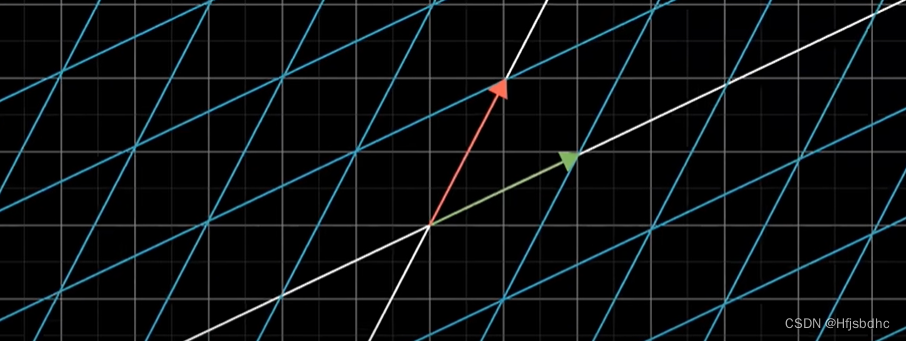
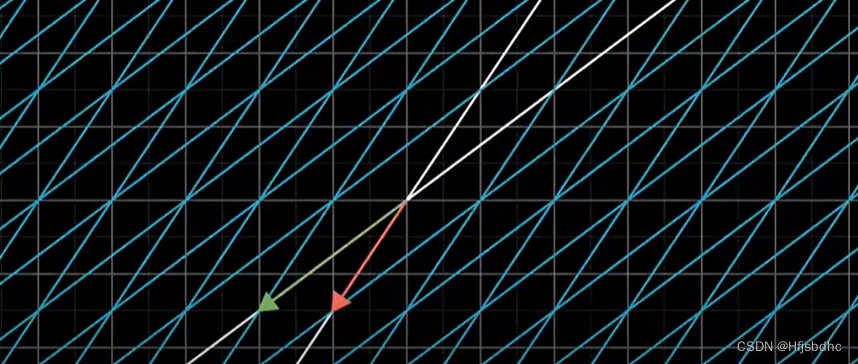
比如说,你想描述
将整个平面逆时针旋转90度后,再进行一次剪切变换会发生什么

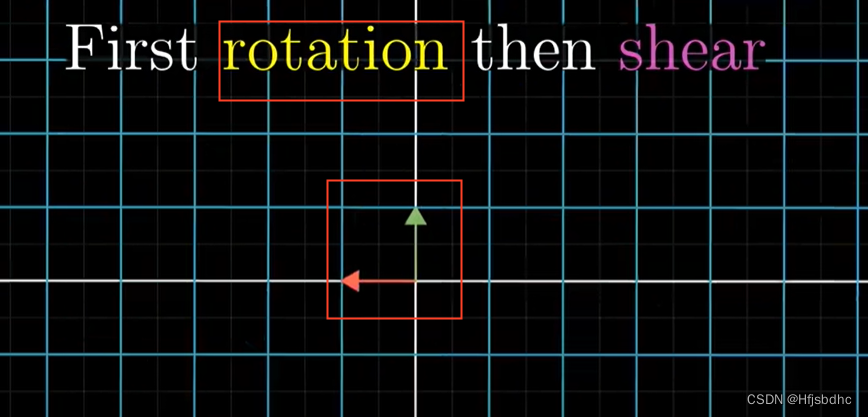
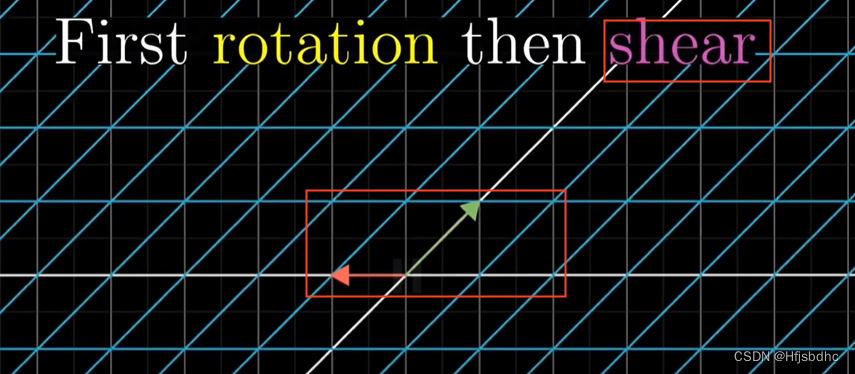
从头到尾的总体作用是另一个线性变换
它与旋转和剪切明显不同
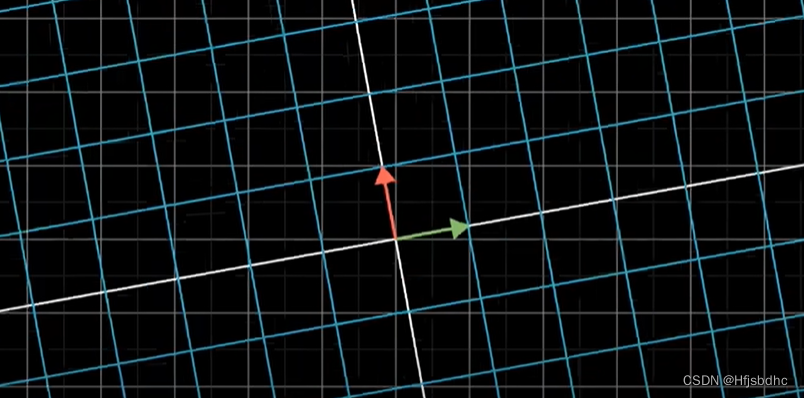
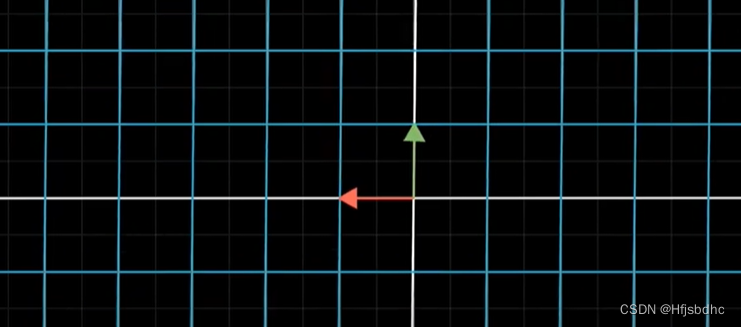
这个新的线性变换通常被称为前两个独立变换的“复合变换”
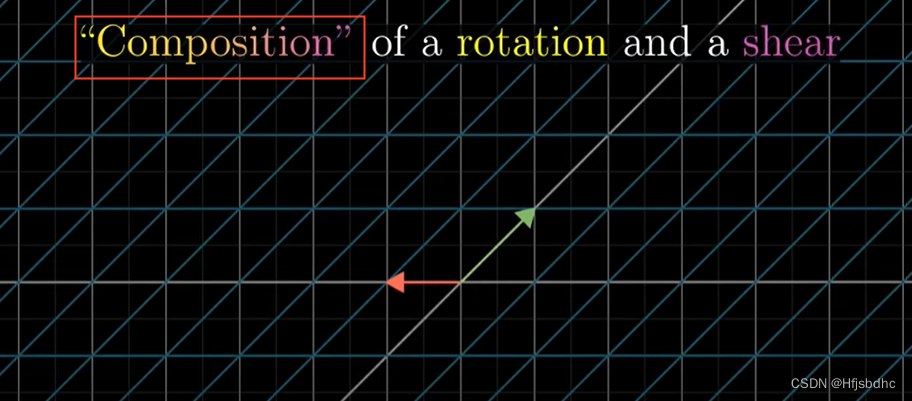
和其他线性变换一样
我们也能通过追踪i帽和j帽,并用矩阵完全描述这个复合变换
在这个例子中,i帽在两个线性变换之后的最终落点是(1, 1)
我们将它作为矩阵的第一列
类似地,j帽最终落在(-1, 0)
我们将它作为矩阵的第二列

这一新的矩阵捕捉到了旋转然后剪切的总体效应
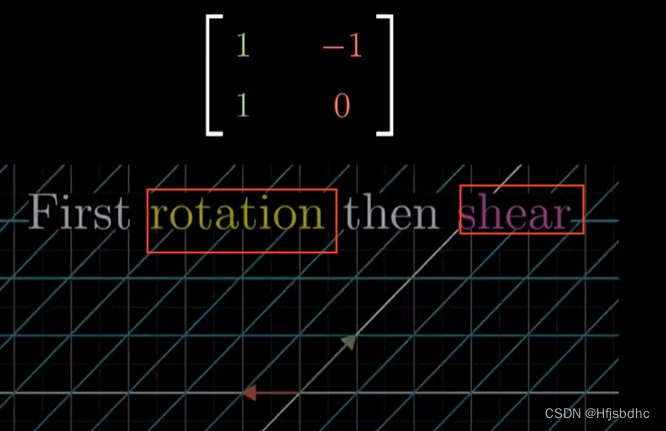
但它是一个单独的作用,而不是两个相继作用的合成
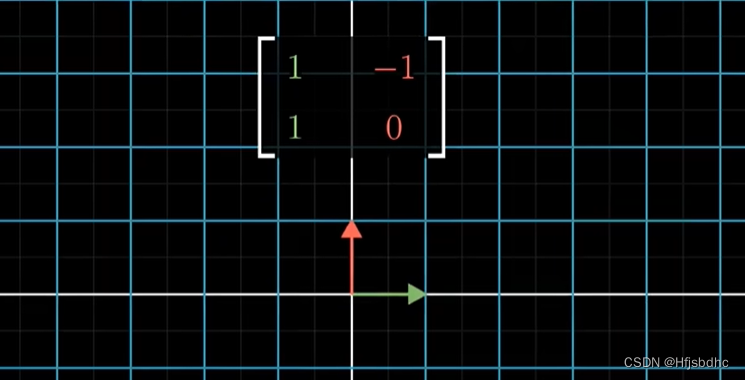
上图通过一次变换直接变成下图,不是两次
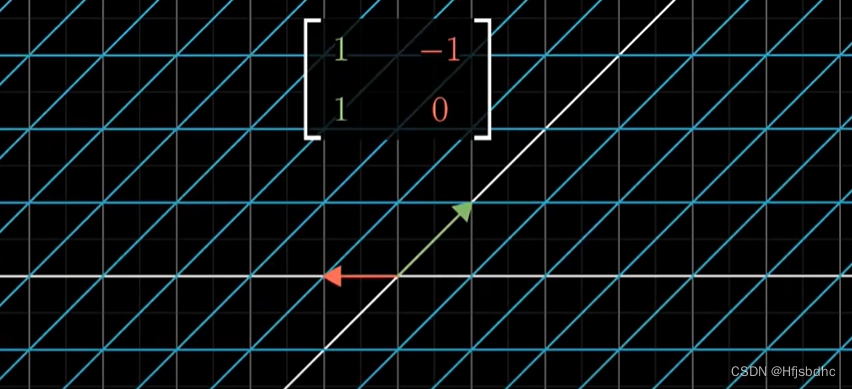
这里有种方法来考虑这个新矩阵
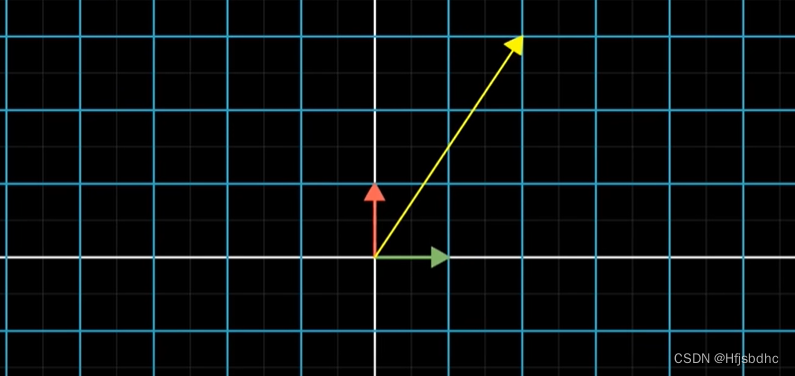
如果你有一个向量,将它进行旋转然后剪切
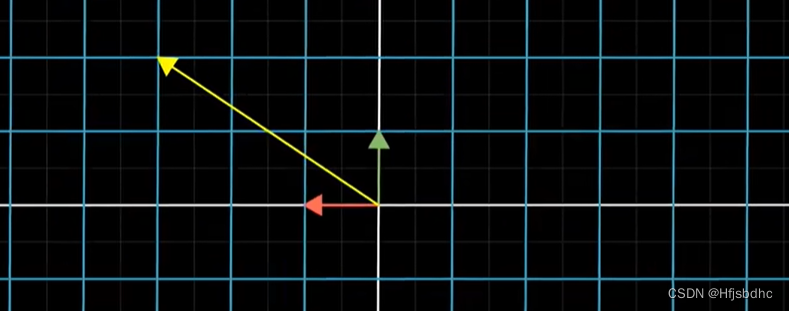
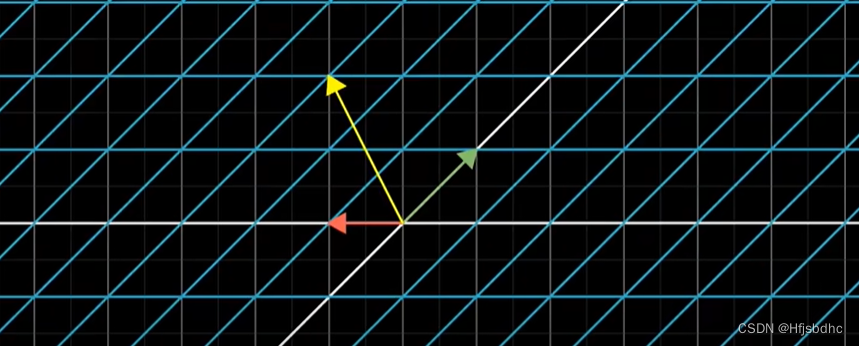
一个麻烦的计算方法是:
首先将它左乘旋转矩阵
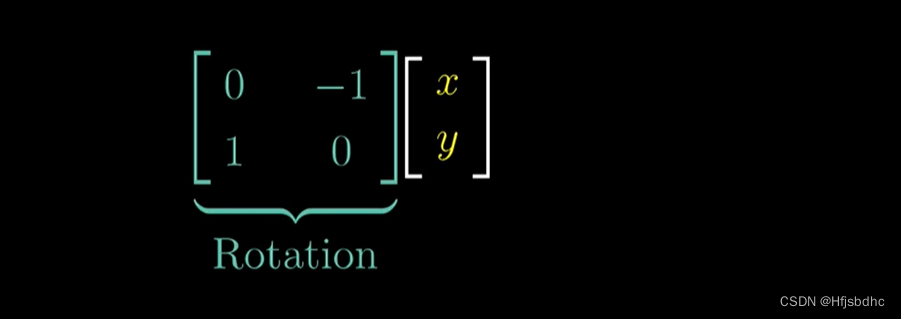
然后将得到的结果再左乘剪切矩阵
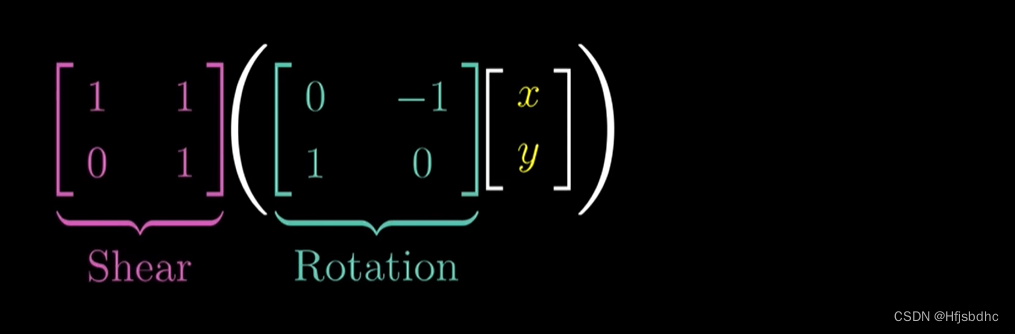
从数值角度看,这意味着对一个给定向量进行旋转然后剪切
但是无论所选向量是什么,结果都应该与复合变换作用的结果完全相同
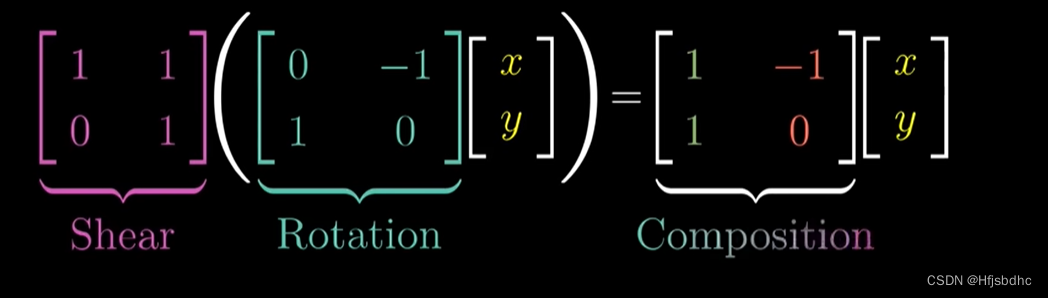
因为新矩阵应当捕捉到了旋转然后剪切的相同总体效应
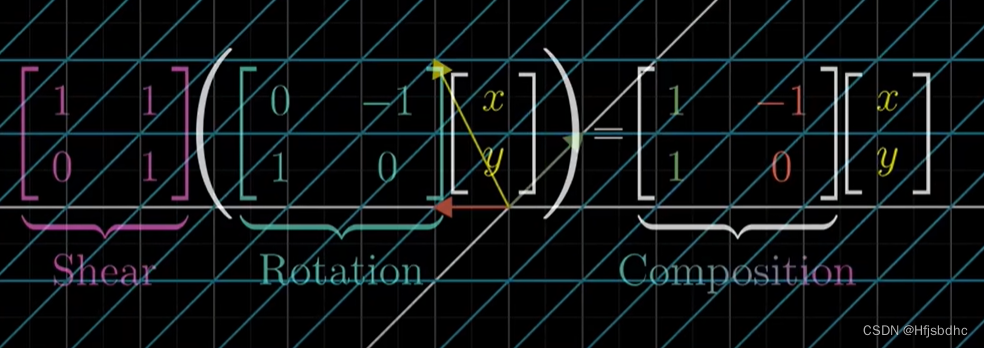
根据我们这里所写下的内容
我认为将这个新矩阵称为最初两个矩阵的积是合理的,不是吗?
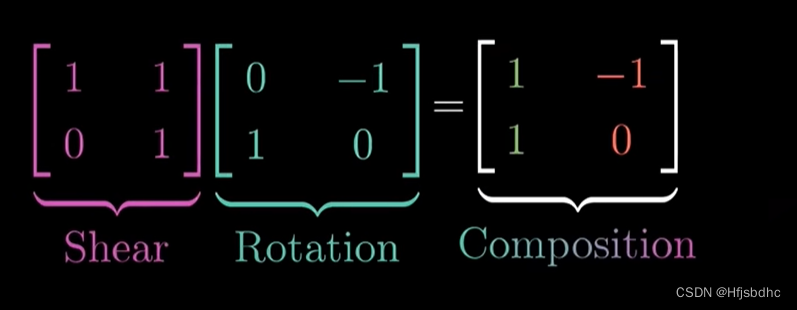
我们很快就能搞清楚如何在更普遍的情况下计算这个乘积
但是这样太容易迷失在数字丛林当中
时刻记得
两个矩阵相乘有着几何意义,也就是两个线性变换相继作用
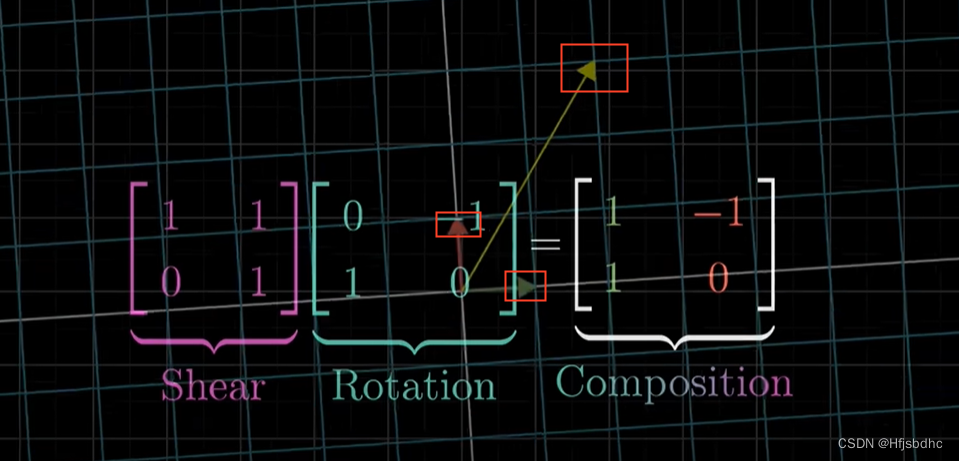
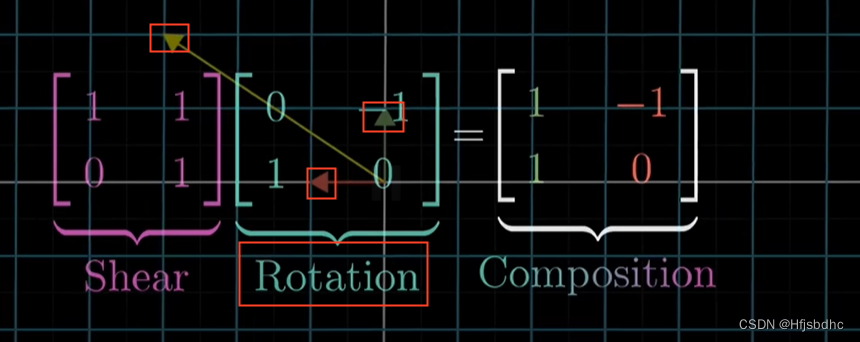
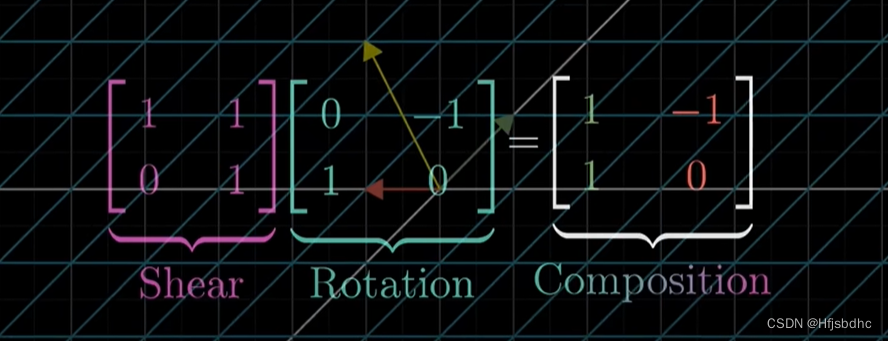
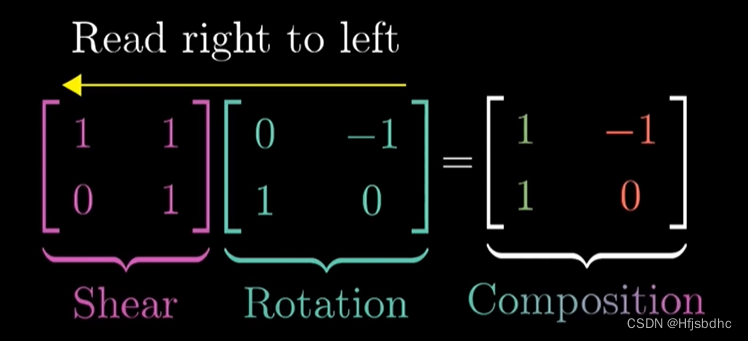
这里有件奇怪的事,就是这个乘积需要从右向左读
首先应用右侧矩阵所描述的变换
然后再应用左侧矩阵所描述的变换
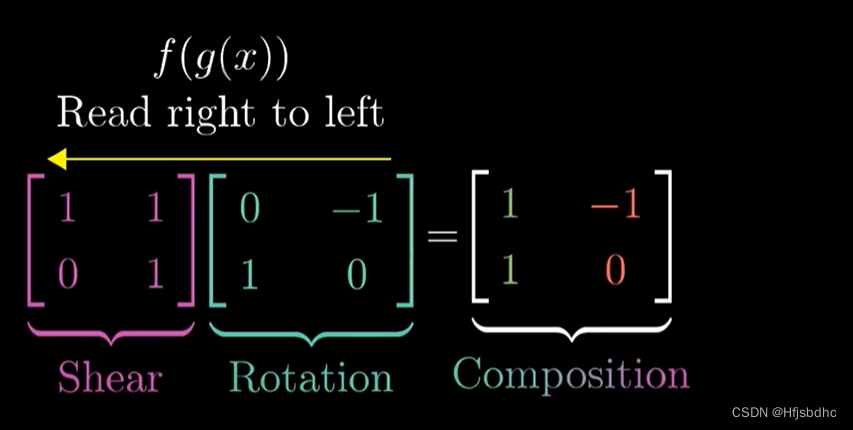
它起源于函数的记号,因为我们将函数写在变量左侧
所以每次将两个函数复合时,你总是要从右向左读
对希伯来读者是好消息,对其他人则是坏消息
我们再看一个例子
一个矩阵,两列为(1, 1)和(-2, 0)
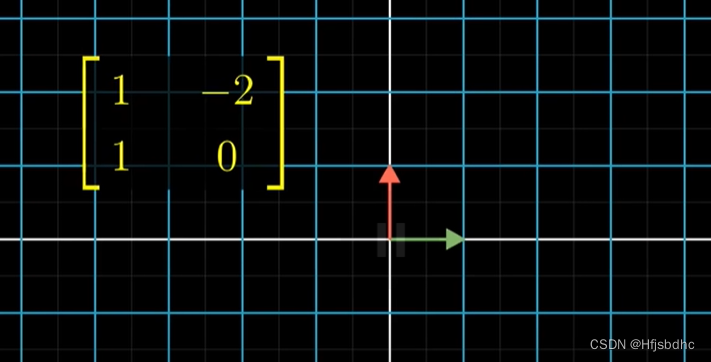
它所代表的变换长这样
我们称它为M1
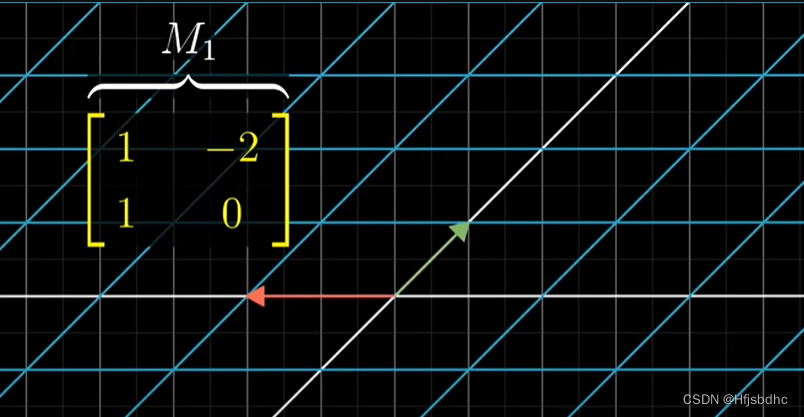
另一个矩阵,两列为(0, 1)和(2, 0)
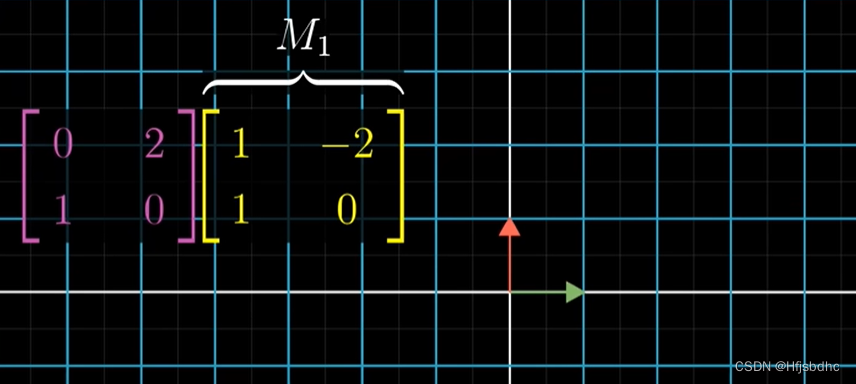
它所代表的变换长这样
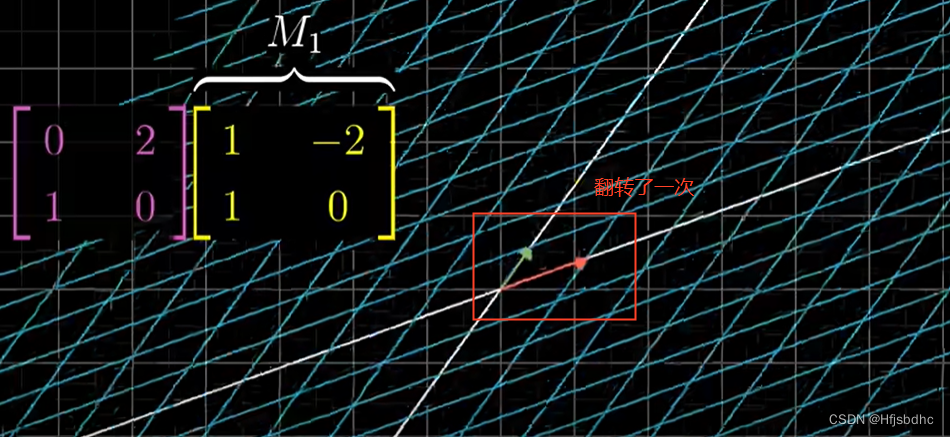
我们称它为M2
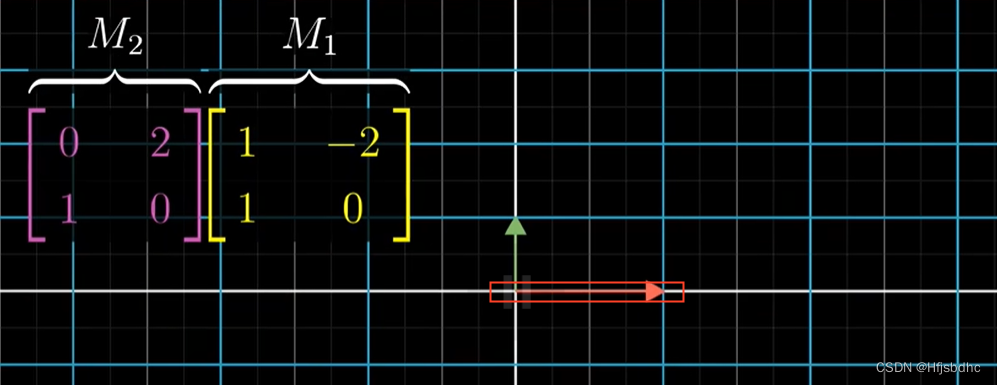
M1和M2先后作用,总体效果是一个新的变换,我们来求解它的矩阵
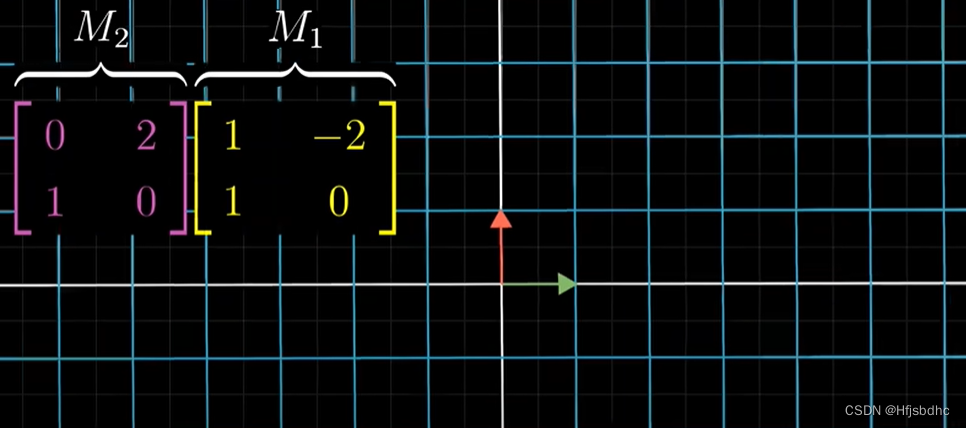
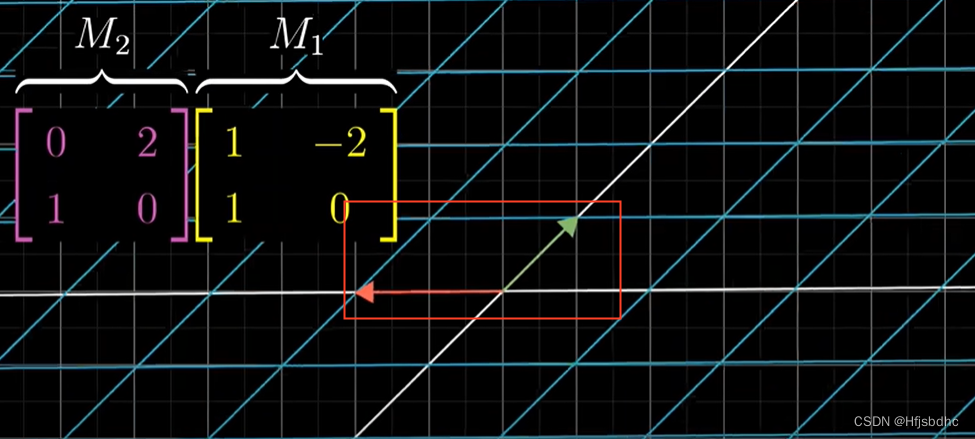
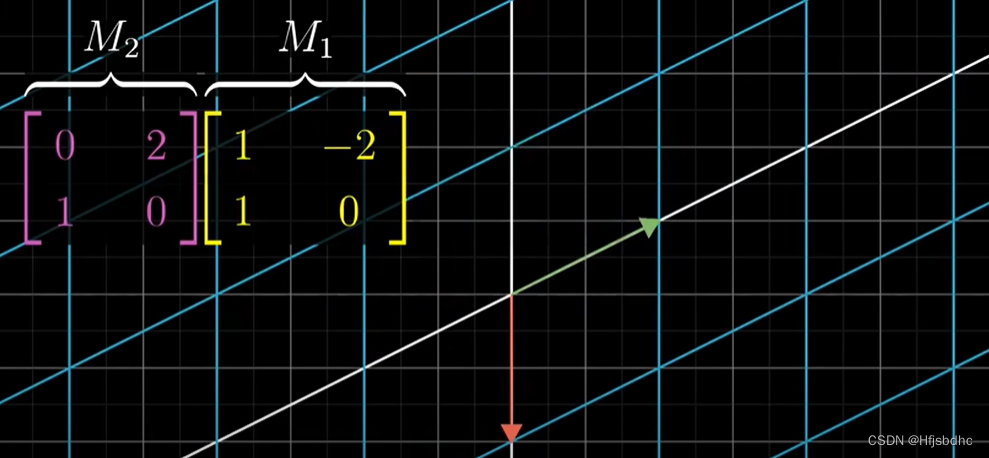
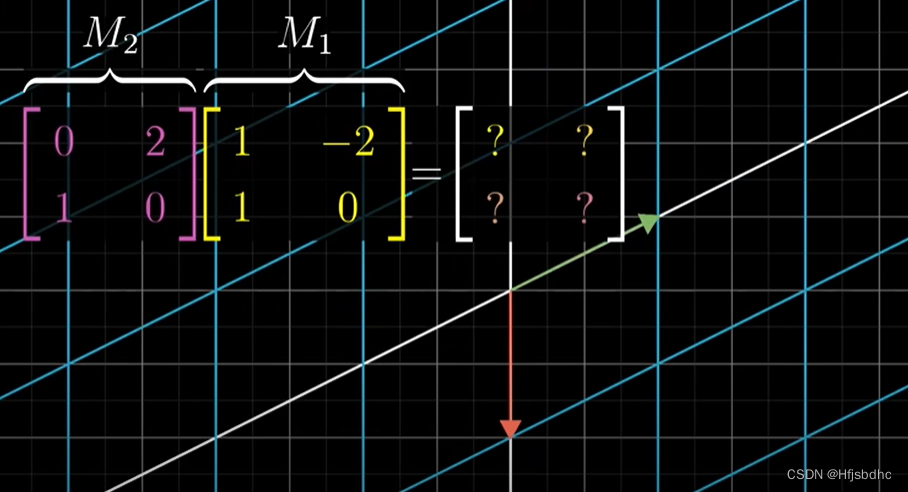
但是这一次,我们来尝试一下不通过观看动画
只使用每个矩阵的数值来求解
首先,我们得算出i帽的去向
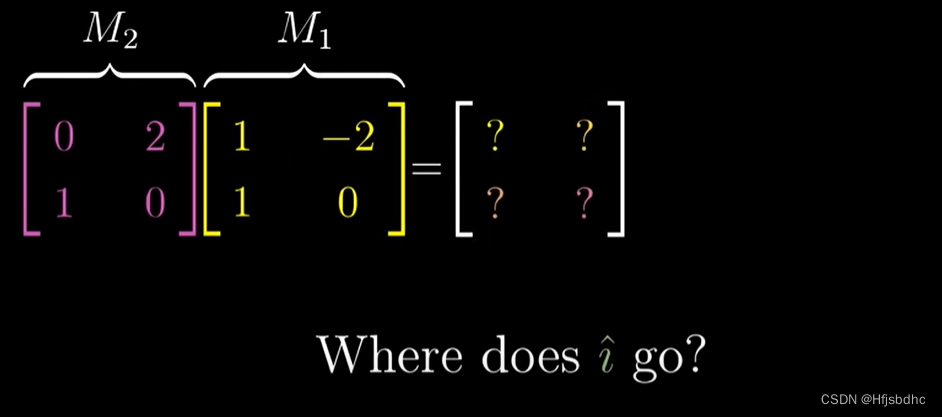
在M1作用之后
按照定义,i帽的新坐标由M1的第一列给出,也就是(1, 1)
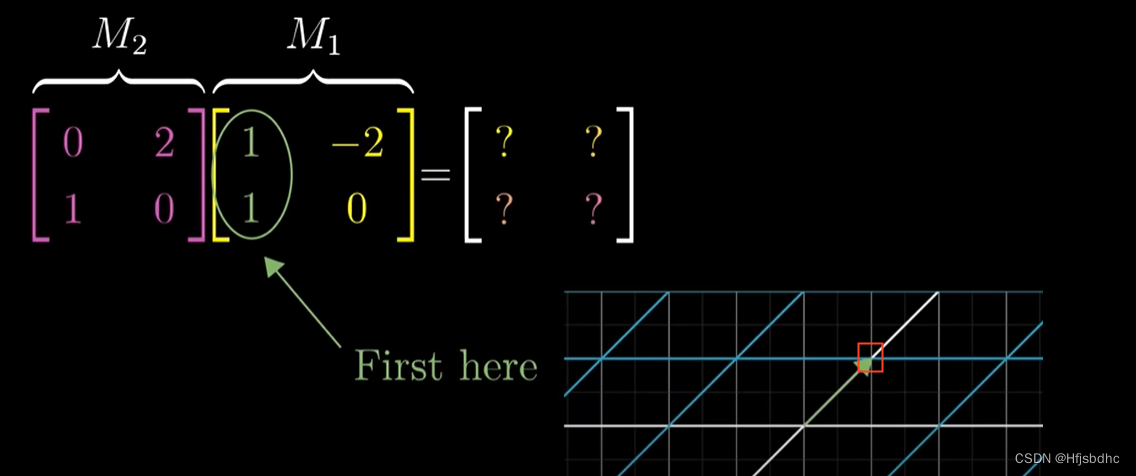
要看看M2作用之后会发生什么,将矩阵M2乘以向量(1, 1)
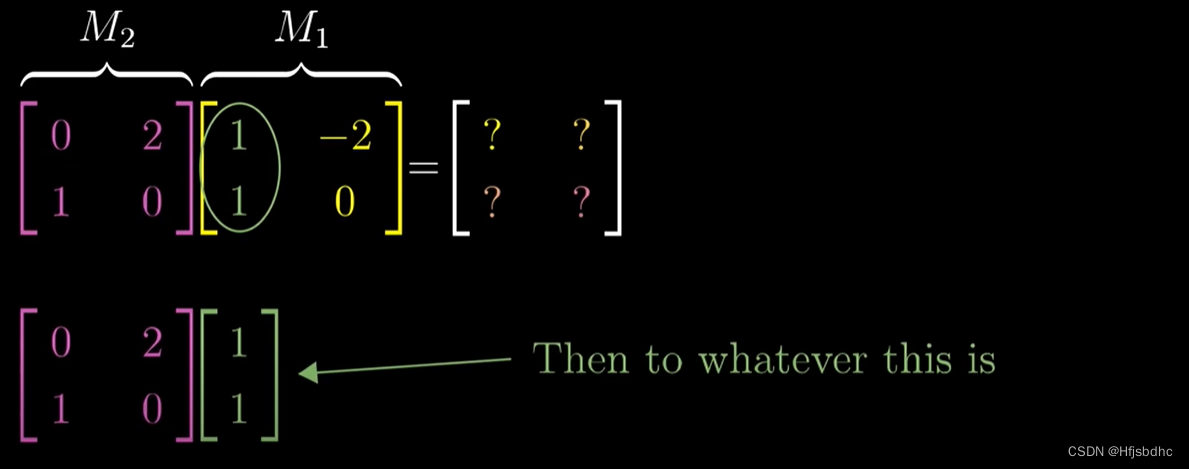

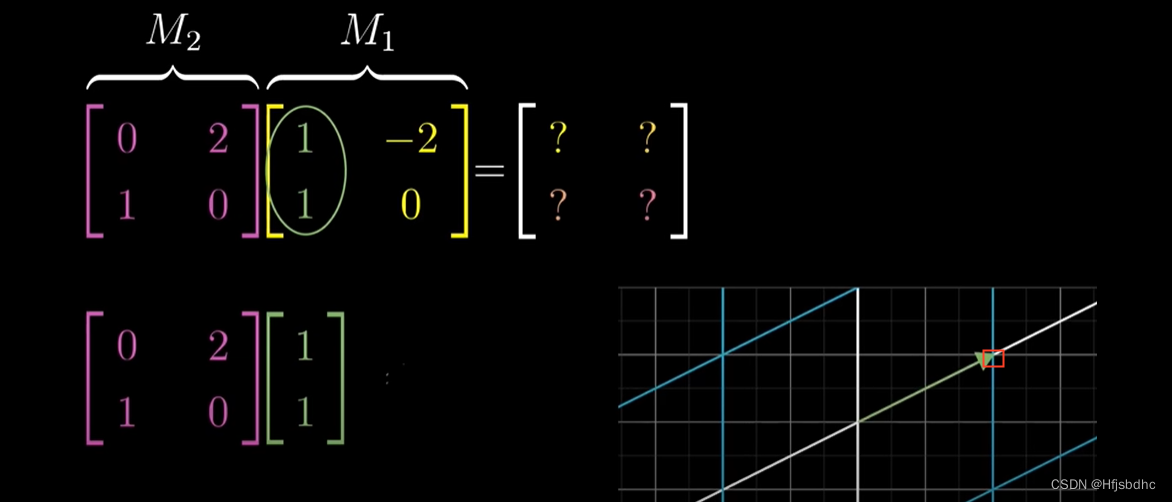
用上期视频中我讲述的方法计算出结果,你会得到向量(2, 1)
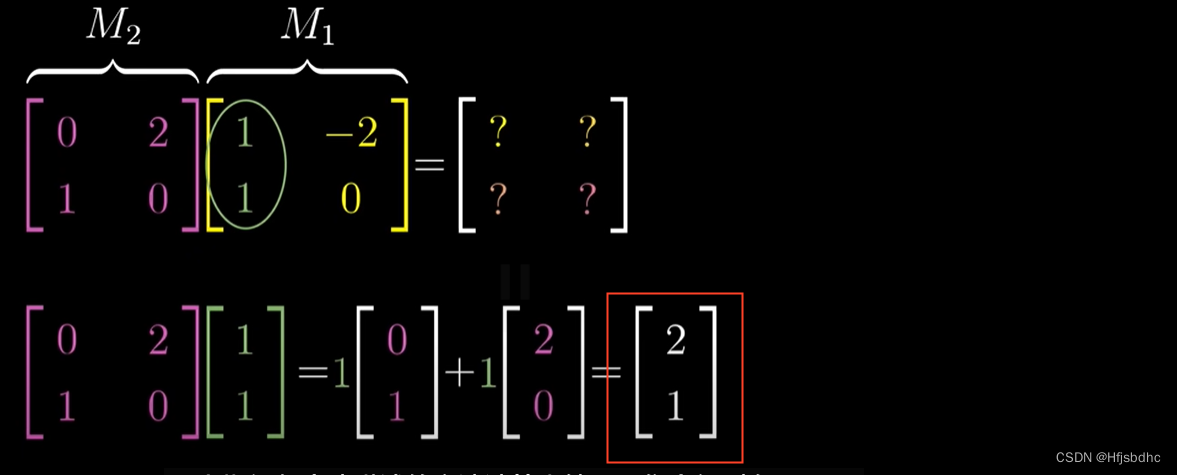
这就是复合矩阵的第一列
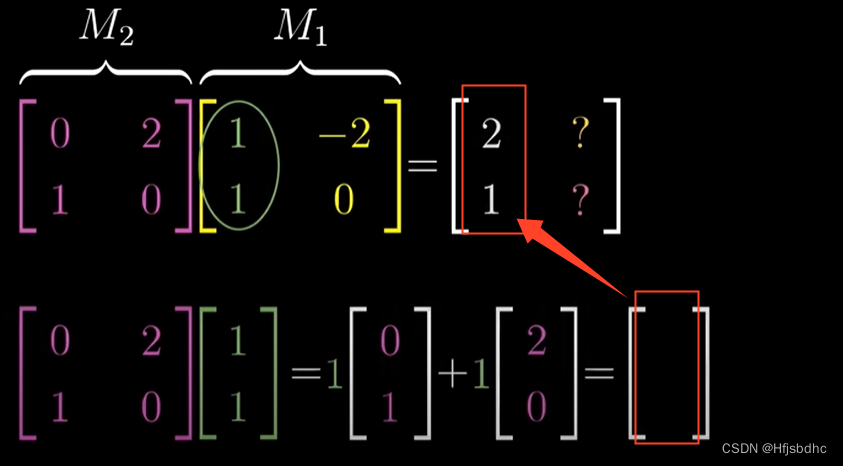
类似地,M1的第二列告诉我们j帽首先落在(-2, 0)
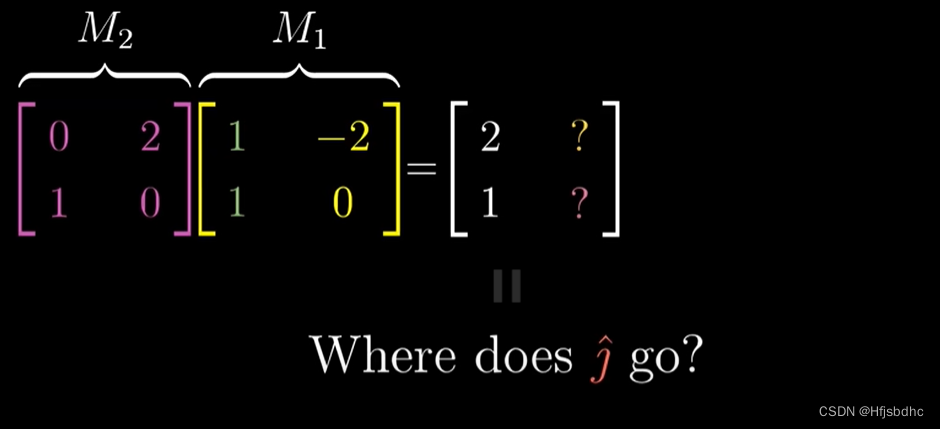
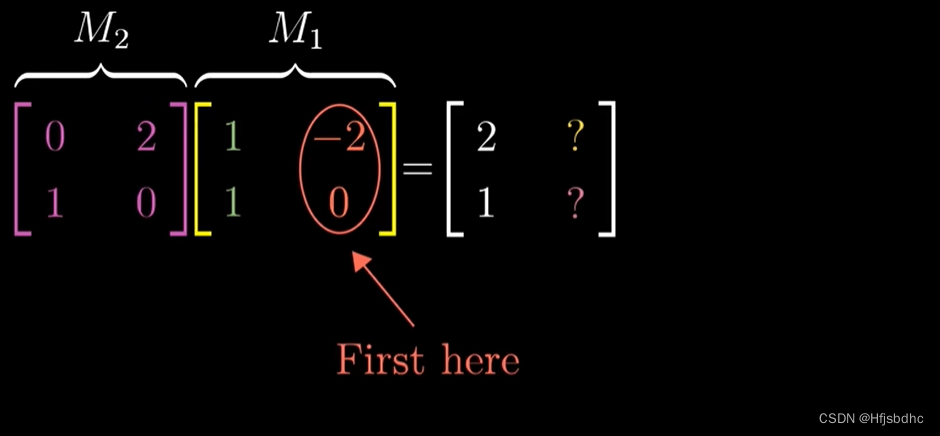
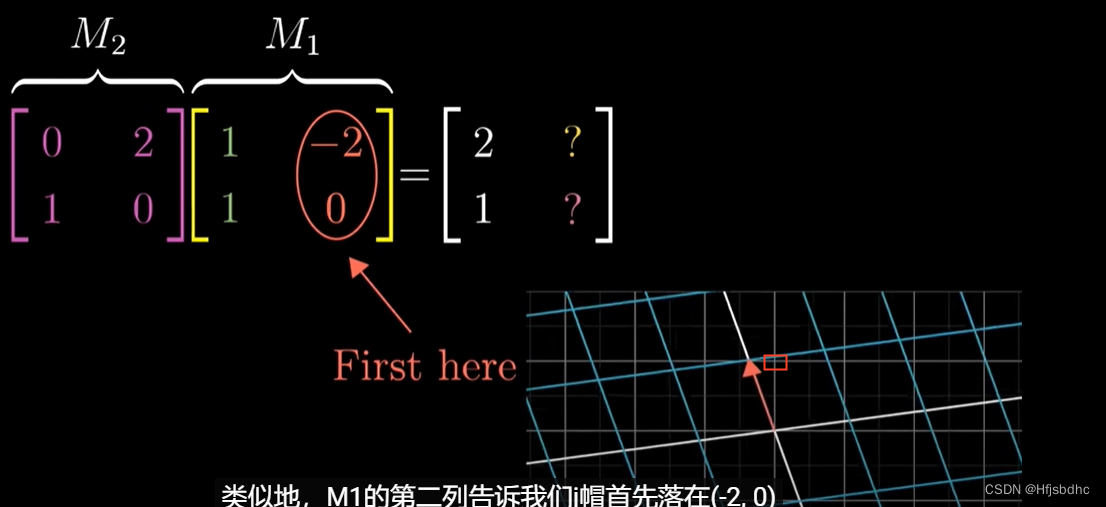
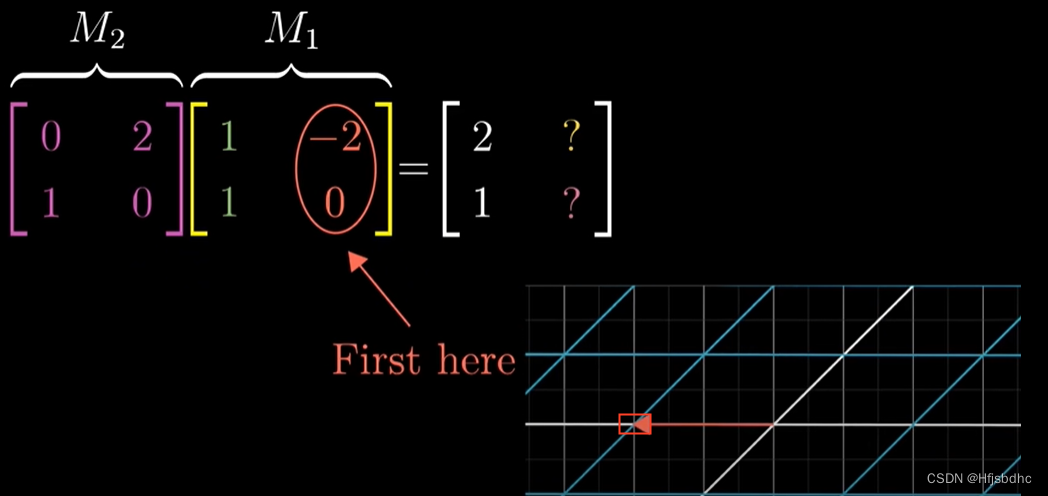
然后将M2作用于这个向量
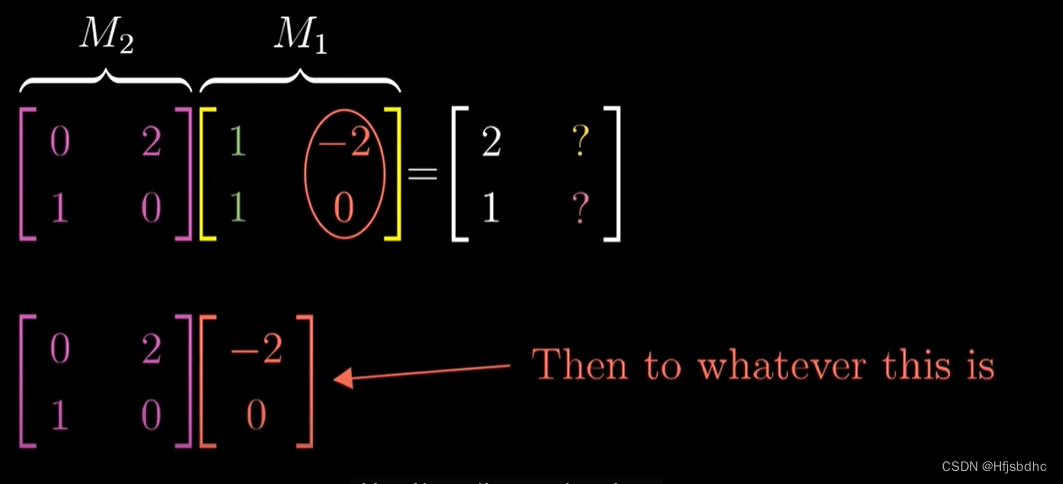
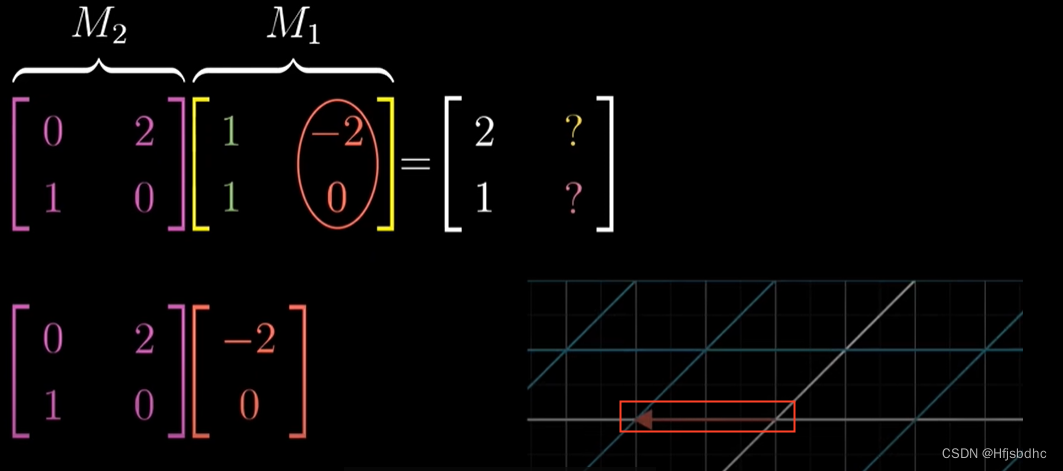
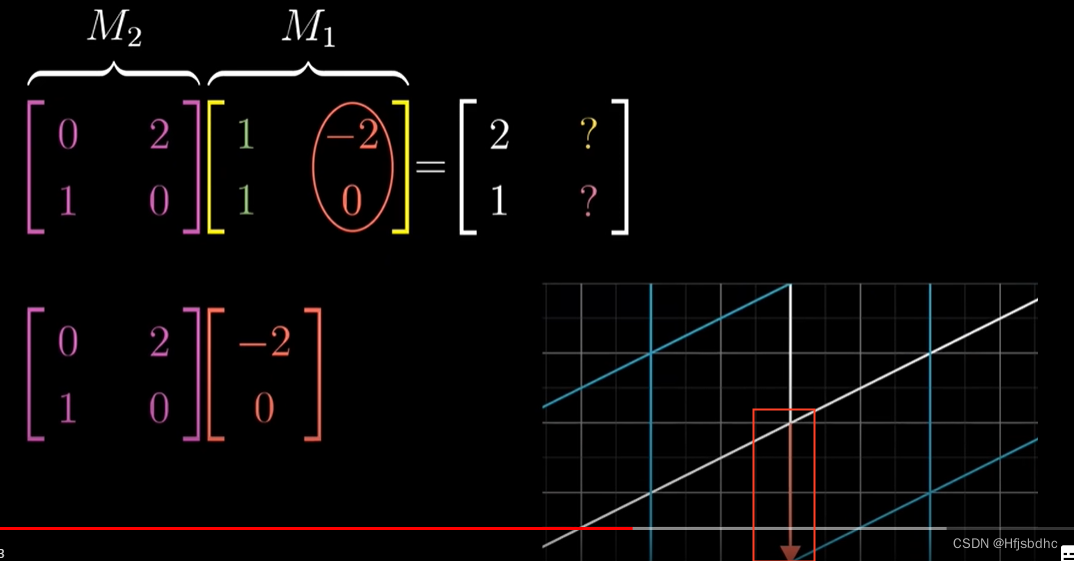
你能根据矩阵向量乘法计算得到(0, -2)
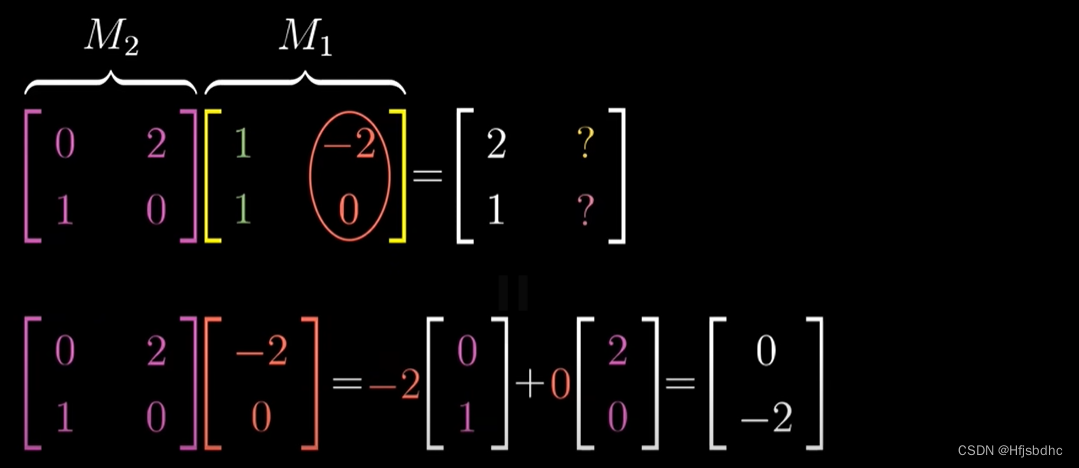
这就是复合矩阵的第二列
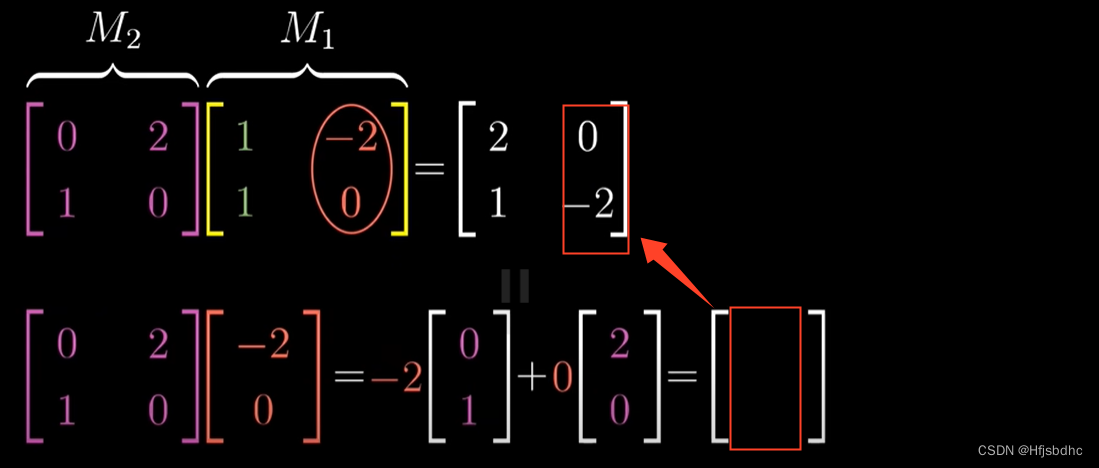
我再重复一次同样的过程,不过这次我们用变量代替数值
只是为了说明这一推理过程对于任意矩阵都适用
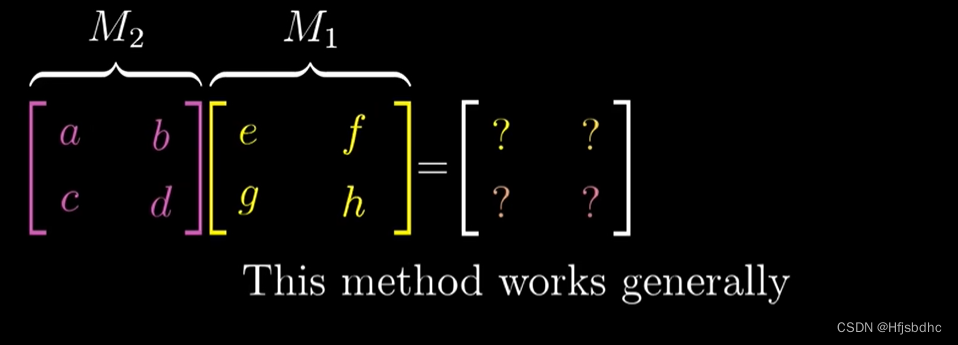
这种方法符号繁多,也需要更多空间
但是那些曾经通过书面计算学习矩阵乘法的人来说是非常满足的
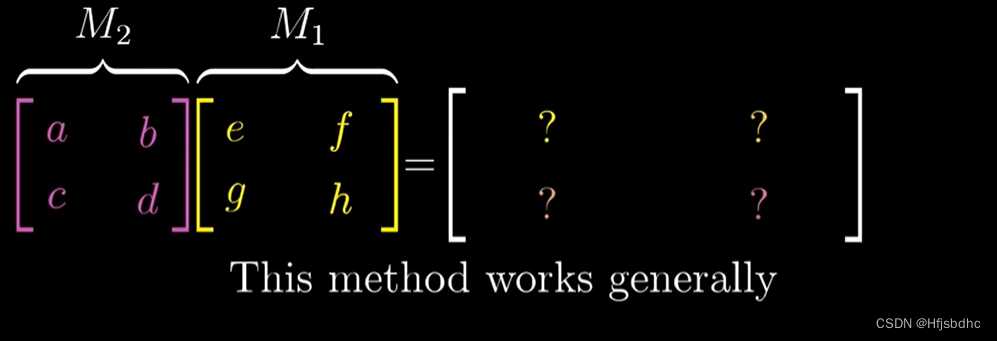
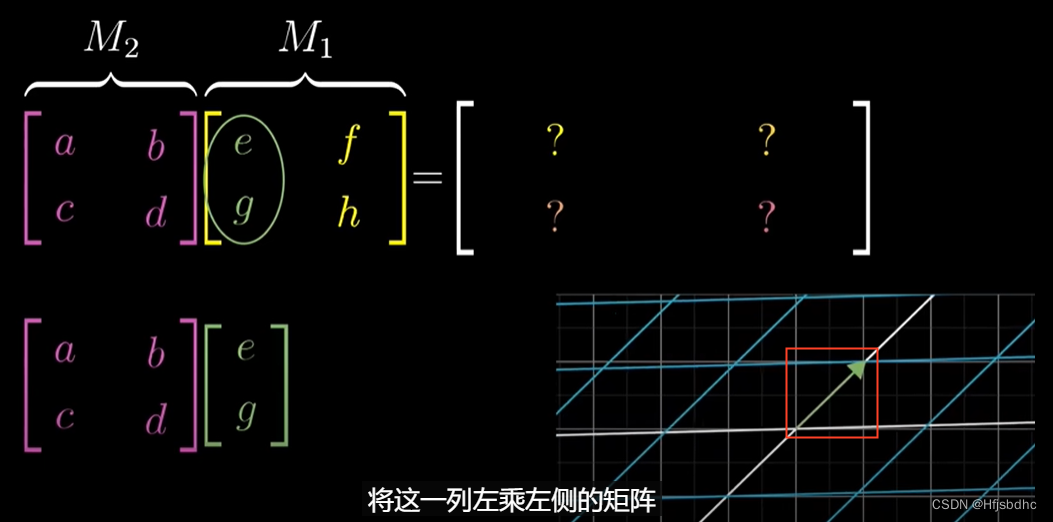
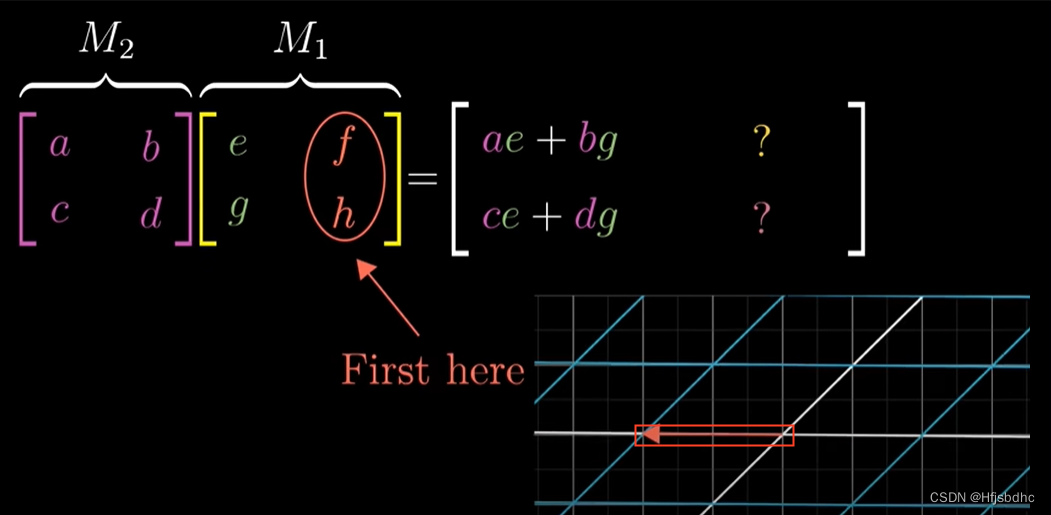
要跟踪i帽的去向,首先找右侧矩阵的第一列
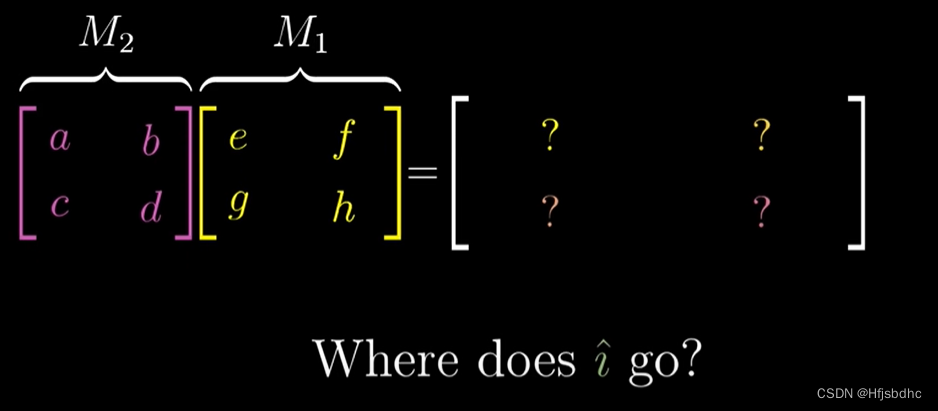

因为这是i帽首先到达的地方

将这一列左乘左侧的矩阵
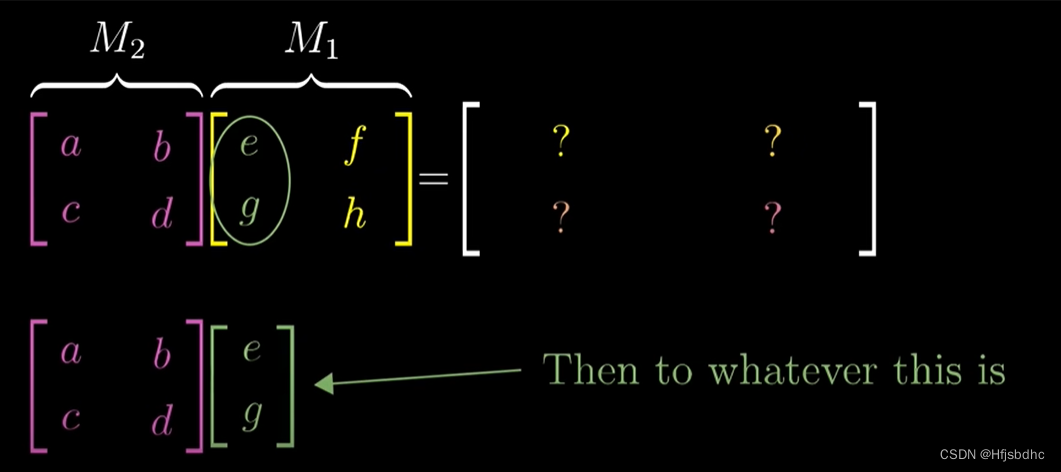
结果就是i帽在第二个变换作用后的结果
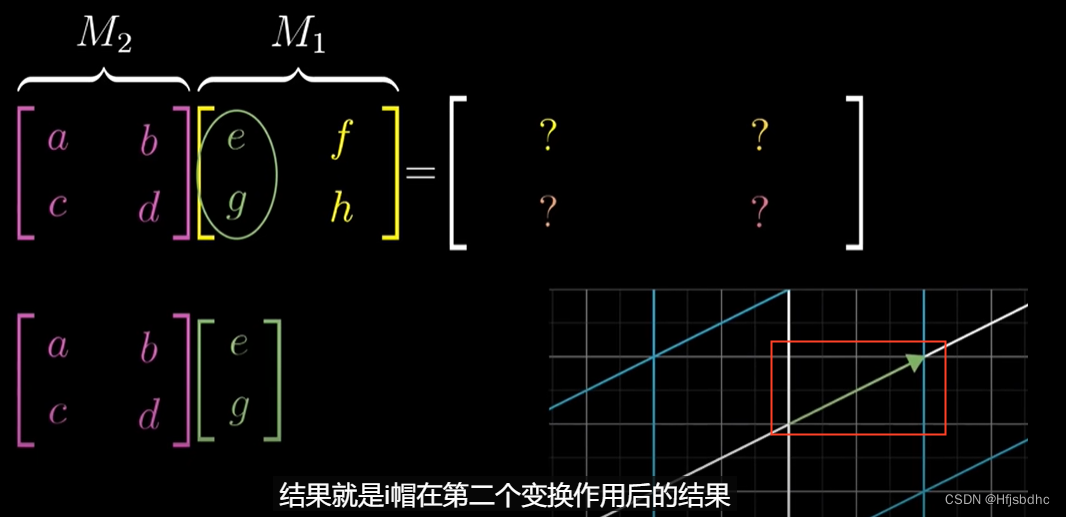
所以复合矩阵的第一列
就是左侧矩阵与右侧矩阵第一列的乘积
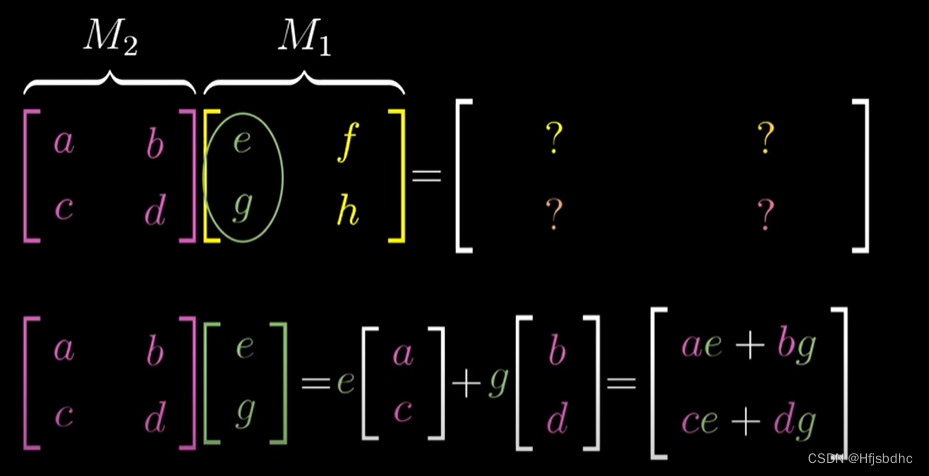
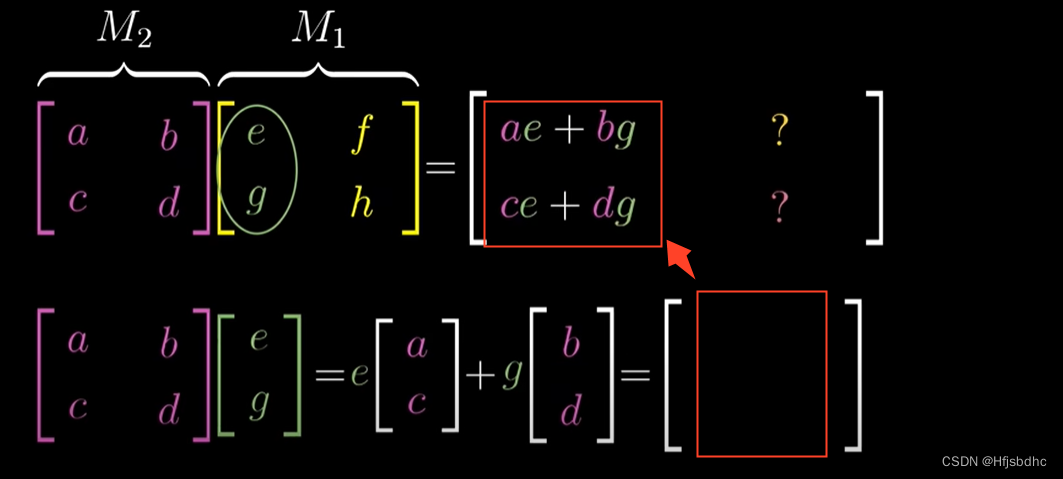
类似地,j帽首先落在右侧矩阵第二列所代表的位置上
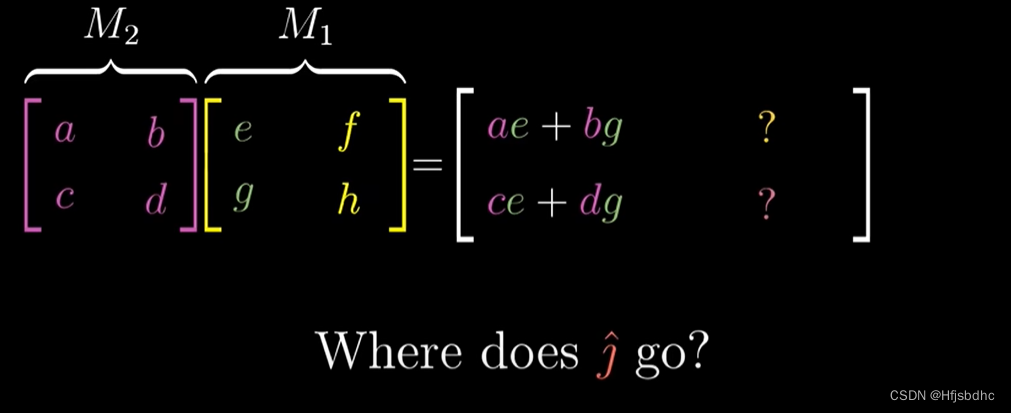
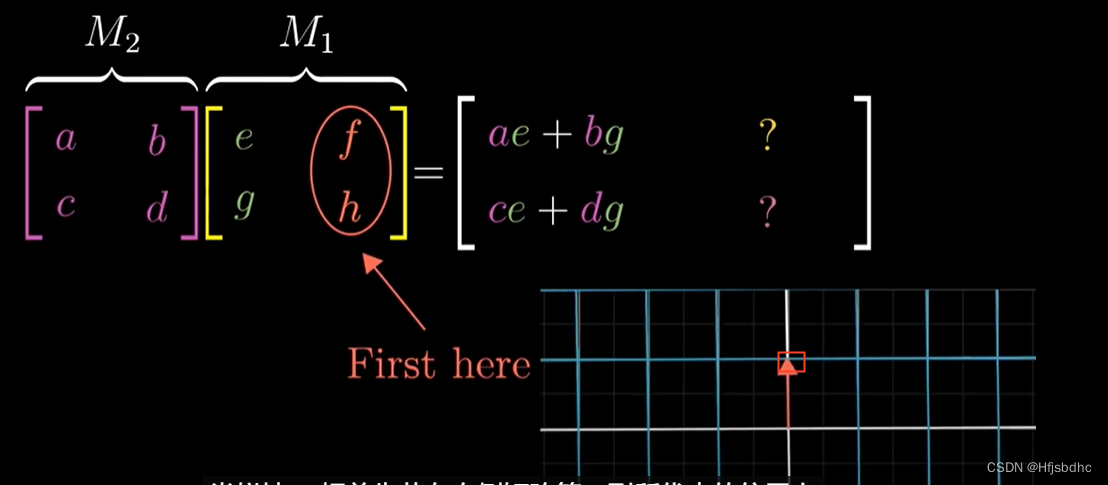
左侧矩阵与这一列相乘就能得到j帽的最终位置
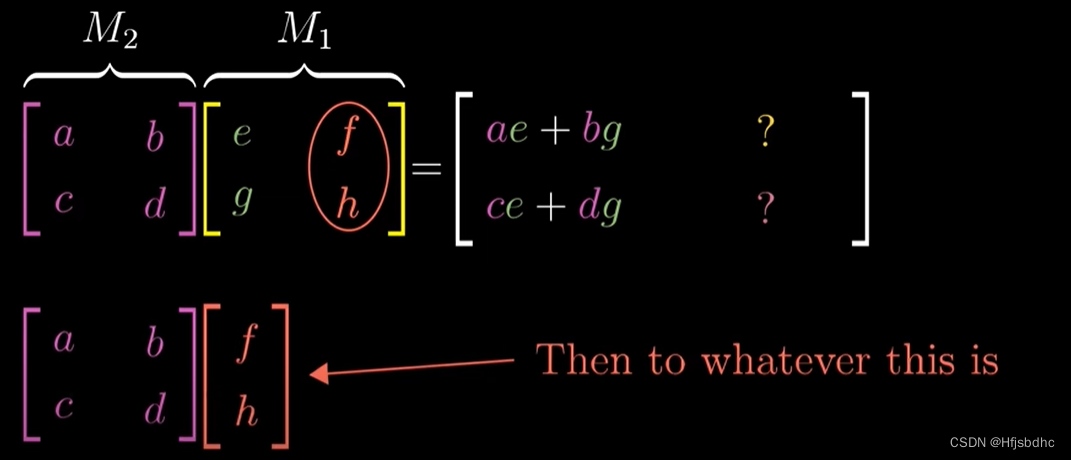


因此这一乘积就是复合矩阵的第二列
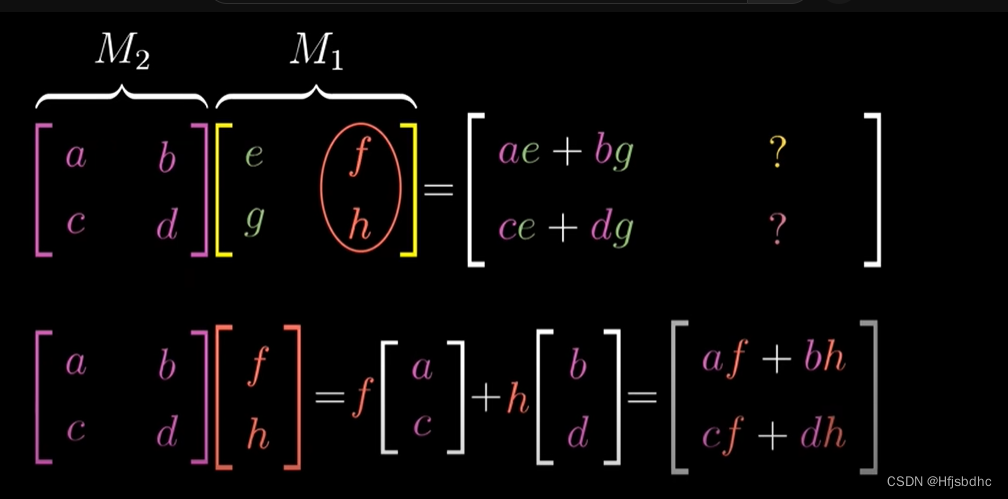
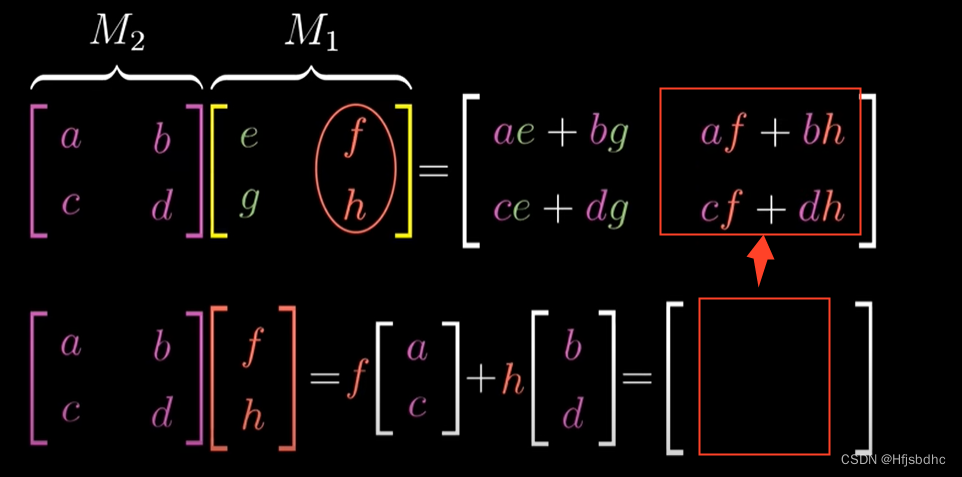
注意,这里有不少符号,通常学生需要记住这个公式
并通过一些特定的运算加强记忆
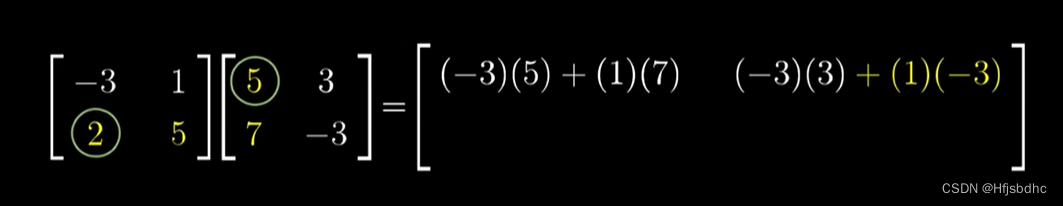
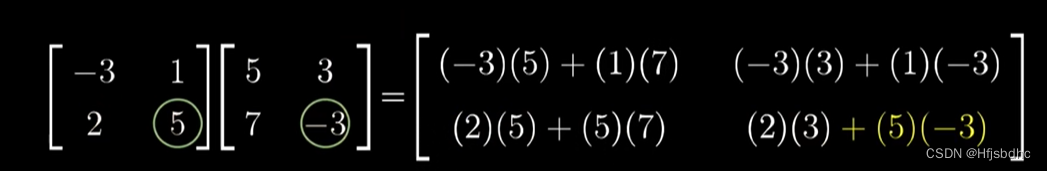
但是在记忆这个过程前
我认为你应该养成思考矩阵乘法意义的习惯
也就是两个变换相继作用
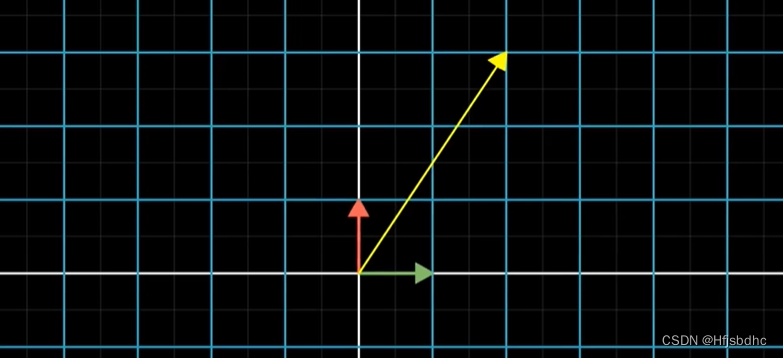
第一次变换
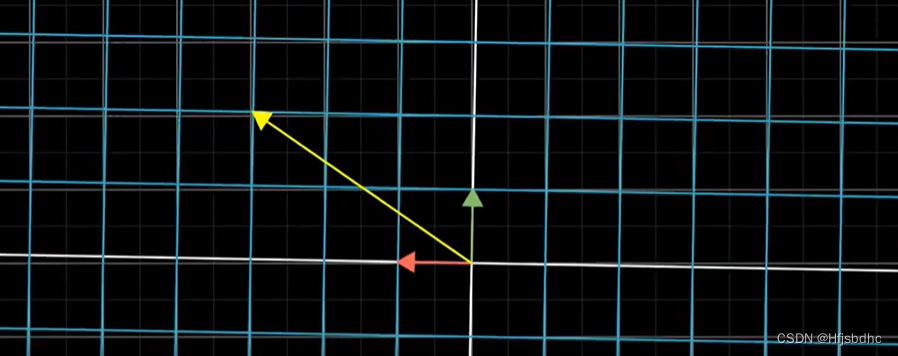
第二次变换
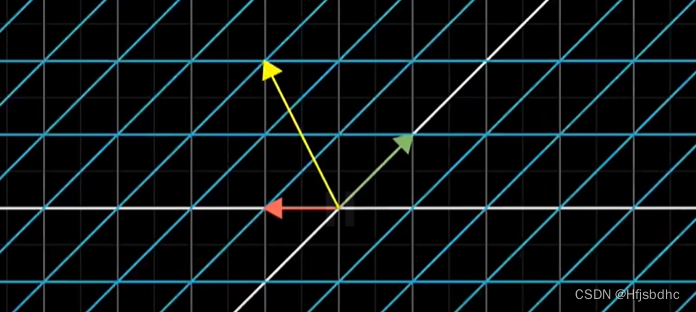
相信我,这能给你一个更好的概念性框架
并让你更容易理解矩阵乘积的性质

比如说下面这个问题
矩阵相乘时,它们的先后顺序影响结果吗?
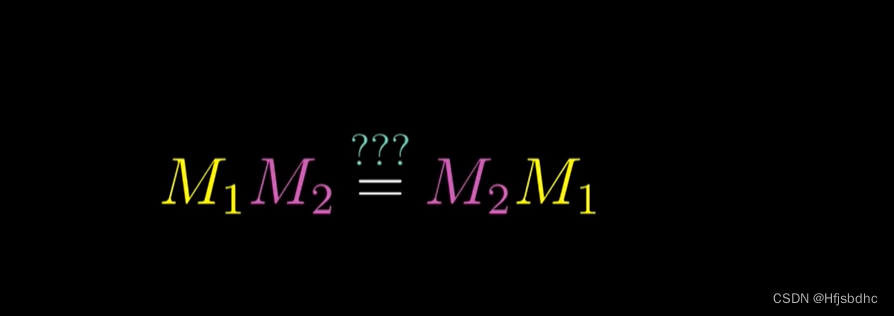
我们先来想一个简单的例子,比如之前提到的
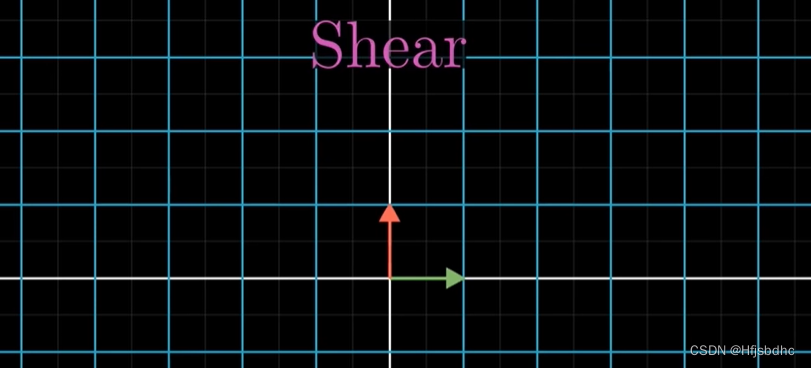
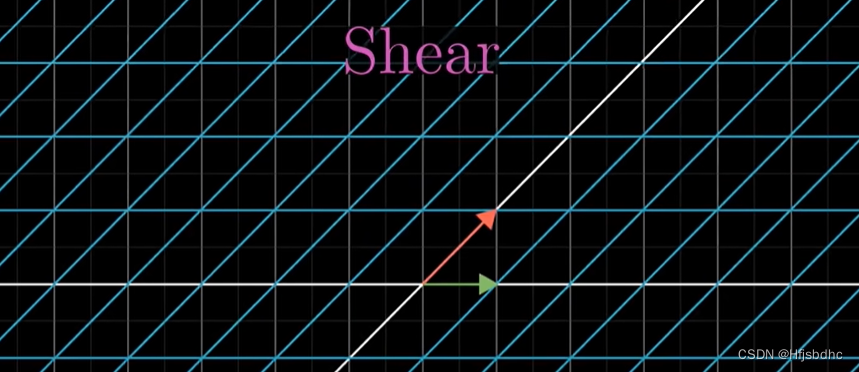
一个是剪切,它保持i帽不变,将j帽挤到右边
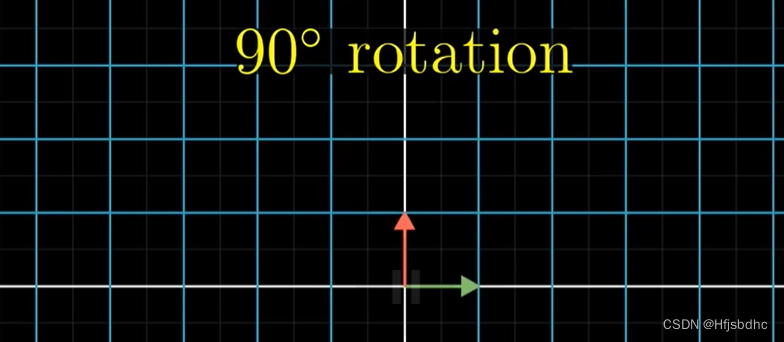
一个是90度旋转
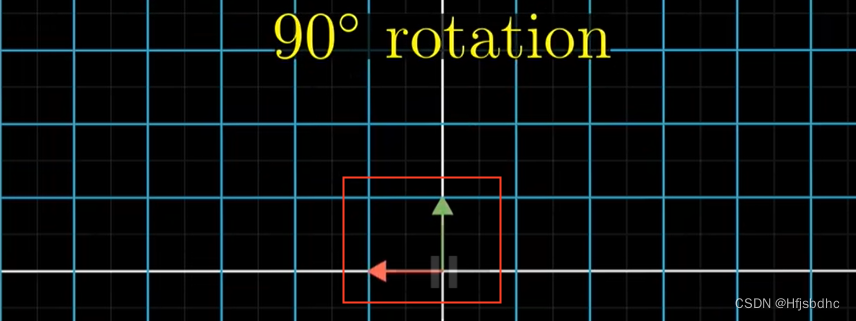
如果你首先剪切,

然后旋转
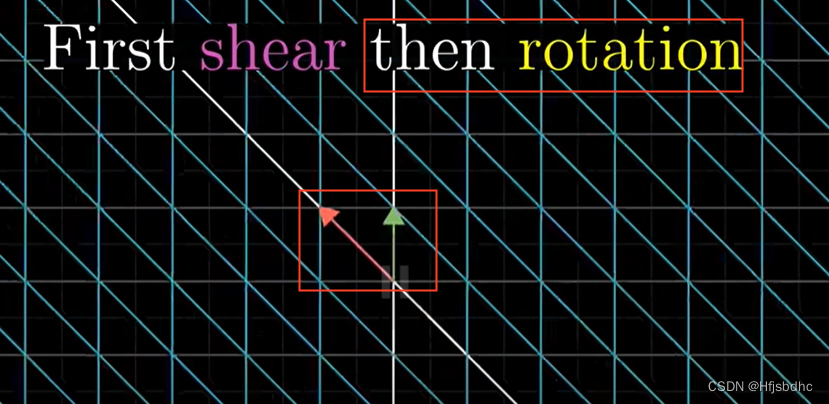
你会发现i帽落在(0, 1),j帽落在(-1, 1)
它们彼此靠得很近

如果你首先旋转,
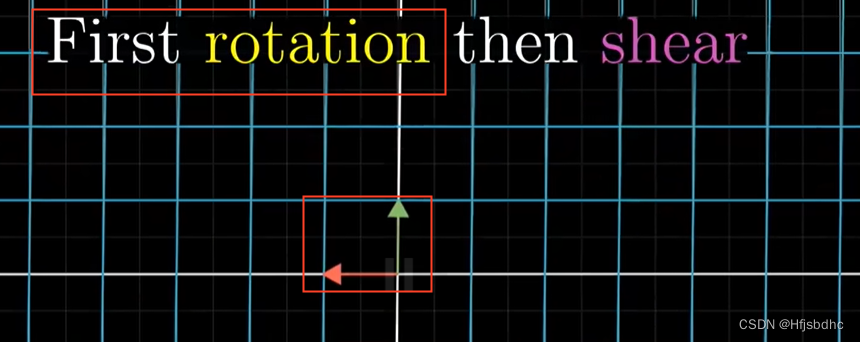
然后剪切
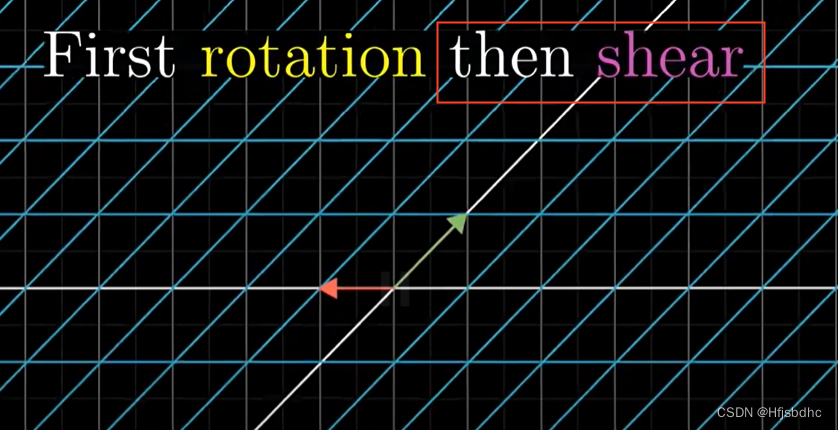
i帽落在(1, 1),而j帽落在一个不同的方向(-1, 0)
它们的指向分隔很远
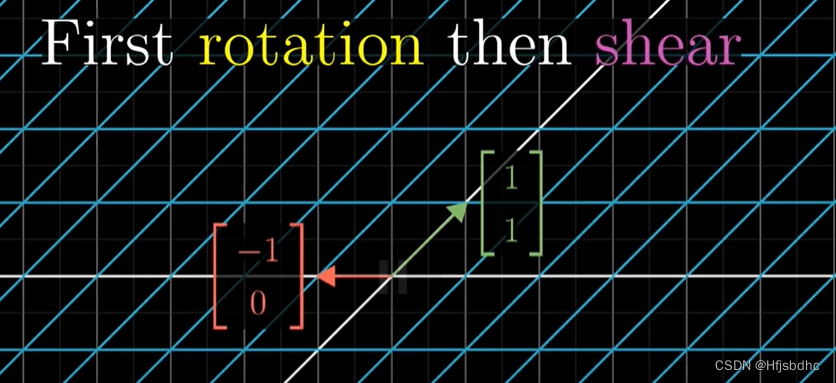
二者总体效应明显不同,所以乘积顺序显然会有影响
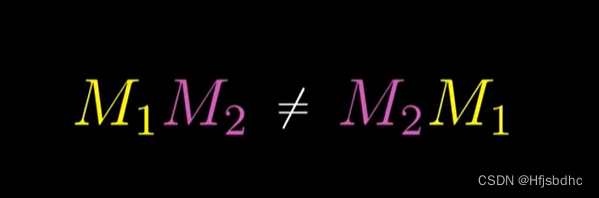
注意,我们用在变换来思考
这一过程可以在脑中形象地进行
完全不需要做矩阵乘法

我记得我首次学习线性代数时,有一道作业题是
让我们证明矩阵乘法具有结合性
这是在说,如果你有三个矩阵A B C,然后将它们相乘
无论是首先计算A乘以B,然后将结果乘以C
还是先算B乘以C,然后将结果左乘A,二者结果应该相同
换句话讲,添加括号与结果无关
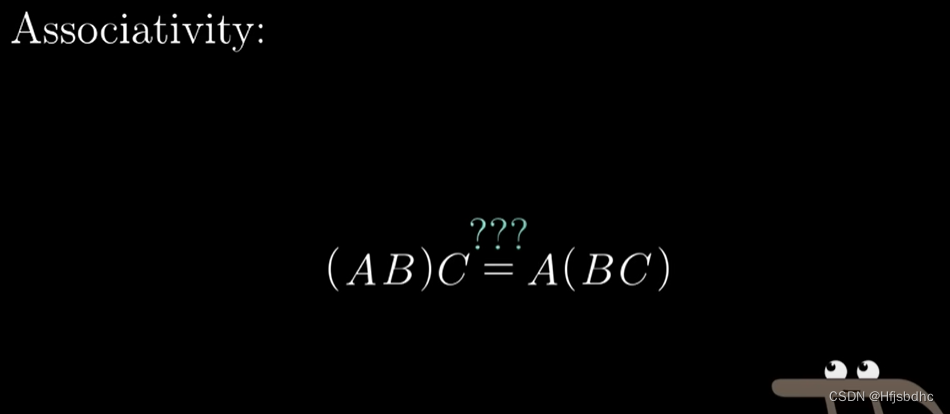
现在如果你尝试用数值方法证明,就像我当时所做的
这个过程会非常糟糕,而且对你毫无启发
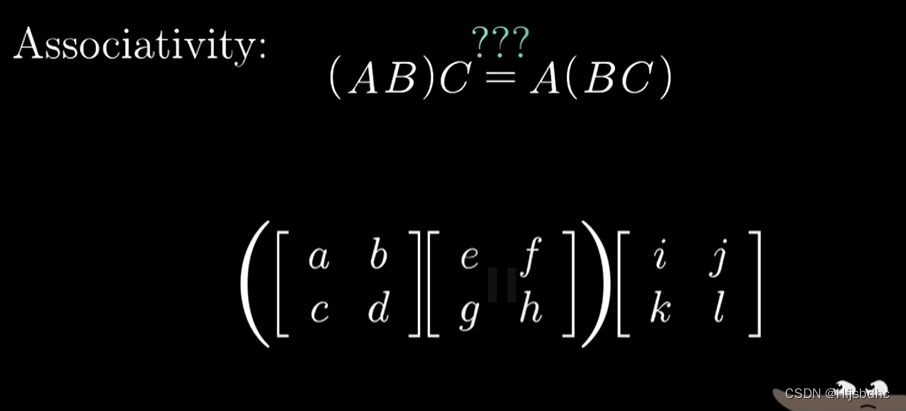
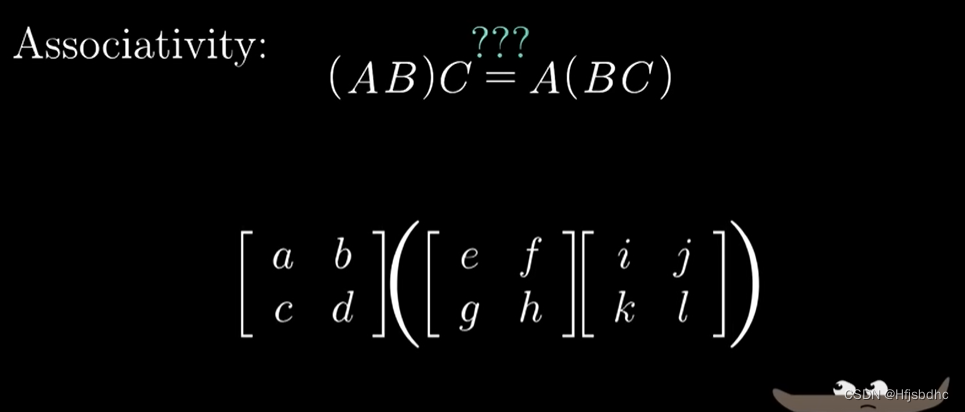
但是如果你用变换相继作用的思想去考虑矩阵乘积
这一性质就变得很平凡了
你能看出为什么吗?
这是在说,首先应用C变换和B变换,然后应用A变换
下面是A(BC)
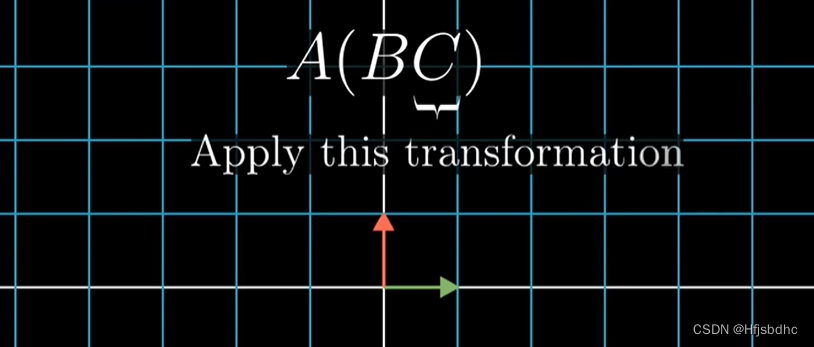


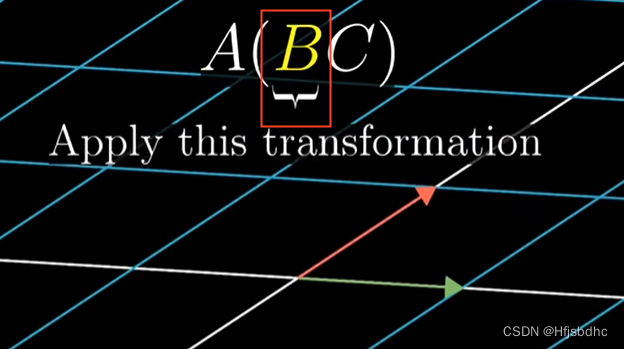
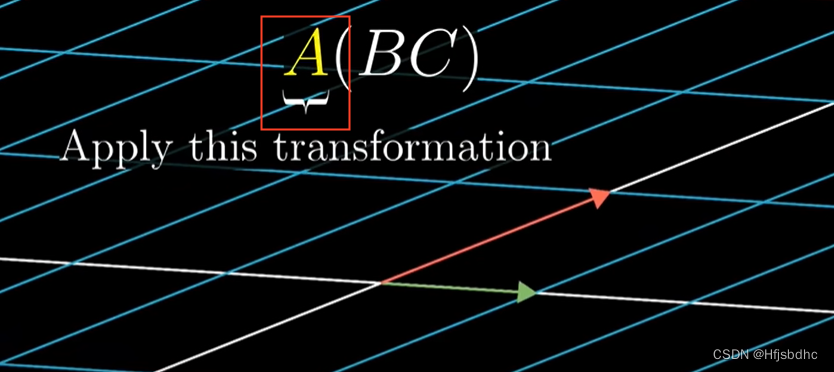
与先应用C变换,然后应用B变换和A变换的结果相同
下面是(AB)C


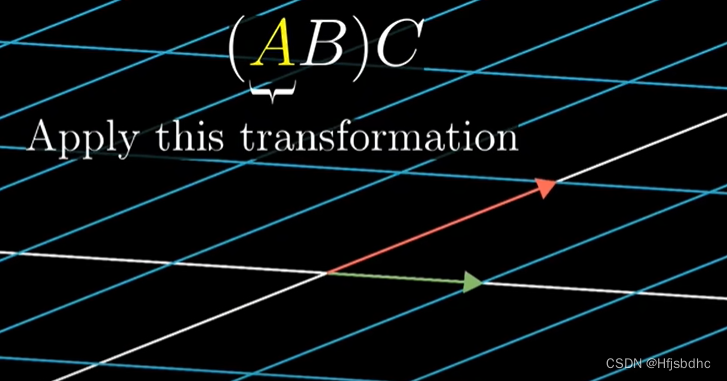
完全没有需要证明的东西
你只是将同样的三个变换用同样的顺序依次作用而已
顺序还是一样的
可能这看起来是在耍花招,但并不是
这是证明矩阵乘法具有结合性的一个实实在在的证明
它甚至很好地解释了为什么这个性质应该是正确的

我真的鼓励你在这种想法上多做尝试
想象两个不同的变换
思考他们依次作用后会发生什么
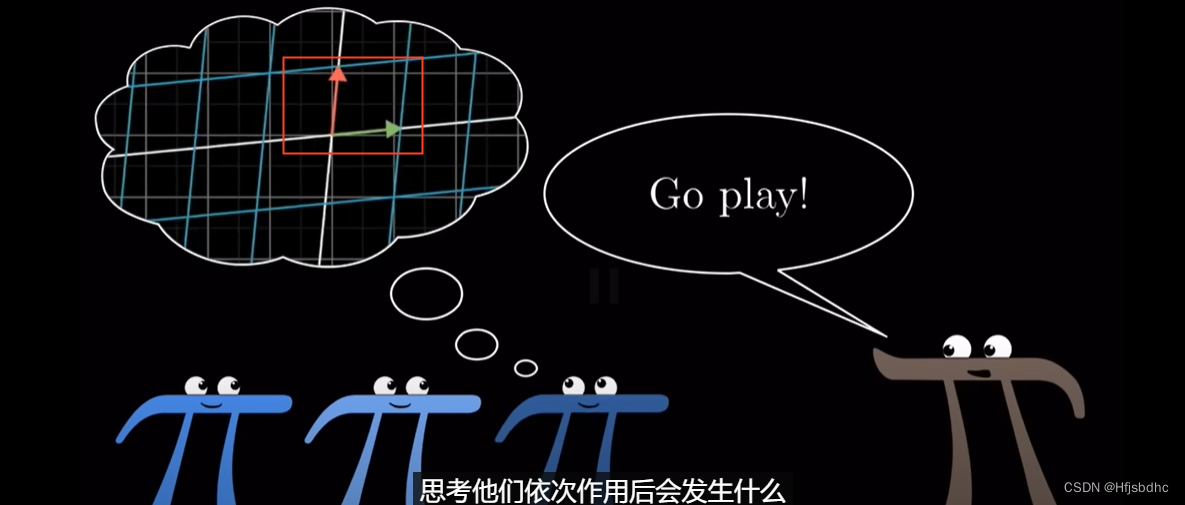
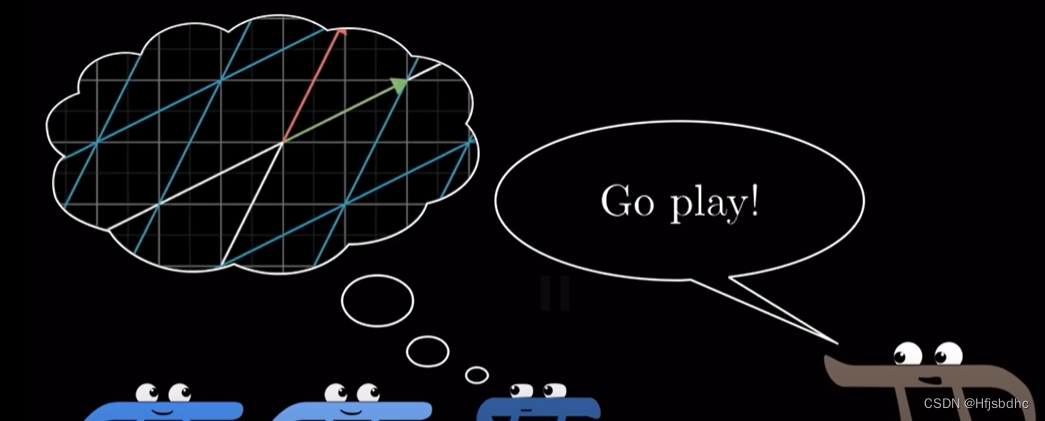
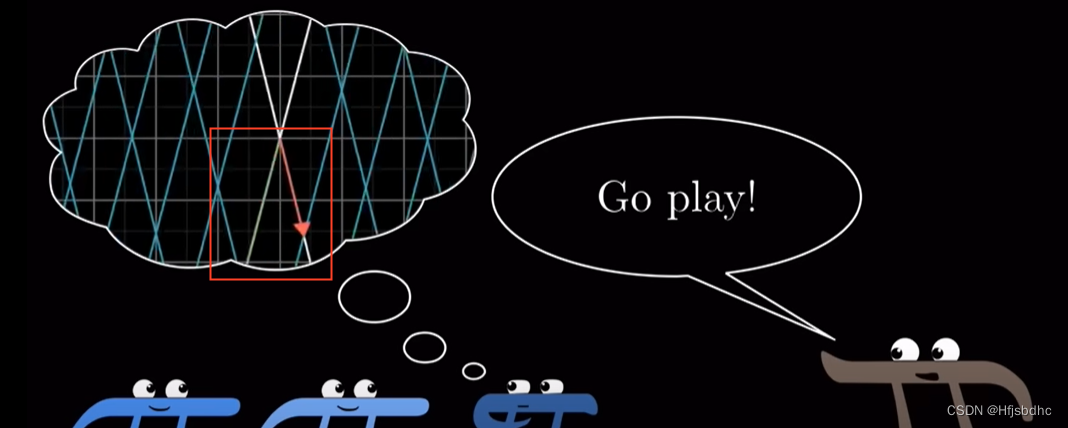
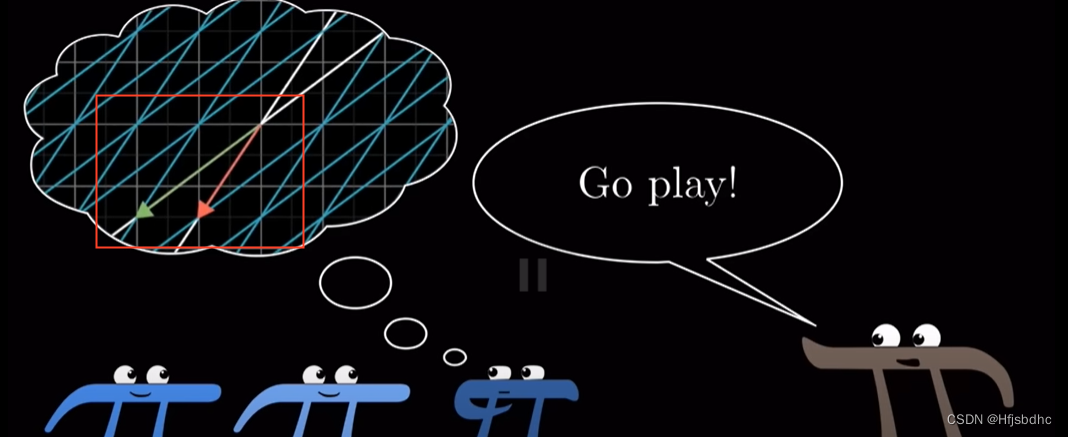
最后用数值方法计算出矩阵乘积
相信我,这段时间能让你完全理解这一想法
下期视频中,我会将二维空间中的这些想法拓展至三维空间中
到时候再见!
(下期视频:三维空间中的线性变换)

这篇关于【线性代数的本质 - 系列合集】04 矩阵乘法与线性变换复合的联系(万字详文)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





