线性代数学习笔记（二）：线性变换的理解

本文主要是介绍线性代数学习笔记（二）：线性变换的理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

线性代数学习笔记（二）：线性变换的理解

一、基变换与坐标变换

一个n维的线性空间V，可以有多组基底。
假设存在两组基底：老基底$=({\vec{e}}_1,{\vec{e}}_2,...,{\vec{e}}_n)$；
              新基底$=({\vec{e}}_1^{\prime },{\vec{e}}_2^{\prime },...,{\vec{e}}_n^{\prime })$。
对于线性空间中一个元素$\vec{\alpha }$可以被表示，如下图示：也即元素$\vec{\alpha }$=

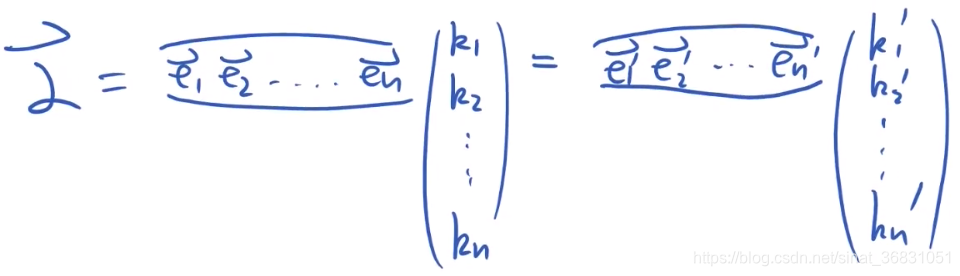
我们知道对于新基底中每个元素${\vec{e}}_k$，其都属于线性空间V中的某一个普通元素，所以可以用老基底展开表示出来，如下图：

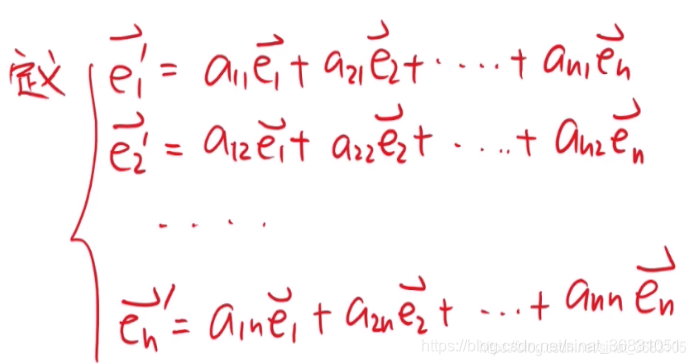
将系数抽象出来，用矩阵表示-矩阵T：

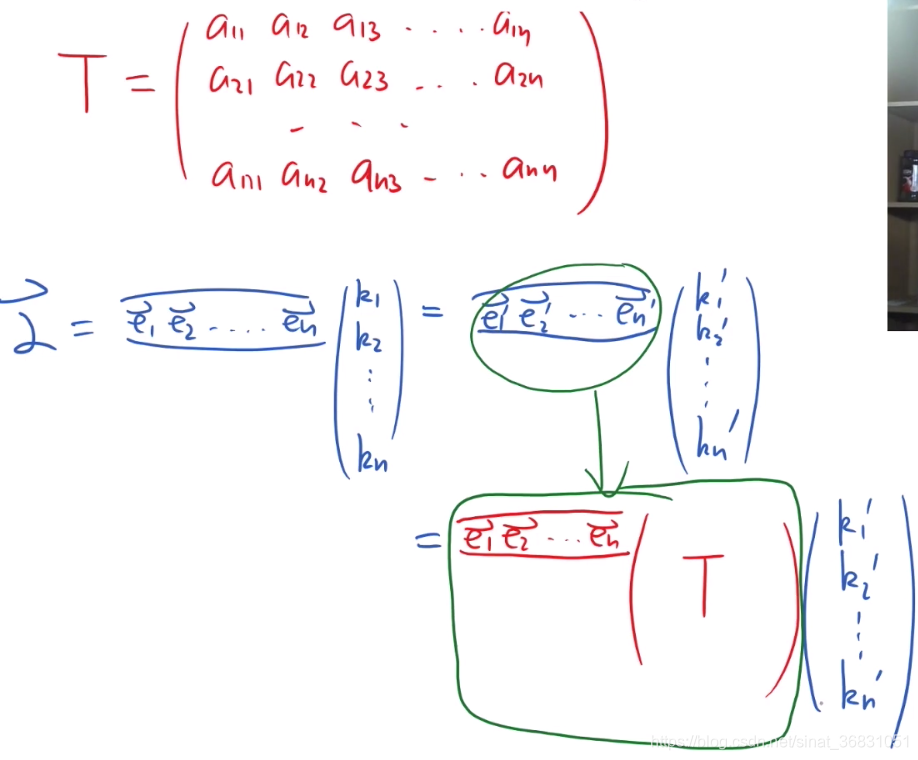
观察可得：
基变换：$({\vec{e}}_1^{\prime },{\vec{e}}_2^{\prime },...,{\vec{e}}_n^{\prime })=({\vec{e}}_1,{\vec{e}}_2,...,{\vec{e}}_n)T$
系数变换：$({\vec{k}}_1,{\vec{k}}_2,...,{\vec{k}}_n)=({\vec{k}}_1^{\prime },{\vec{k}}_2^{\prime },...,{\vec{k}}_n^{\prime })T$
其中，T 被称作过渡矩阵。
(不区分基底变换矩阵和系数变换矩阵，同是矩阵T[好巧(´∀`)])。
那么再来想，如果$({\vec{e}}_1^{\prime },{\vec{e}}_2^{\prime },...,{\vec{e}}_n^{\prime })$可以作为线性空间V的一组新基底。那它肯定需要满足：线性无关性。
根据基底变换公式：新基底=老基底*T。
得：新基底的线性无关性与转换矩阵T有关。
    —— T是满秩矩阵。

基底变换矩阵可以由老基底变到新基底，同样也一定能由新基底再变回来。那么就引出了 “矩阵的逆”-“逆矩阵” 的概念。
如下图所示：


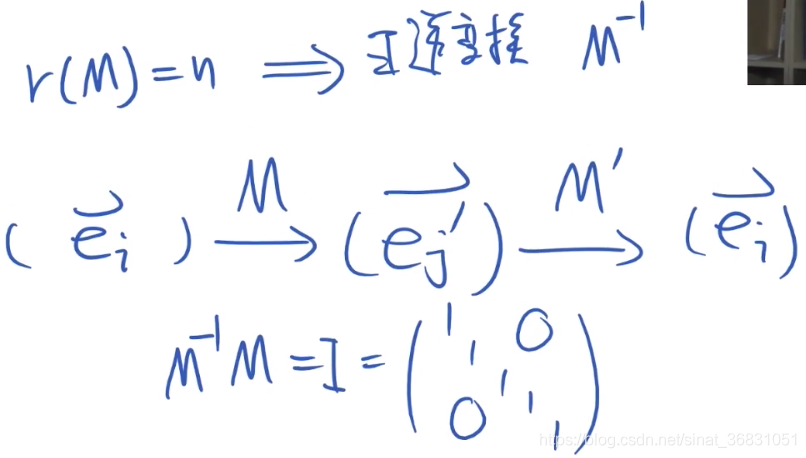
可以得到结论：

$rank(T)=n$ ;
矩阵T是方阵，同时是可逆矩阵。

二、 线性变换

2.1 线性变换与基变换的不同

2.1中为引入“基变换”和“坐标变换”的概念，从线性空间拎出任一向量$\vec{\alpha }$，并对这一个向量的“微观”表示下文章，加以解释概念。

向量不变，基底变。

而我们要从线性空间中取出的向量也不总是一成不变的，向量与向量间如何转换？

向量变，且变换后的向量仍保持线性性。

线性变换：
$L(k\vec{\alpha }+l\vec{\beta })=k\ast L(\vec{\alpha })+l\ast L(\vec{\beta })$

常见的线性变换：投影、旋转、反演、各类复合。

投影：$\vec{\alpha }$与$\vec{\beta }$的和在平面上的投影等于$\vec{\alpha }$与$\vec{\beta }$分别投影之和。

2.2 线性变换的表示

线性变换本身是不需要基底的，但是我们常常需要引入基底来帮助计算和形象化的表示这种变换。

• Why？
  想象一个二维空间中的向量$\vec{\alpha }$：对其做线性变换（伸缩或旋转、改变方向或大小）时，本就是针对这个向量本身完成的这些操作。但是为了具象的描述这个过程，引入基底以精准的用数学语言描述：
  已知二维空间的基底为$\vec{x}和\vec{y}$，$\vec{\alpha }$可以分别投影到x轴和y轴上，自然的定义一种数学描述$\vec{\alpha }=k\vec{x}+l\vec{y}$。
  当对$\vec{\alpha }$做整体线性变换$L(\vec{\alpha })$时，$L(\vec{\alpha })=L(k\vec{x}+l\vec{y})$,这个操作就相当于对每个基底(分量)先进行线性变换然后求和得到$L(\vec{\alpha })$：$L(k\vec{x}+l\vec{y})=k(L\vec{x})+l(L\vec{y})$。
  要想求$\vec{\alpha }$线性变换后的向量，先求出各个基底的线性变换后乘系数加和。

线性空间中引入基底来描述线性变换的过程:
$\vec{e}=({\vec{e}}_1,{\vec{e}}_2,...,{\vec{e}}_n)$
$\vec{\alpha }=k_1{\vec{e}}_1+k_2{\vec{e}}_2+...+k_n{\vec{e}}_n$
$L(\vec{\alpha })=k_1\ast L({\vec{e}}_1)+k_2\ast L({\vec{e}}_2)+...+k_n\ast L({\vec{e}}_n)$
研究$L(\vec{\alpha })$的问题转化成研究各个基底的线性变换。

观察每个基底的变化：${\vec{e}}_i\to L({\vec{e}}_i)$
每个基底也可以被原线性空间的一组基底表示(只不过其他维度系数都为0)
$L({\vec{e}}_i)$相当于对${\vec{e}}_i$ 这个基向量的 每个基底做线性变换。即每个分量乘上对应变换系数。

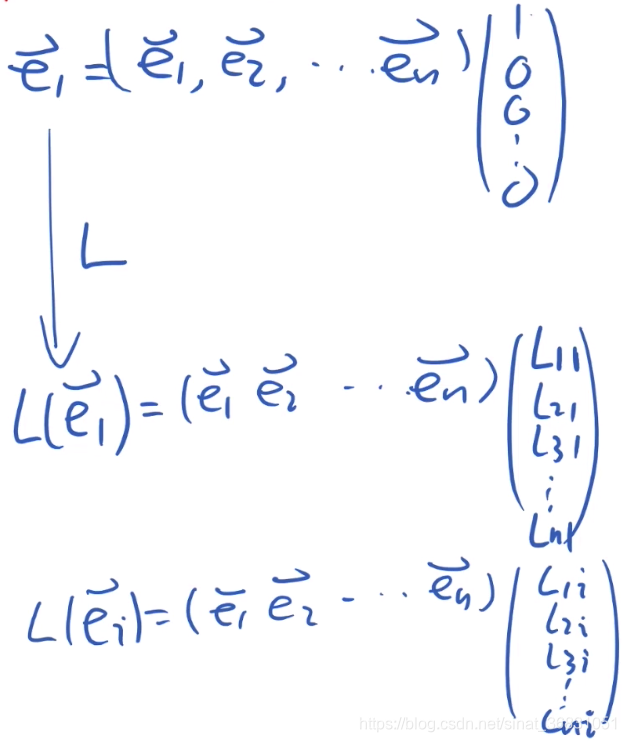
最终表示出对于这个向量而言，整体的线性变换—— 将线性变换L描述成一个矩阵$L_{n\ast n}$。

线性变换作用在一个向量上，就相当于作用在这个向量对应的每个基底上。

任何一个n*n的矩阵L，等价于一个线性变换。

2.3 线性变换的分类

线性变换根据是否可逆，分成可逆线性变换和不可逆线性变换。
可逆线性变换：旋转、反演等。
不可逆线性变换：投影。

2.4 线性变换与矩阵

在学习线性空间和线性变换的过程中，我们总不可避免的去接触矩阵这个东西——
a) 描述坐标变换${\vec{e}}_i\to {\vec{e}}_i^{\prime }$，用到矩阵$T_{n\ast n}$；
b) 描述向量用不同基底展开时的系数变化$k_i\to k_i^{\prime }$，用到矩阵$T_{n\ast n}$；
c) 描述线性变换$\vec{\alpha }\to {\vec{\alpha }}^{\prime }$，用到矩阵$L_{n\ast n}$。

那矩阵到底是什么？到底用来描述什么东西？
想象一个自然数，我们可以把它认为是多少钱、多少道题、多少本书、多少天等。

当给定了使用场景/衡量标准时，它有不同的意义。
只有给定了使用场景/衡量标准时，它才有意义。
矩阵也是这样。

对于矩阵的理解要结合具体场景，从宏观体系上理解。眼光不能总是聚焦在矩阵中的一串数字上。

2.5 应用：线性代数观点看线性变换

用线性代数求解函数空间中的线性微分方程
在这里要引出对相似矩阵的概念理解

2.5.1 微分方程是线性变换

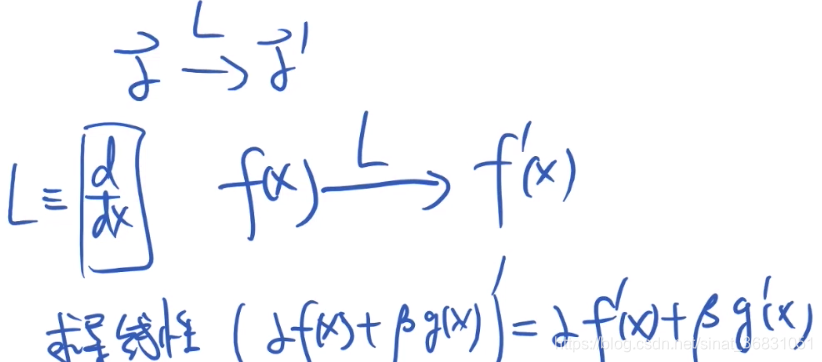
2.5.2 傅里叶变换是基底变换

傅里叶变换的思想：
如果直接求解微分方程不会做，先把$f(x)$经过傅里叶变换(基底变换)成$g(k)$，再对$g(k)$求解。
问题简化成“解多项式方程”。

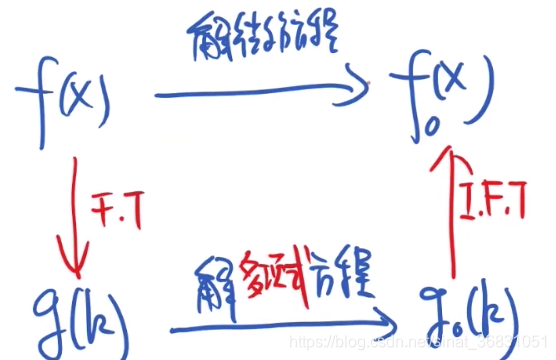
时域空间中$f(x)$与频域空间中$g(k)$的关系：

为什么要将$f(x)$转成$g(k)$计算？
$g^{\prime }(k)=(-ik)g(x)$，发现：我们依然可以用g(k)来表示g(k)的导数。这样就可以将微分方程$\to$多项式方程，解起来简单多了。

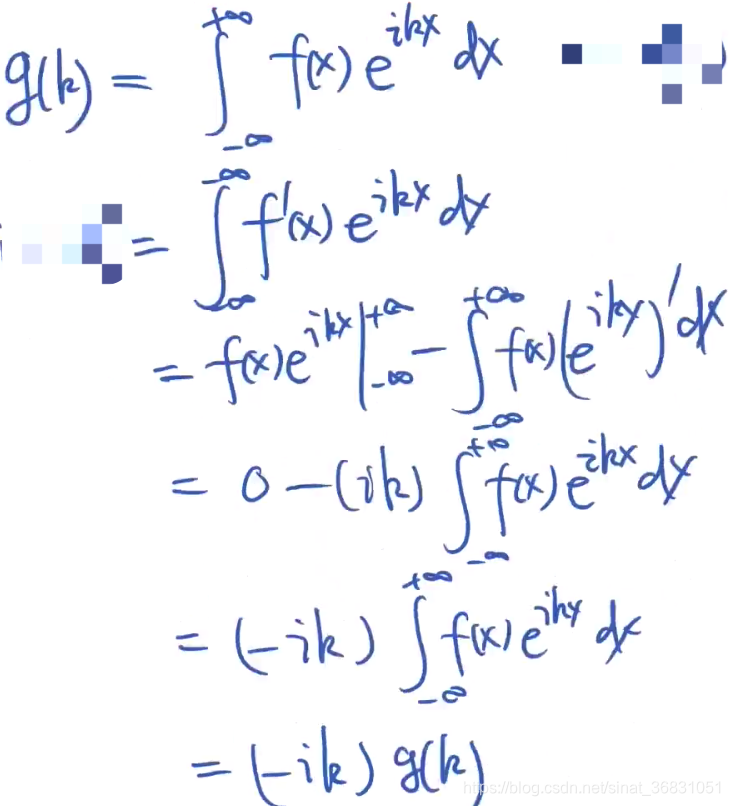
-eg：
求解线性微分方程$f^{\prime \prime }+3f^{\prime }+2f=0$。

2.5.3 相似矩阵

依据前面利用傅里叶变换求解问题的思想：
拿到一个问题，正面直接求解我们不会做。
但若存在一种转换方法，将原问题转化成另外一个问题，又能将问题再转换回原问题。并且这种转换方法往往使得计算更简单。
在这个变换过程中，注意T必须是可逆的。

• 根据这种思想，得到相似矩阵的概念：

若$A=T^{-1}BT$，则称A相似于B。

单对数学表达式进行观察，我们似乎很容易得到：“一个矩阵B 与 对其右乘矩阵T再左乘矩阵T的逆矩阵得到的矩阵A相似”这种表面上的定义方式，但更应该清楚这到底是怎么得来的，以及为什么要有这种定义和操作。

三、线性空间的理解

详见：
线性代数学习笔记（一）：线性空间的理解

四、矩阵的理解

详见：
线性代数学习笔记（三）：矩阵的理解之— 矩阵的秩与行列式

线性代数学习笔记（四）：矩阵的理解之— 矩阵的特征值与特征向量

线性代数学习笔记（五）：矩阵的理解之— 线性代数核心定理

这篇关于线性代数学习笔记（二）：线性变换的理解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---