矩阵分析与计算学习记录-线性空间和线性变换

本章知识要点

线性空间：维数、基、坐标、基变换、坐标变换、线性相关线性无关，极大线性无关组、范德蒙德行列式；

线性空间的分解：子空间、值域(像空间)与核空间(零空间)、 秩与零度、子空间的交、和与直和；

线性变换及其矩阵表示：定义、运算、值域与核空间、秩 与零度、相似类、特征值与特征向量、不变子空间、同构。

首先这里介绍数域的概念

设P是由一些复数组成的集合，其中包括0与1，如果P中任意两个数的和、差、积、商（除数不为0）仍是P中的数，则称P为一个数域。

常见数域： 复数域C；实数域R；有理数域Q。

（注意：自然数集N及整数集Z都不是数域。）

说明：

1）若数集P中任意两个数作某一运算的结果仍在P中，则说数集P对这个运算是封闭的。

2）数域的等价定义：如果一个包含0，1在内的数集P对于加法，减法，乘法与除法（除数不为0）是封闭的，则称数集P为一个数域。

1. 线性空间

1.1 线性空间的定义和性质

 

 后面四条也是数乘矩阵运算的四条性质

在线性代数课程中，我们把有序数组称为向量，把 n 维 向量的全体所构成的集合 Rn 称为 n 维向量空间。

一般地，如果 V 为非空的 n 维向量的集合，且集合 V 对 于向量加法及数乘两种运算封闭，那么就称集合V为向量空间。

 除向量空间外的其他线性空间：

 举一些例子

 

 

 

 

 

 

   由此可以的得出线性空间的一般观点：

 1.2 线性相关和线性无关

 首先讨论向量的线性相关与线性无关：

 这里线性组合和线性表示是一组相关的问题。

线性表示/线性组合：设V是数域F上的线性空间，α1,α2,…,αr是V中的任意一组向量（其中r≥1），k1,k2,…,kr是数域F中的一组数。若向量α可以表示成α=k1α1+k2α2+…+krαr，则称α可由α1,α2,…,αr线性表示或线性表出，同时也可以称α是α1,α2,…,αr的线性组合。

线性相关/线性无关：设α1,α2,…,αr是线性空间V中的一组向量（其中r≥1）。如果在数域F中有r个不全为零的数k1,k2,…,kr，使得k1α1+k2α2+…+krαr=0，则称α1,α2,…,αr线性相关。如果一组向量α1,α2,…,αr不线性相关，就称为线性无关。换言之，若k1α1+k2α2+…+krαr=0当且仅当k1=k2=…kr=0，便称α1,α2,…,αr线性无关。一组向量要么线性相关，要么线性无关，非此即彼。

线性表出唯一定理：设线性空间V中向量组α1,α2,…,αm线性无关，且向量组α1,α2,…,αm,β线性相关，则β可由α1,α2,…,αm线性表出，且表出是唯一的。

 

 举个简单的线性组合的例子：

 

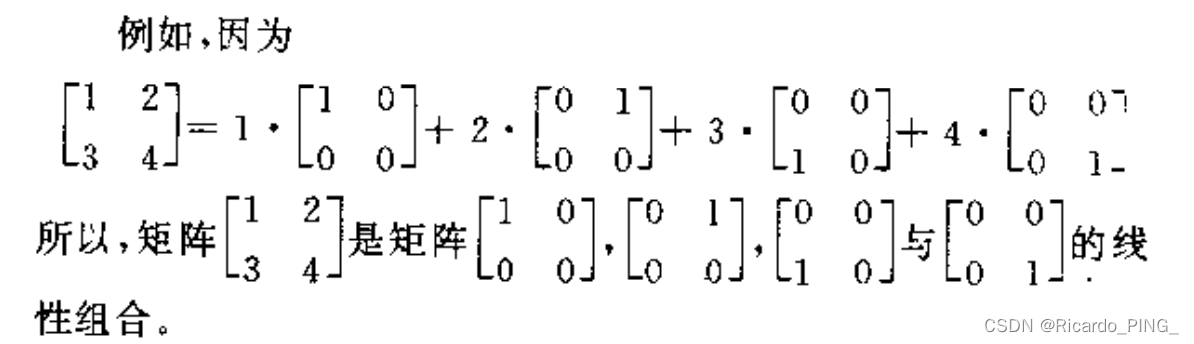
线性相关和线性无关问题： 

 

 举个例子证明：

 

 

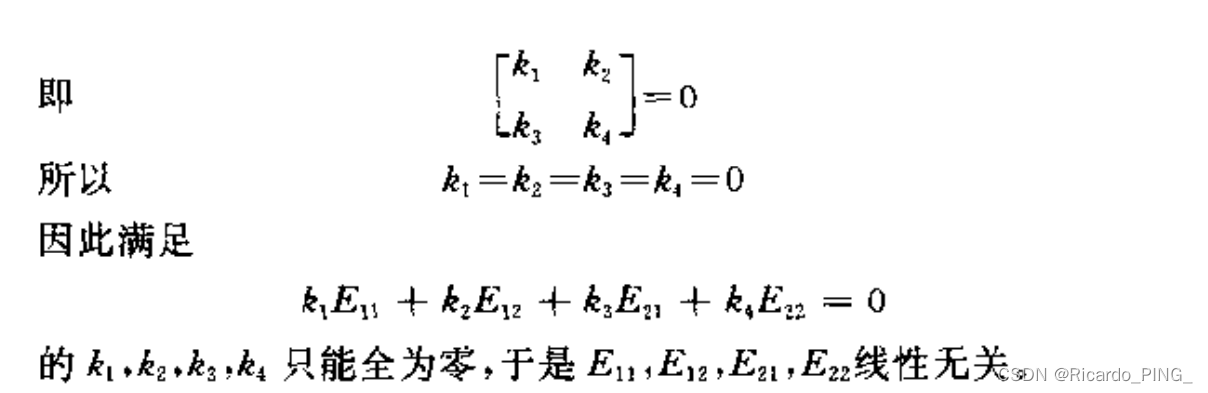
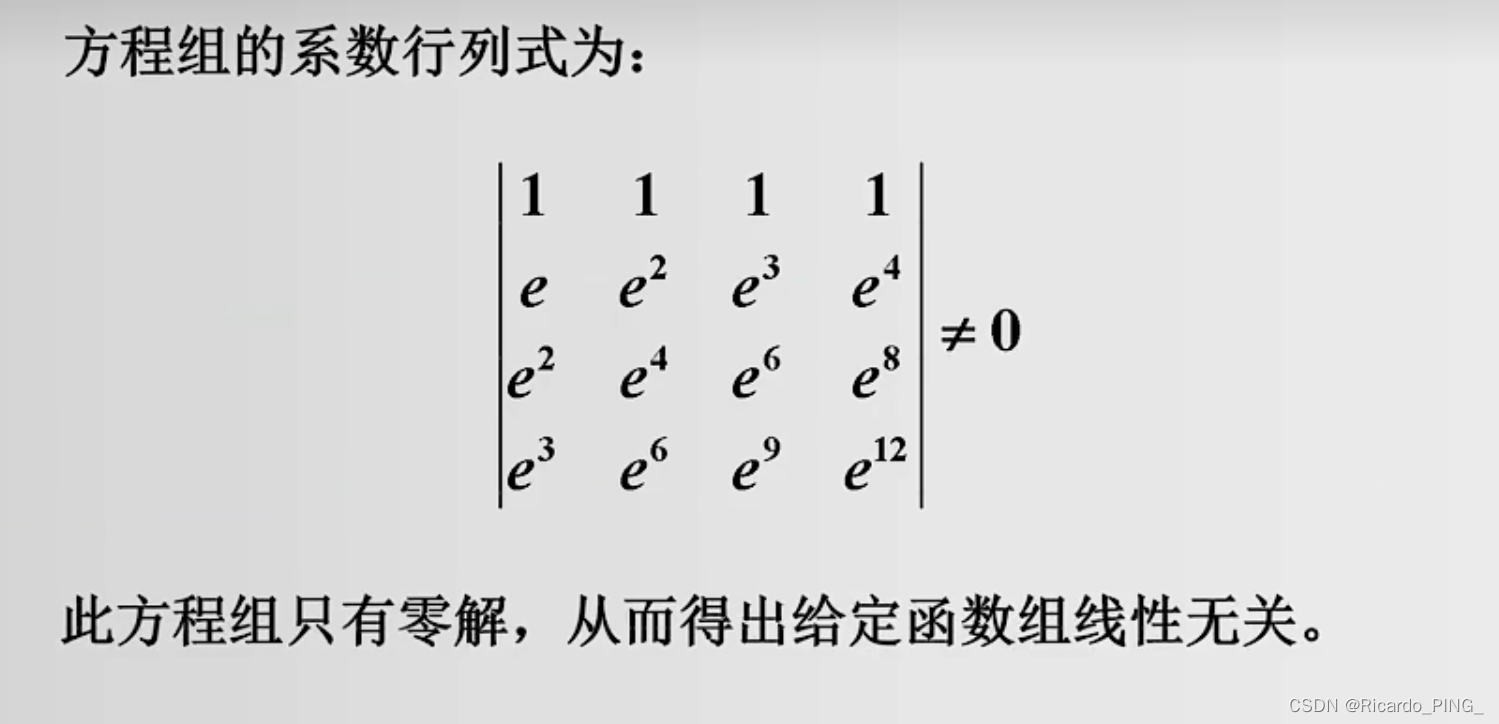
以上的行列式是范德蒙德行列式，以下给出其定义 

 

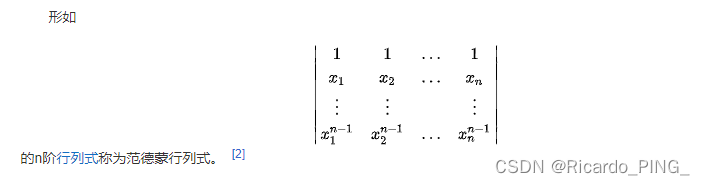
 同时可知范德蒙德行列式的结果是不为0的

 

向量组的极大线性无关组和秩

 

 极大线性无关组的基本性质

 

  1.3 基、维数与坐标

 

 

 

 下面是一题求基的例题

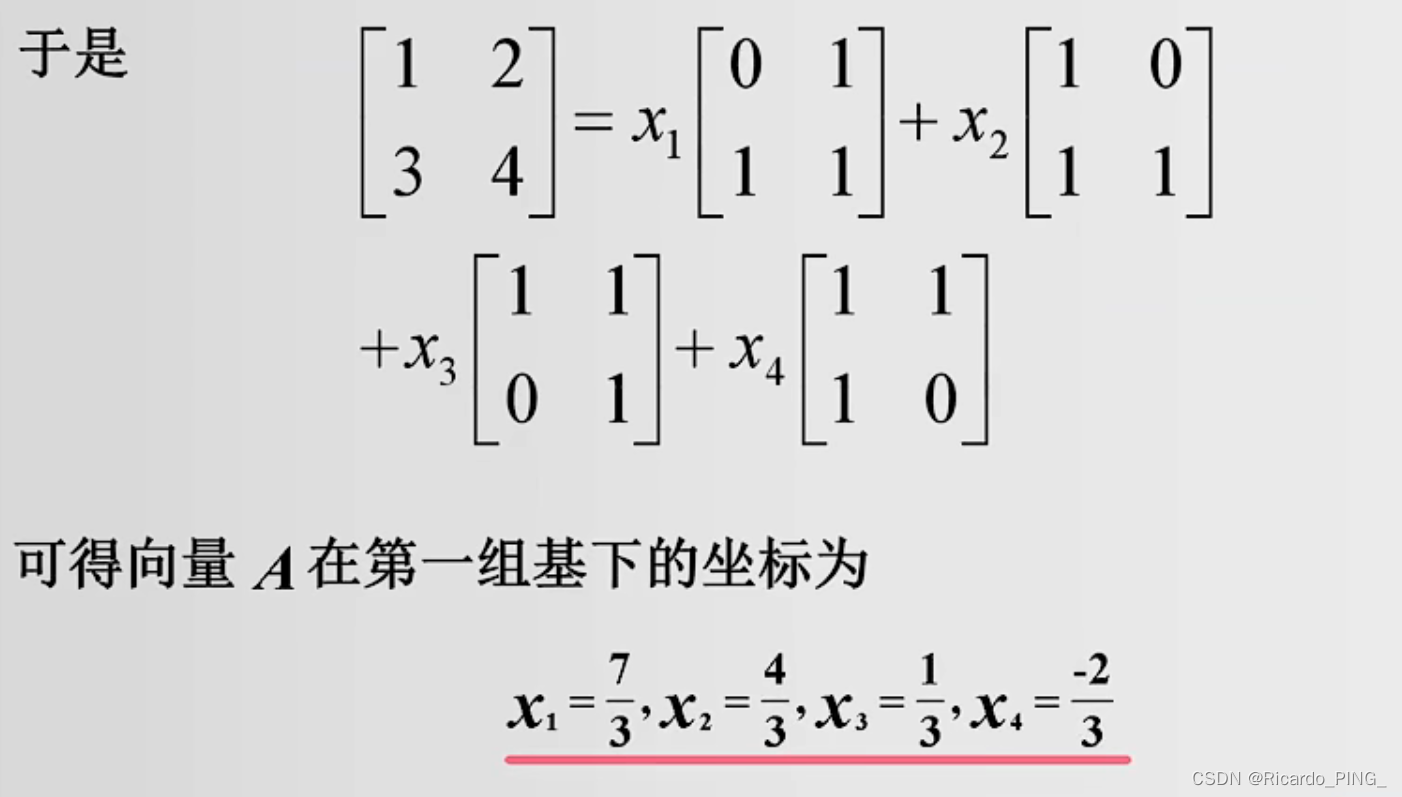
 下面是一题求坐标的例题

 

 

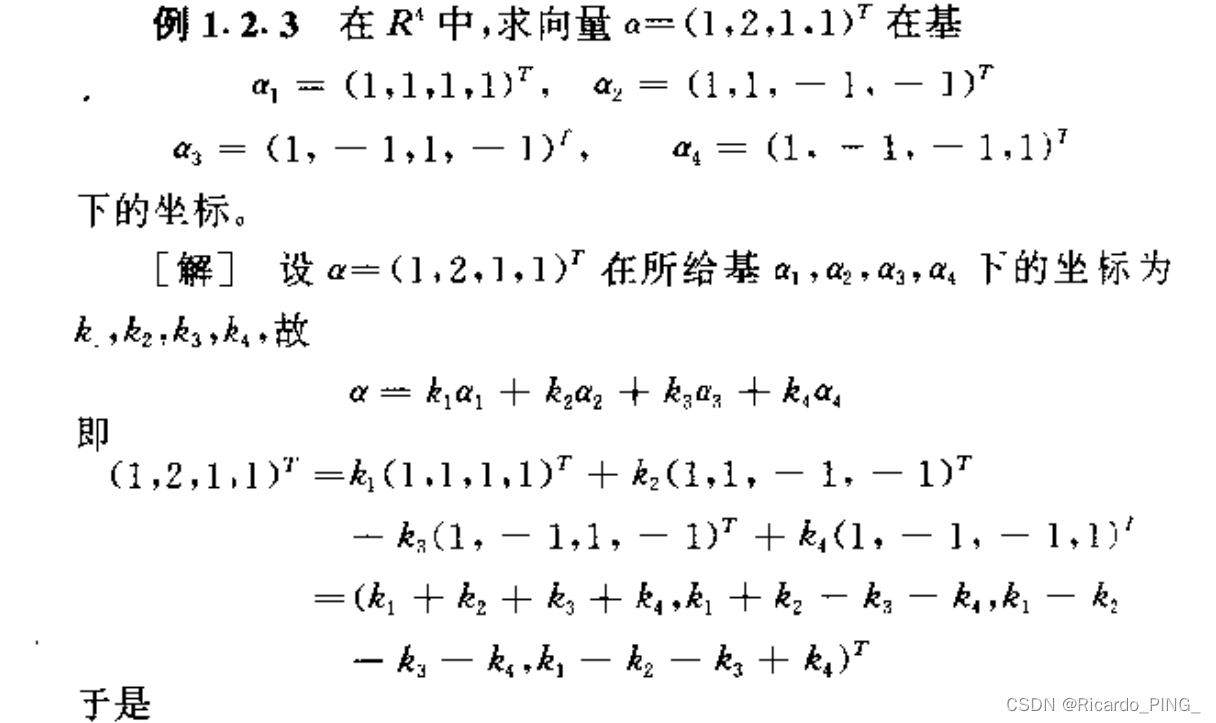
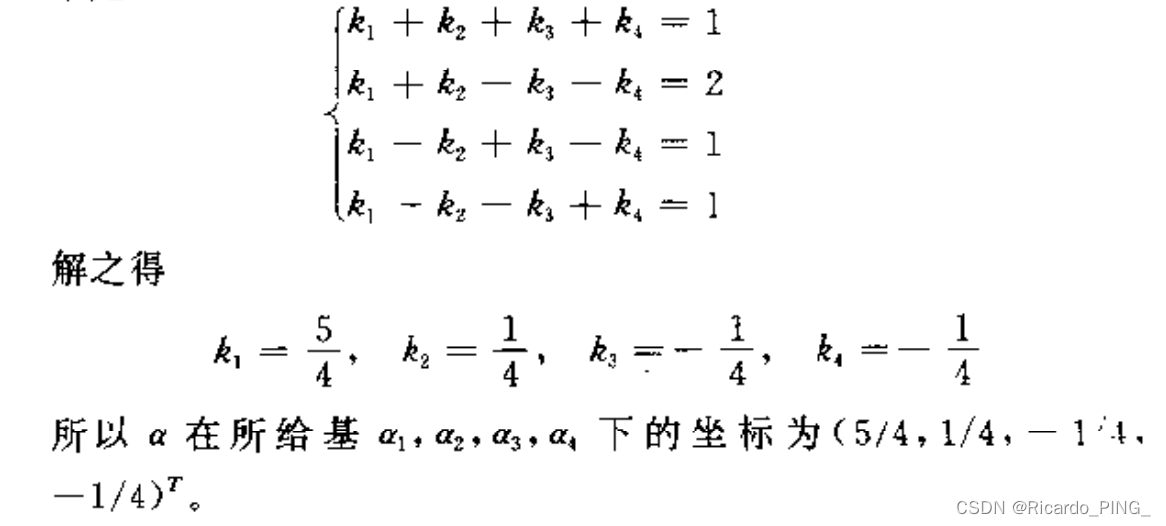
  1.4 基变换和坐标变换

 

 

 

 

 以下给出几组例题

 

这里插入以下逆矩阵的定义和性质 

 

 

 这里链接以下如何求逆矩阵的三种方法

 

 

 

 

 

 

 

 

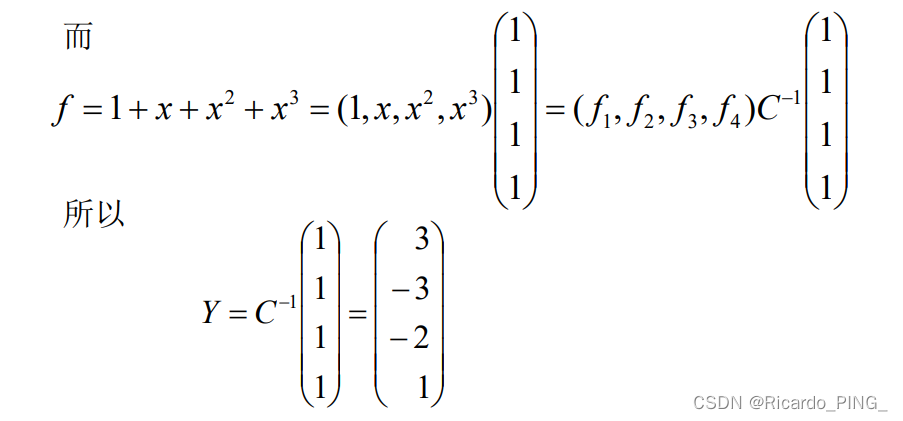
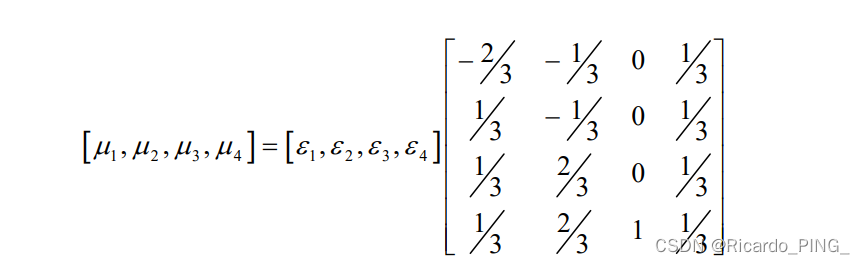
  1.5 线性子空间

 

 

 

 

 

 

充分必要条件

 

 

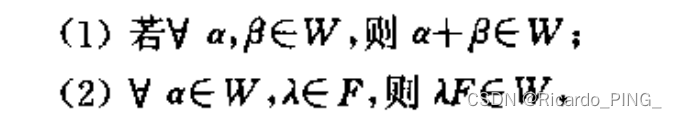
 生成子空间的概念

 

 

 

 

 

 

 1.6 子空间的交与和

 

 

 

 

 

 

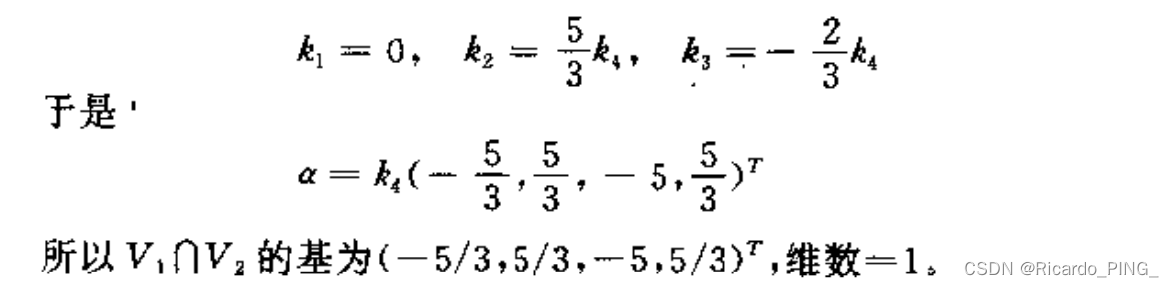
  1.7 子空间的直和

 

 

 

 2. 线性变换

 2.1 线性映射的定义和性质

 

 

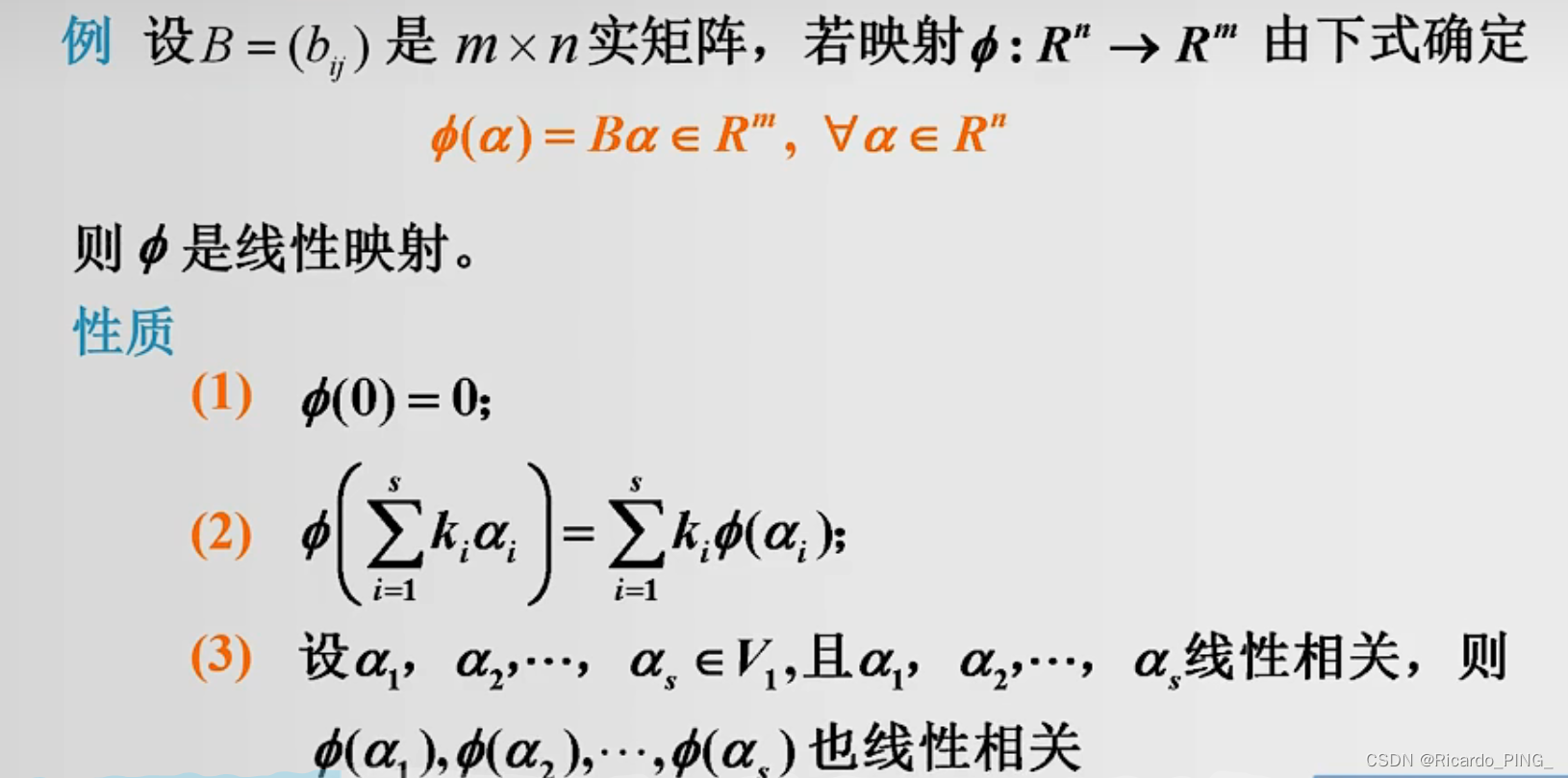
  2.2 线性映射的矩阵表示

 

 

 

 

 

 

 

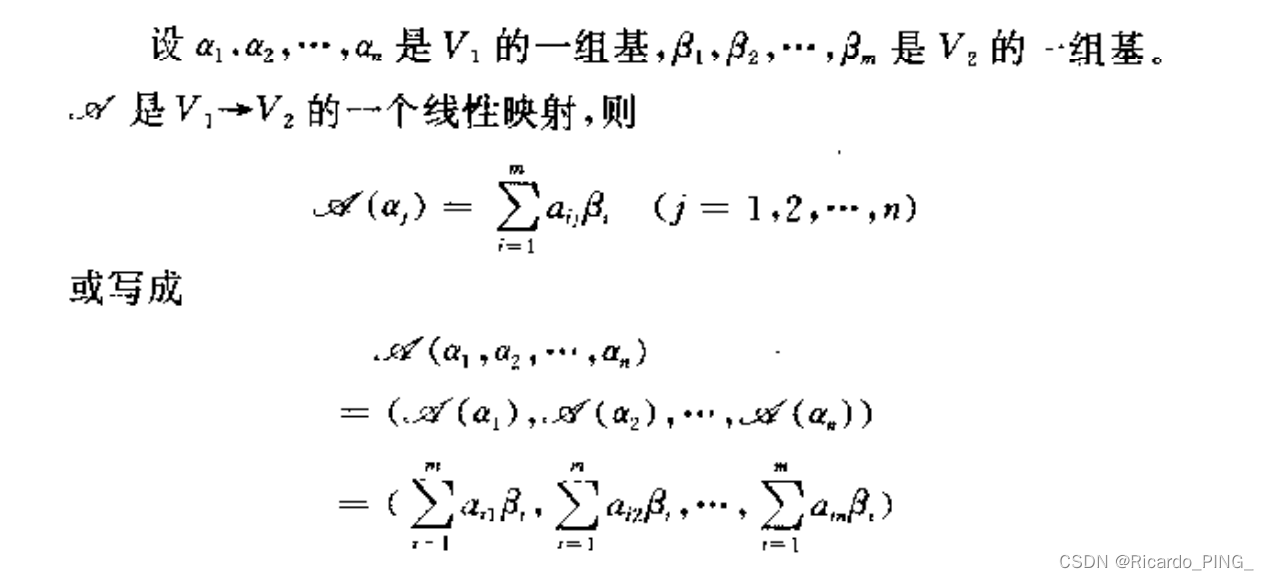
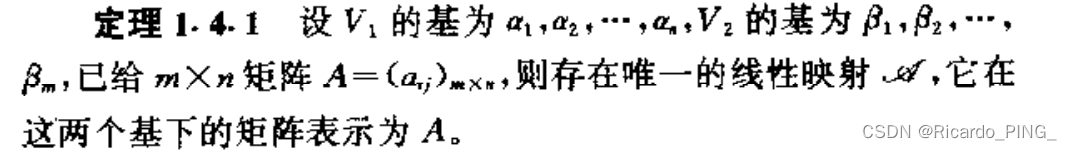
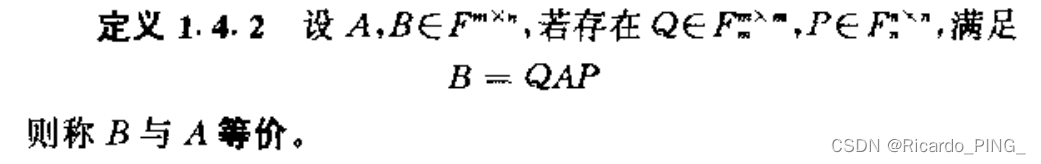
  2.3 线性映射的值域、核子空间

 

 

 

 秩与零度定理

 

  2.4 线性变换的定义和矩阵表示

 

 

    

 

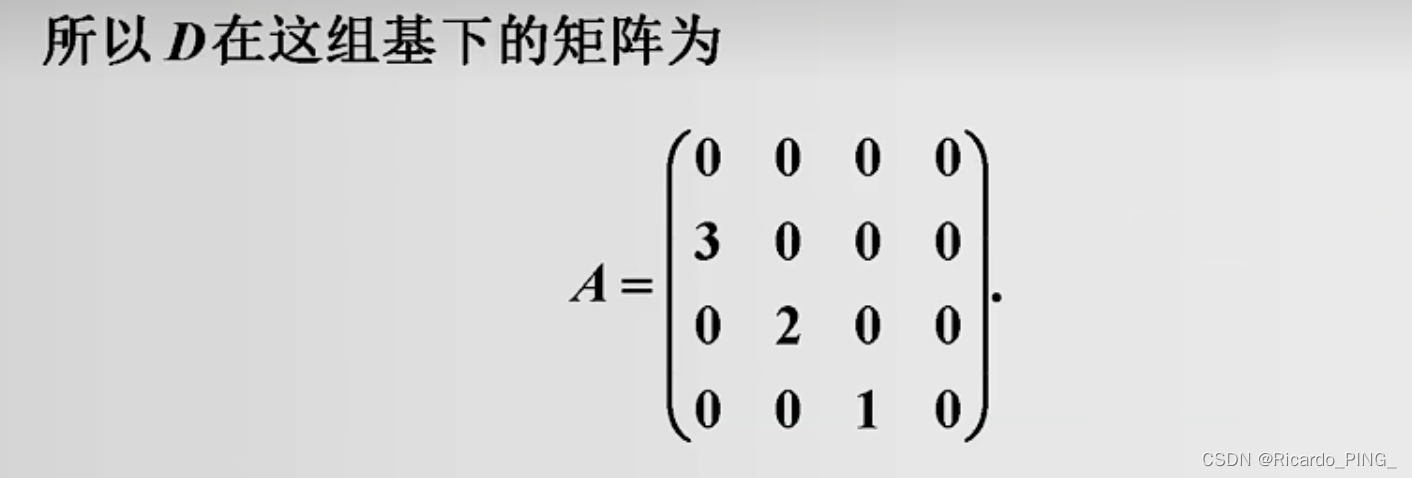
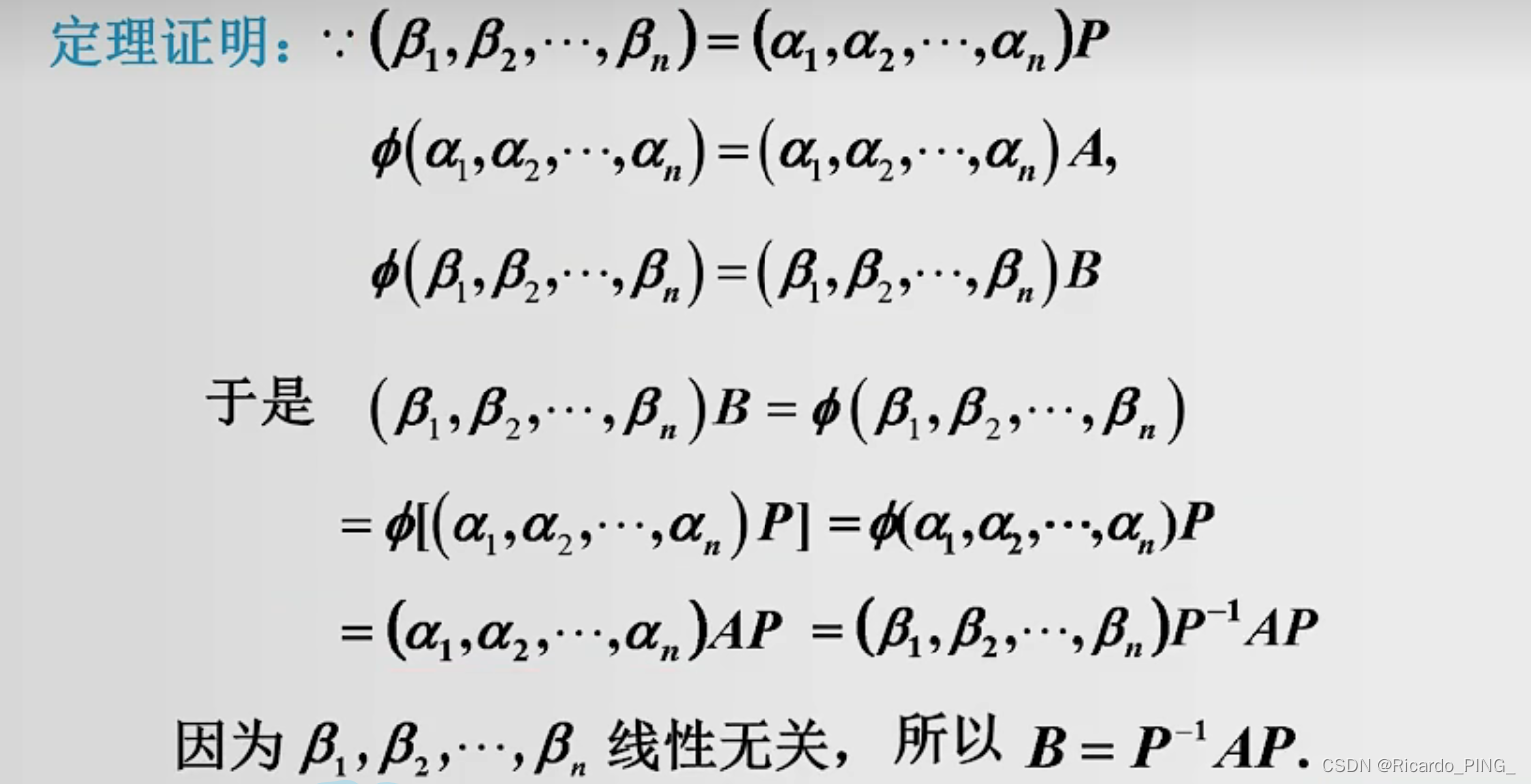
对于上诉知识已经熟知的，可以去看另外一个博主整理完的全部概念，以下放上网址

 线性空间和线性变换