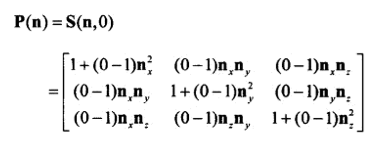本文主要是介绍3D数学基础--矩阵线性变换,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
本章主要讨论用3×3矩阵表达3D线性变换,这个变换不包括平移,包含平移的变换称作仿射变换(就是线性变换后接着平移),需要用4×4矩阵表达。所以本章所讨论的变换都是基于坐标系原点的变换。
旋转
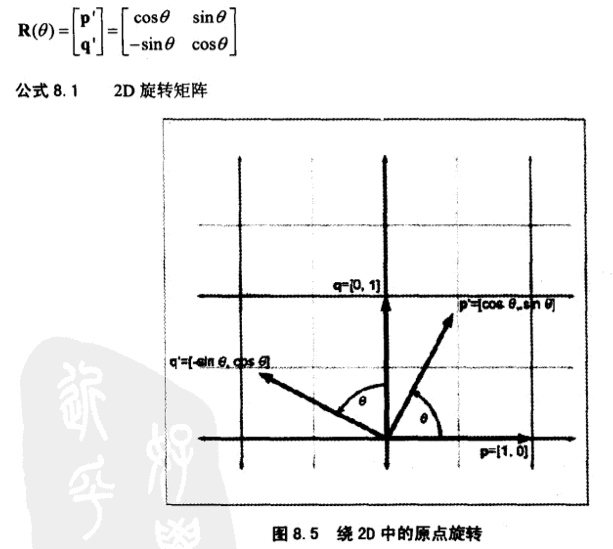
2D中的旋转:因暂不考虑平移,假设物体绕原点旋转,我们通常规定逆时针旋转为正方向,顺时针为负方向(不是必须)。得到的2D旋转矩阵如下图所示:
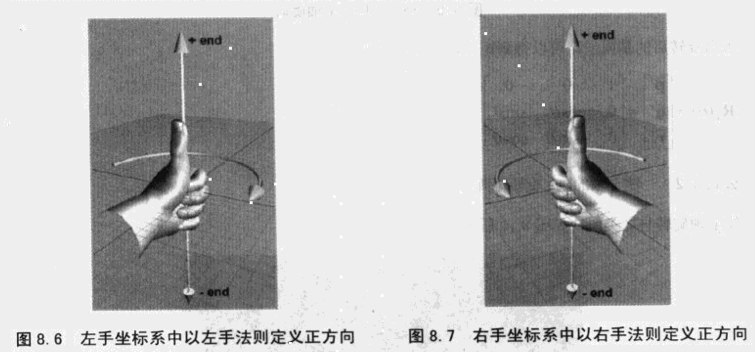
3D中绕坐标轴旋转:同样讨论前需先明确正方向,左手坐标系中定义此方向的规则是左手法则(对应的右手坐标系定义的规则是右手法则),左手法则是:大拇指指向旋转轴的正方向,此时,四指弯曲的方向就是旋转的正方向。如下图所示:
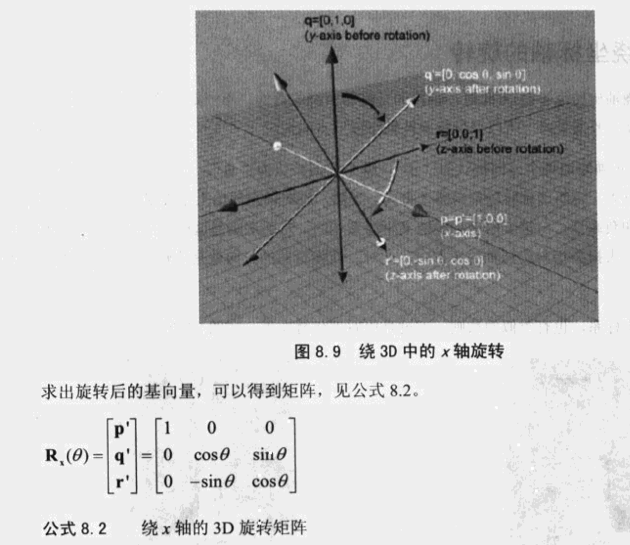
(1)绕x轴旋转:即x轴不变,y,z轴旋转,示意图与公式如下图:
(2)绕y轴旋转:
(3)绕z轴旋转:
3D中绕任意轴旋转:不考虑平移,假定任意轴都穿过原点。用单位向量n描述旋转轴,用θ描述旋转量。公式如下:
缩放
我们可以通过让比例因子k按比例变大或缩小来缩放物体。如果每个轴上的缩放因子都相等,这样的缩放为均匀缩放(等比例缩放),否则为非均匀缩放。
普通缩放
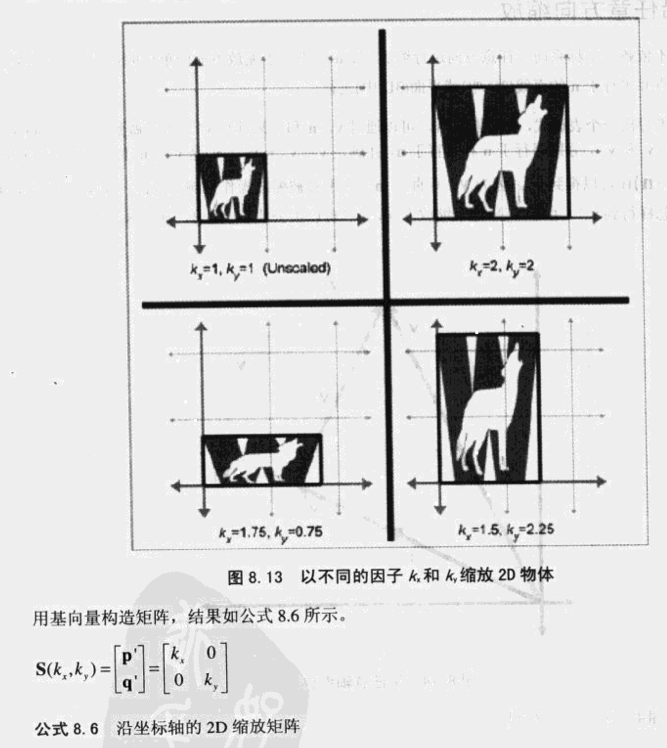
(1)沿坐标轴的2D缩放矩阵示意图与公式如下:
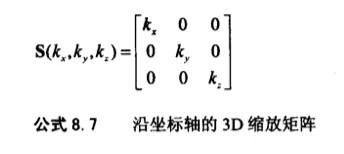
(2)同上,沿坐标轴的3D缩放矩阵公式:
(3)沿任意方向的缩放公式:
特殊缩放
(1)正交投影:投影其实就是降维操作,有一种投影方法是在某个方向上用零作为缩放因子,这种类型的投影称作正交投影。(还有一种透视投影以后讨论)
向坐标轴或平面上投影如下图所示:
向任意直线或平面投影:和前面一样,不考虑平移,这些直线或平面都必须通过原点。投影由垂直于直线或平面的单位向量n定义,注意n垂直于投影直接,不是平行。公式如下:
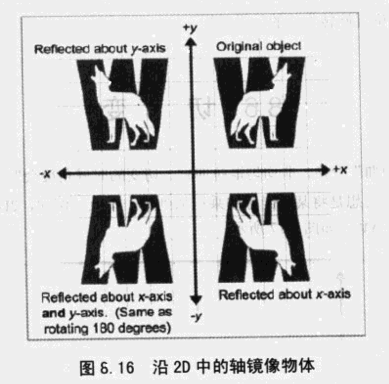
(2)镜像(反射):其表现是将物体沿直线或平面翻折,其实就是设置缩放因子为-1实现的。示意图和公式如下:
(3)切变:是一种坐标系的扭曲变换,非均匀拉伸,角度会发生变化,但面积和体积却保持不变。基本思想是将某一坐标的乘积加到另一个上,例如,2D中,将y乘以某个因子然后加到x上,得到x = x + sy。示意图和公式如下:
变换的组合
乘一个矩阵就等于对应做了某种变换,而矩阵数学计算满足结合律,所以当一个物体要做一系列变换时,可以先将每个矩阵相乘得到一个矩阵,这个新矩阵就代表依次执行原变换的累加效果。这样还能省几次矩阵乘法,从而提高效率。例如:要渲染一个物体,首先要把物体从物体坐标系变换到世界坐标系(M1矩阵),然后再从世界坐标系变换到摄像机坐标系(M2矩阵)。一般我们要分别乘以这两个矩阵,现在我们可以先计算M = M1 × M2,再只要乘以M一个矩阵就可以了。
这篇关于3D数学基础--矩阵线性变换的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!