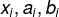求根专题
C++ | Leetcode C++题解之第129题求根节点到叶节点数字之和
题目: 题解: class Solution {public:int sumNumbers(TreeNode* root) {if (root == nullptr) {return 0;}int sum = 0;queue<TreeNode*> nodeQueue;queue<int> numQueue;nodeQueue.push(root);numQueue.push(root->
数学小报4 - 三次方程的求根公式 Quadratic Formula
数学小报4 - 三次方程的求根公式 Quadratic Formula 0. 前言 完整内容同步发表于 https://blog.csdn.net/Mr_Azz/article/details/135443217 由于证明量过于巨大,部分证明简化,详情请见网址。 1. 思考 我们学习过一元二次方程的求根公式 x = − b ± b 2 − 4 a c 2 a x=\frac{-b \p
推导三次以及四次方程的求根公式
三次方程一般形: 令 带入上述方程 省略号标识x的一次以及0次各项.由此可见,含有x^2的项是互相抵消了,所以,任意一个三次方程都可以划归为这种形式: 令 于是有: 无论两数和u+v是怎样的,我们永远可以要求他们的积等于一个预先给定的值,因为如果给定了u+v=A, B=uv,B的值域可以归结为求抛物线方程的值域问
Tomcat内存优化4 求根索源——工具 JVM性能调优监控工具jps、jstack、jmap、jhat、jstat、hprof使用详解
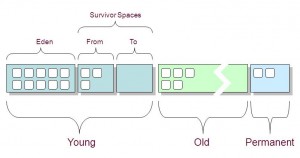
JDK本身提供了很多方便的JVM性能调优监控工具,除了集成式的VisualVM和jConsole外,还有jps、jstack、jmap、jhat、jstat、hprof等小巧的工具,本博客希望能起抛砖引玉之用,让大家能开始对JVM性能调优的常用工具有所了解。 现实企业级Java开发中,有时候我们会碰到下面这些问题: OutOfMemoryError,内存不足 内存泄
Tomcat内存优化4 求根索源——工具 JVM性能调优监控工具jps、jstack、jmap、jhat、jstat、hprof使用详解...
JDK本身提供了很多方便的JVM性能调优监控工具,除了集成式的VisualVM和jConsole外,还有jps、jstack、jmap、jhat、jstat、hprof等小巧的工具,本博客希望能起抛砖引玉之用,让大家能开始对JVM性能调优的常用工具有所了解。 现实企业级Java开发中,有时候我们会碰到下面这些问题: OutOfMemoryError,内存不足 内存泄露
Leetcode: NO.129 求根到叶子节点数字之和 前序遍历
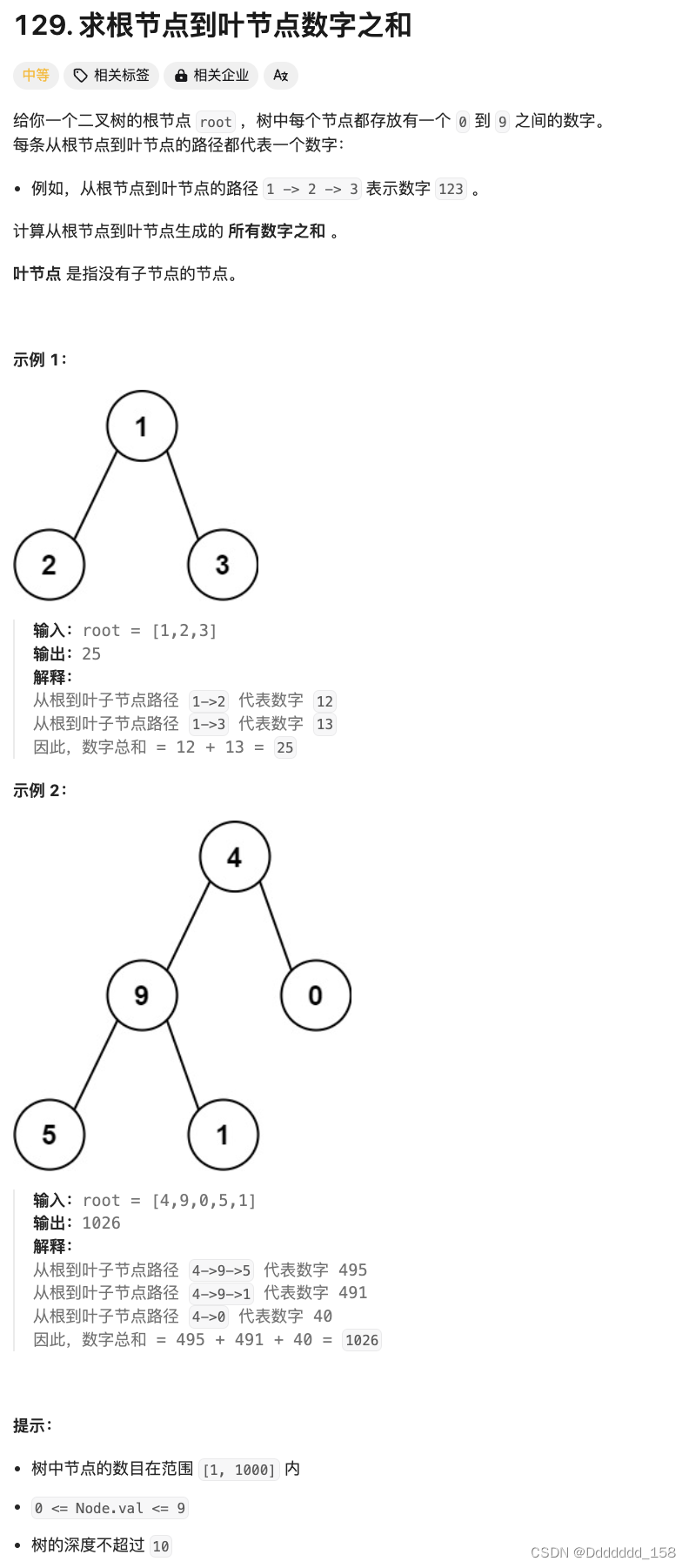
题目 给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。 例如,从根到叶子节点路径 1->2->3 代表数字 123。 计算从根到叶子节点生成的所有数字之和。 说明: 叶子节点是指没有子节点的节点。 示例 1:输入: [1,2,3]1/ \2 3输出: 25解释:从根到叶子节点路径 1->2 代表数字 12.从根到叶子节点路径 1
利用matlab进行多项式求根——符号解
问题描述:对于一个方程,比如: a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0,我们想要求出关于x的表达式(求根)。 如果a,b,c是已知的,或者说是某个确定的数值,那么我们就可以直接用roots函数进行求根——数值解: p=[1 2 1]roots(p) 返回结果是: ans =-1-1 显然这里的a,b,c是未知的,我们想要求出x的表达式—
C语言OJ项目参考(2405)牛顿迭代法求根
2405: 牛顿迭代法求根 Description 用牛顿迭代法求根。方程为 ax3+bx2+cx+d=0 ax^3+bx^2+cx+d=0。系数a,b,c,d的值一次为1,2,3,4,由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。结果保留两位小数。 Input 系数a,b,c,d的值 Output x在1附近的一个实根 Sample Input 1 2 3 4 S
【leetcode热题】求根到叶子节点数字之和
难度: 中等通过率: 40.6%题目链接:. - 力扣(LeetCode) 题目描述 给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。 例如,从根到叶子节点路径 1->2->3 代表数字 123。 计算从根到叶子节点生成的所有数字之和。 说明: 叶子节点是指没有子节点的节点。 示例 1: 输入: [1,2,3]1/ \2 3输出:
二叉树|173. 二叉搜索树迭代器 129. 求根节点到叶节点数字之和
173. 二叉搜索树迭代器 实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器: BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。 boolean hasNex
每日OJ题_二叉树dfs②_力扣129. 求根节点到叶节点数字之和
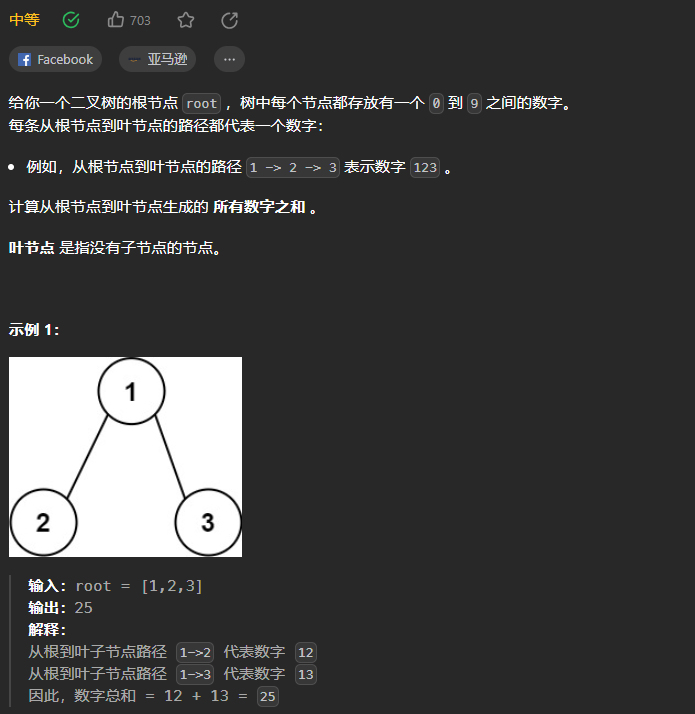
目录 力扣129. 求根节点到叶节点数字之和 解析代码 力扣129. 求根节点到叶节点数字之和 129. 求根节点到叶节点数字之和 难度 中等 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生
【算法设计与分析】求根节点到叶节点数字之和
📝个人主页:五敷有你 🔥系列专栏:算法分析与设计 ⛺️稳中求进,晒太阳 题目 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。 叶节点 是指没有子
128.求根节点到叶节点数字之和
递归yyds class Solution {public int sumNumbers(TreeNode root) {return helper(root,0);}public int helper(TreeNode root,int i){if(root==null) return 0;int temp=i*10+root.val;if(root.left==null&&root.righ
布伦特方法(Brent‘s method)---结合二分法、割线法和逆二次插值法的求根方法
基础介绍: 给定给定区间,函数连续且,那么根据介值定理,函数必然在区间内有根。 二分法:将区间不断二分,使端点不断逼近零点。下一次迭代的区间为或,其中。割线法(线性插值):基本思想是用弦的斜率近似代替目标函数的切线斜率,并用割线与横轴交点的横坐标作为方程式的根的近似。即给定两个点,。其割线方程为,那么令,x的值即为下一次迭代的结果。逆二次插值法:为割线法的进化版本。使用三个点确定一个二次函数,
【转】布伦特方法(Brent‘s method)---求根方法
1. 解方程(Solving Equations) 1.1 二分法(The Bisection Method) 定义1.1 对于方程 ,如果有 ,则说 是 的一个根。 定理1.2 令 是 上的连续函数,满足 , 则 在 和 之间存在一个根。 二分法算法流程: 二分法误差: 在区间 ,
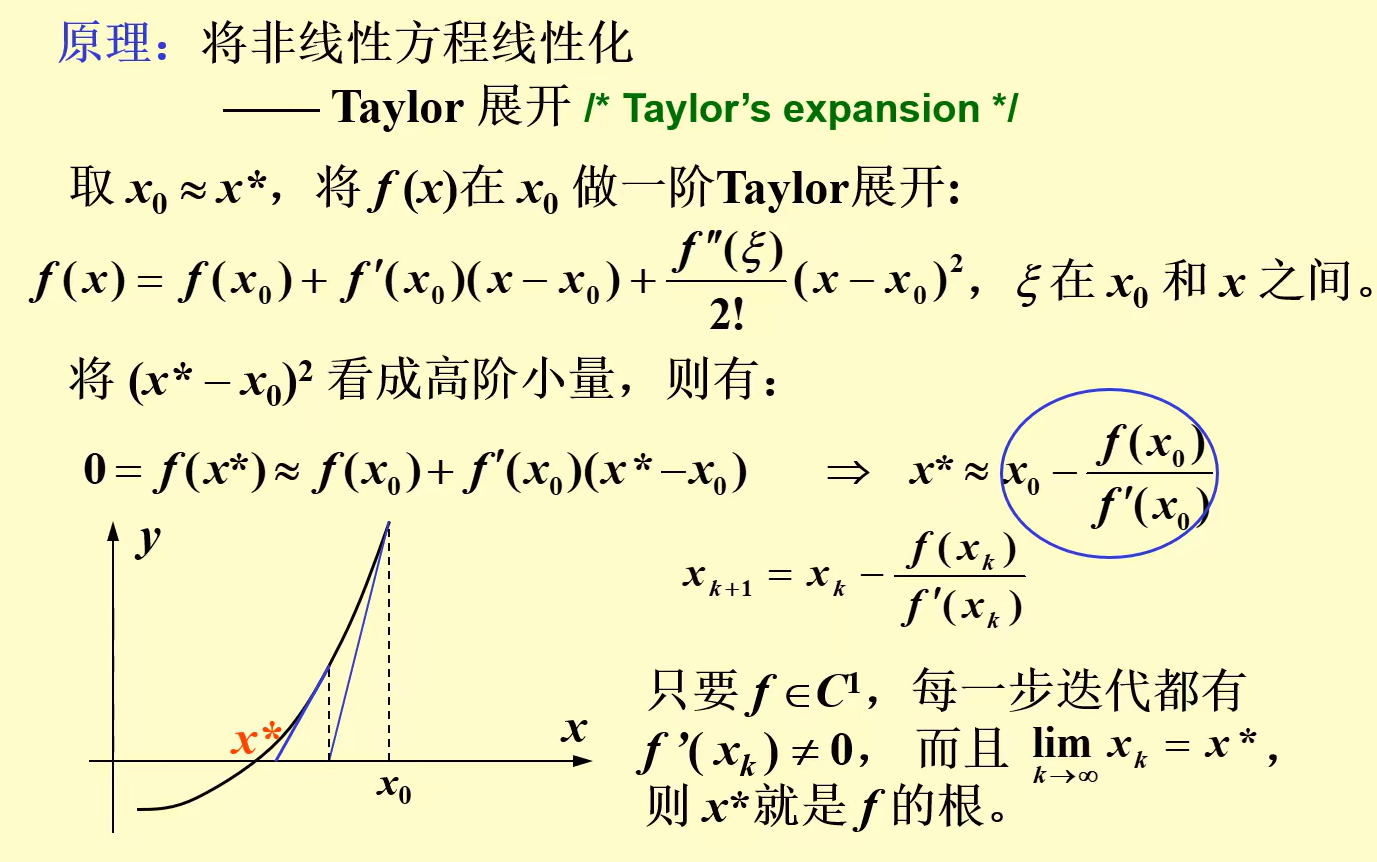
非线性方程求根迭代法(C++)
文章目录 问题描述算法描述不动点迭代法一维情形多维情形 牛顿迭代法单根情形重根情形 割线法抛物线法逆二次插值法 算法实现准备工作一般迭代法割线法抛物线法逆二次插值法 实例分析例1例2 迭代法是一种求解非线性方程根的方法, 它通过构造一个迭代过程, 将一个非线性方程转化为一个等价的不动点方程, 然后通过迭代逼近不动点, 从而得到非线性方程的根. 迭代法的基本思想是将隐式方程转化为
【数值分析】非线性方程求根,二分法,割线法,matlab实现
1. 基本问题 收敛阶 lim k → ∞ ∣ e k + 1 ∣ ∣ e k ∣ r = C > 0 , r 为收敛阶 \lim_{k\to\infty} \frac{|e_{k+1}|}{|e_k|}^r=C>0 \,\,,\,\, r为收敛阶 k→∞lim∣ek∣∣ek+1∣r=C>0,r为收敛阶 2. 二分法 二分法是线性收敛的,如果指定精度 ϵ { \epsilon
leetcode-129. 求根到叶子节点数字之和
题目 给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。 例如,从根到叶子节点路径 1->2->3 代表数字 123。 计算从根到叶子节点生成的所有数字之和。 说明: 叶子节点是指没有子节点的节点。 示例 1: 输入: [1,2,3]1/ \2 3输出: 25解释:从根到叶子节点路径 1->2 代表数字 12.从根到叶子节点路径
迭代法求根 C语言xdoj185
问题描述: 用迭代法求,求平方根的迭代公式为 要求前后两次求出的x的差的绝对值小于。 输入说明: 输入浮点数a。 输出说明: 输出一个浮点数x,小数点后保留5位小数。 输入样例: 3 输出样例: 1.73205 #include <stdio.h>#include <math.h>//迭代法求根int main() {float a;scanf("%f", &a);fl
【LeetCode刷题-树】-- 129.求根节点到叶节点数字之和
129.求根节点到叶节点数字之和 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val;
LeetCode刷题--- 求根节点到叶节点数字之和
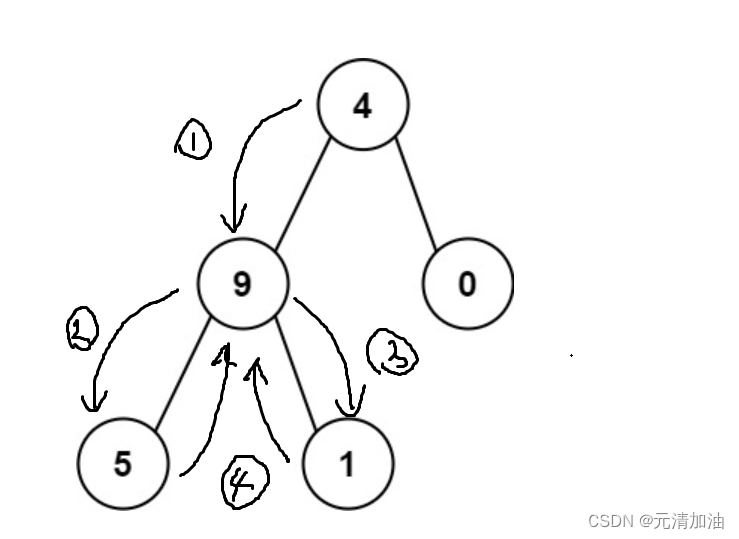
个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏:http://t.csdnimg.cn/ZxuNL http://t.csdnimg.cn/c9twt 前言:这个专栏主要讲述递归递归、搜索与回溯算法,所以下面题目主要也是这些算法做的 我讲述题目会把讲解部分分为3个部分: 1、题目解析 2、算法原理思路讲解
【计算方法】实验一 非线性方程求根数值解法
实验目的 (1)通过对二分法与牛顿迭代法做编程练习和上机运算,进一步体会二分法和牛顿法的不同。 (2)编写割线迭代法的程序,求非线性方程的解,并于牛顿迭代法作比较。 实验内容 1、用牛顿迭代法求下列方程的根 (1) x^2-e^x=0 (2) 〖xe〗^x-1=0 (3) lgx+x-2=0 2、编写割线法程序求解第一问的方程 /* 牛顿迭代法的代码实现* 数值分析* 计科
R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z) 该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) = z 1 + z 2 x + ⋯ + z n x n − 1 p(x)=z_1+z_