【算法设计与分析】求根节点到叶节点数字之和

本文主要是介绍【算法设计与分析】求根节点到叶节点数字之和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

📝个人主页：五敷有你

🔥系列专栏：算法分析与设计

⛺️稳中求进，晒太阳

题目

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例

示例 1：

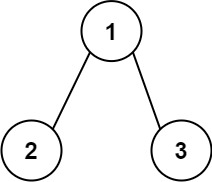
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12从根到叶子节点路径 1->3 代表数字 13因此，数字总和 = 12 + 13 = 25

示例 2：

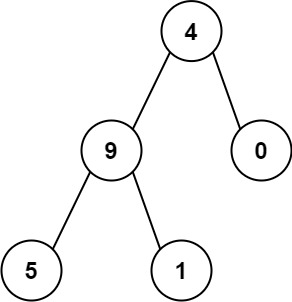
输入：root = [4,9,0,5,1]
输出：1026
解释：从根到叶子节点路径 4->9->5 代表数字 495从根到叶子节点路径 4->9->1 代表数字 491从根到叶子节点路径 4->0 代表数字 40。因此，数字总和 = 495 + 491 + 40 = 1026

思路（递归）

你可以使用深度优先搜索（DFS）来遍历树的所有路径。对于每个节点，你可以递归地计算从根节点到该节点的路径所代表的数字，并将其加到总和中。当遇到叶节点时，将路径所代表的数字加到总和中。

这里我们使用递归来解决这个问题。递归是一种解决问题的方法，其中函数调用自身来解决更小规模的问题。在树的情境下，递归特别适用，因为树的结构本身就是递归定义的。

递归函数的核心思路如下：

基本情况（终止条件）：如果当前节点为空，则返回 0。
计算当前路径所代表的数字：将当前路径的数字计算出来，即将当前的数字乘以 10 再加上当前节点的值。
处理叶子节点：如果当前节点是叶子节点（即没有左右子节点），则返回当前路径所代表的数字。
递归左右子树：对当前节点的左右子树分别调用递归函数，将当前路径所代表的数字传递给它们，并将它们返回的结果相加。
返回结果：将左右子树返回的结果相加，得到从当前节点开始的所有路径所代表的数字之和。

我们就能够递归地计算出从根节点到每个叶子节点的路径所代表的数字之和。

代码实现

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int sumNumbers(TreeNode root) {return sum(root,0);}public int sum(TreeNode root,int i){if(root==null) return 0;int temp=i*10+root.val;if(root.left==null&&root.right==null){return temp;}return sum(root.left,temp)+sum(root.right,temp);}
}