本文主要是介绍非线性方程求根,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.零点定理
函数连续,两端的函数值异号,则存在零点
2.二分法
将有根区间折半,取两端异号的一半区间作为新区间,重复以上操作
误差分析,距离准确解的距离

优点是简单、对函数要求不高,连续即可,缺点是无法求复根及偶重根、收敛慢
3.简单迭代法(不动点迭代)
不同的等效变换:是否收敛、收敛速度不同
4.收敛性
充分条件:压缩映像原理

第一条保证了不动点的存在(想象y=x和y=φ(x)的图像,必有交点)
第二条则保证了不动点的唯一性(想象y=x和y=φ(x)的图像,当φ(x)的导数小于1时,有且仅有1个交点)
误差估计公式
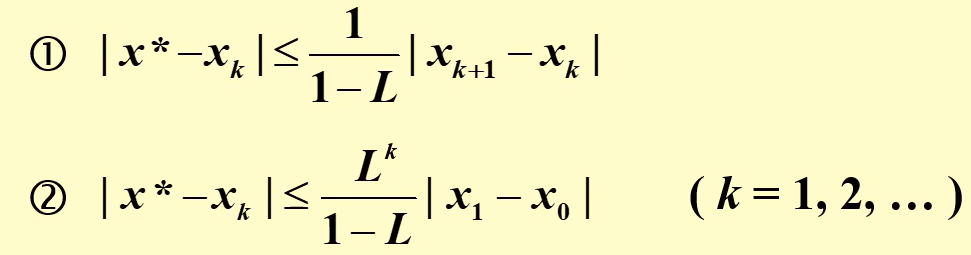
5.局部收敛性定理
x*为φ(x)的不动点,φ‘(x)在x*的某个邻域连续,且|φ‘(x)|<1,则迭代法局部收敛
6.收敛速度
p阶收敛的定义:
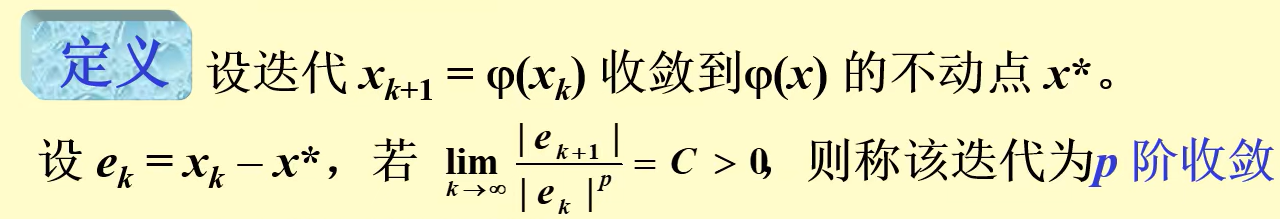
其中C为渐进误差常数,p=1为线性收敛,p=2为平方收敛
收敛阶数的判断条件

7.迭代过程的加速
埃特金(Aitken)算法

斯蒂芬森(steffensen)迭代法(基于埃特金算法)

8.牛顿法
使用某一点的切线代替曲线,求根,求得的根再作为新的点重复上述操作,迭代
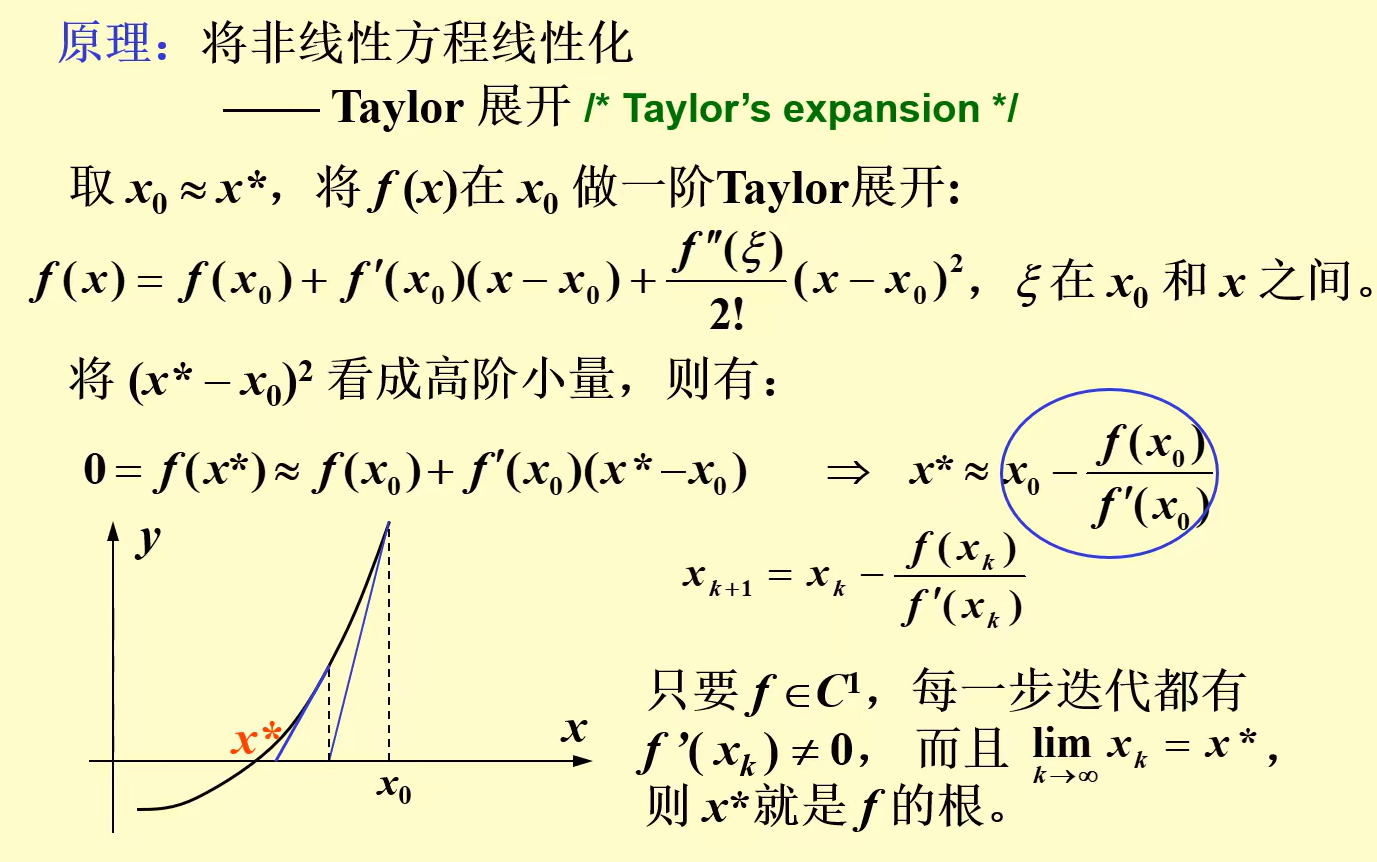
截图源自
【《数值分析》| 华科 | 研究生基础课】https://www.bilibili.com/video/BV1AK4y1k7Px?p=34&vd_source=a53b34e44cbfd40d72a5b337c3e5a13d
这篇关于非线性方程求根的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!