本文主要是介绍推导三次以及四次方程的求根公式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
三次方程一般形:
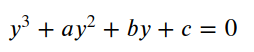
令
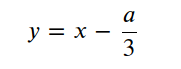
带入上述方程
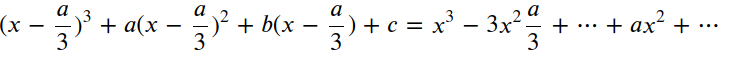
省略号标识x的一次以及0次各项.由此可见,含有x^2的项是互相抵消了,所以,任意一个三次方程都可以划归为这种形式:
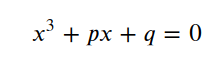
令
![]()
于是有:
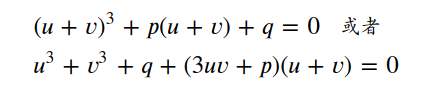
无论两数和u+v是怎样的,我们永远可以要求他们的积等于一个预先给定的值,因为如果给定了u+v=A, B=uv,B的值域可以归结为求抛物线方程的值域问题,或者空间坐标系中抛物线z=xy与x+y=A平面交线z坐标的问题,如下图:

B的任意值,在复数域上u都有对应的解.
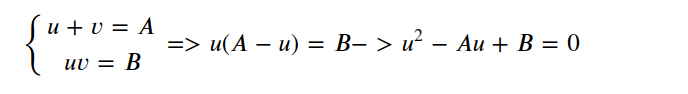
我们可以要求
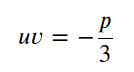
因为这样,可以使得上次不包括u和v的一次项.得到
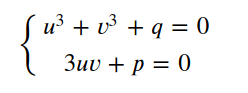
由方程组容易构成以u^3和v^3为根的二次方程.
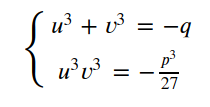
可以得到u^3和v^3是二次方程
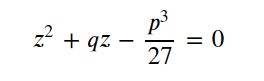
根据二次方程求根公式:

所以:
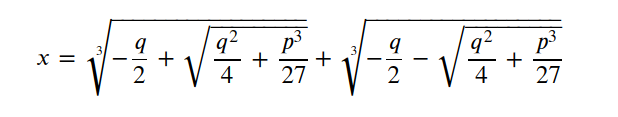
其中:
称为判别式!
即便所有根都为实数根,仍然可能遇到判别式为负数的情况,导致虚数被发现,逐渐收到重视!
三次方程必定有一个实数解,此公式给出的就是这个解,另外两个解可以通过长除法,将三次方程转换为二次方程,求二次方程的虚/实根.
四次方程求根公式推导过程
四次方程的一般式为:
先进行变量替换
则化为下列一般首1的简化四次方程:
法国数学家笛卡尔提出的方法:
分别比较等式两边各项系数,可以得出:
这个经典解法是十六世纪的意大利数学家得到的。
历史上,意大利数学家的这个成就发生了很大影响,在当时,新时代的科学还是第一次超过了旧时代的成就,整个中世纪只是处于了解古代著作的潮流影响之下,而终于在这里解决了古代所不能解决的的问题,这是在新的计算科学,解析几何,微分学以及积分学被发现的一百年的时候,这些新的计算学科最终地肯定了新的科学比旧的优越。
这让我想到了我们的情况,长久以来,包括现在,我们一直都陶醉在古老文明的坟头上不愿离去,所以不乏鼓吹孔老二,中医这样的骗子还在一直活跃。不愿意承认别人的优秀,这样的科研学习环境,是没有希望的。
这篇关于推导三次以及四次方程的求根公式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









