正态分布专题

为什么在很多应用中常采用正态分布/高斯分布、中心极限定理

为什么在很多应用中常采用正态分布/高斯分布？当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎么样的形式时，正态分布是默认的比较好的选择，有两个原因：一，我们想要建模的很多分布的真实情况是比较接近正态分布的。中心极限定理说明很多独立随机变量的和近似服从正态分布。二，在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性。因此，我们可以认为正态分布是对模型加入的

【Tools】什么是正态分布

我们从不正视那个问题那一些是非题总让人伤透脑筋我会期待爱盛开那一个黎明一定会有美丽的爱情 🎵 范玮琪《是非题》正态分布，也称为高斯分布，是统计学中最为常见的一种分布模型。它的概率密度函数可以用一个钟形曲线来描述，呈现出对称的形态。在正态分布中，均值、标准差以及方差是非常重要的参数。正态分布的特点包括：均值（期望值）：正态分布

建模杂谈系列249 增量数据的正态分布拟合

说明从分布开始，分布又要从正态开始假设有一批数据，只有通过在线的方式增量获得。内容 1 生成先通过numpy生成一堆随机数据，从3个正态分布生成，然后拼接起来。 import numpy as npimport matplotlib.pyplot as pltfrom sklearn.mixture import GaussianMixture# 生成示例数据np.

正态分布，泊松分布，指数分布的c/c++代码

https://blog.csdn.net/u012480384/article/details/50838832

什么是正态分布

最重要的连续分布的通用名是概率密度函数，而标准正态分布（Standard Normal Distribution）是最重要的概率密度函数。这个连续分布之所以重要，我认为是因为它非常常见，换句话说，我们会很常用到它。标准正态分布（Standard Normal Distribution）的英文中的normal有正常，通用等意思，也就是说在生活中有很多东西都具有一般的、通用的模式，这个连续分布可以用

PHP实现正态分布的累积概率函数算法

本文转自http://www.cnblogs.com/itsharehome/p/5305671.html 在实际项目中，遇到需要正态分布算法去计算一个数值在整体的分布区间，例如： 100,90,80,70,60,50,40,30,20,10共10个数，按从高到低的顺序排序，总数的10%分布区域为极高频，总数的30%分布区域为高频，总数的40%分布区域为中频，总数的20%分布区域为低频，比如

整型数组处理算法（一）按照正态分布来排列整型数组元素

题目要求如下：给定一个数组input[]，如果数组长度n为奇数，则将数组中最大的元素放到output[]数组最中间的位置，如果数组长度n为偶数，则将数组中最大的元素放到 output[] 数组中间两个位置偏右的那个位置上，然后再按从大到小的顺序，依次在第一个位置的两边，按照一左一右的顺序，依次存放剩下的数。这种处理后结果，如果按照元素的值表示一种分布的图形的话，那绘制后的图形

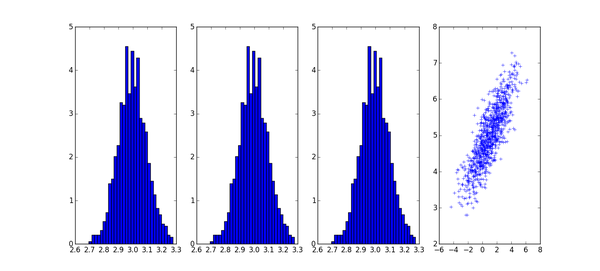
实验七：对比正态分布

2019/04/25 提要对比正太分布的概率密度函数对比正太分布的累计分布函数循环做图情况下，添加图例使用函数：scipy.stats.norm scipy.stats.cdf （本部分代码位于250jupyter根目录下dist_plot 2019/04/25）实验：对比概率密度函数概率密度函数代码使用[2]中。从图中可以看出，标准差越小，整个图显得越尖；

利用均匀分布和中心极限定理产生正态分布（高斯分布）

中心极限定理：设随机变量序列 {Xi} \{X_i\}相互独立，具有相同的期望和方差，即 E(Xi)=μ,D(Xi)=σ

正态分布公式

正态分布（也称为高斯分布）的概率密度函数（PDF）公式如下：对于均值为 (\mu) ，标准差为 (\sigma) 的正态分布，其概率密度函数为： f ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}} f(x)=2πσ2

均匀分布差生正态分布

文章目录中心极限定理中心极限定理中心极限定理是说，n只要越来越大，这n个数的样本均值会趋近于正态分布，并且这个正态分布以u为均值，sigma^2/n为方差。换句话说，假设我们与样本 x 1 , x 2.... x n x1, x2....x_n x1,x2....xn, 并且已经知道 E ( x ) = u , D ( x ) = σ 2 E(x) = u, D(x)

25、matlab随机数生成汇总:控制随机数生成器、均匀分布和正态分布的随机数

python 生成随机一维或多维正态分布

作者：采石工链接：https://www.zhihu.com/question/39823283/answer/115241445来源：知乎著作权归作者所有，转载请联系作者获得授权。# coding=utf-8import numpy as npfrom numpy.linalg import choleskyimport matplotlib.pyplot as plt

高斯分步正态分布

高斯分布，也称为正态分布（Normal Distribution），是统计学和概率论中最重要的分布之一。它由德国数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）首先系统研究并命名。以下是关于高斯分布的详细介绍：高斯分布的定义正态分布是连续概率分布，其概率密度函数（Probability Density Function, PDF）由以下公式给出： f ( x ∣

AI笔记: 数学基础之连续型与均匀分布、指数分布、正态分布等

连续型随机变量及其概率密度 1 ) 连续型随机变量的概念与性质如果对于随机变量X的分布函数F(x)，存在非函数f(x), 使得对于任意实数x, 有 F ( x ) = ∫ − ∞ x f ( t ) d t F(x) = \int_{-\infty}^x f(t)dt

Python检验样本是否服从正态分布

在进行t检验、F检验之前，我们往往要求样本大致服从正态分布，下面介绍两种检验样本是否服从正态分布的方法。 1 可视化我们可以通过将样本可视化，看一下样本的概率密度是否是正态分布来初步判断样本是否服从正态分布。代码如下： import numpy as npimport pandas as pdimport matplotlib.pyplot as plt# 使用pandas和num

Kaiming_normal 正态分布

torch.nn.init.kaiming_normal_(tensor, a=0, mode= 'fan_in', nonlinearity='leaky_relu') 此为0均值的正态分布，N～ (0,std) std = sqrt(2/(1+a^2)*fan_in) a为激活函数的负半轴的斜率，relu是0 mode: 选择“fan_in”保留了forward传递中权重的方差大

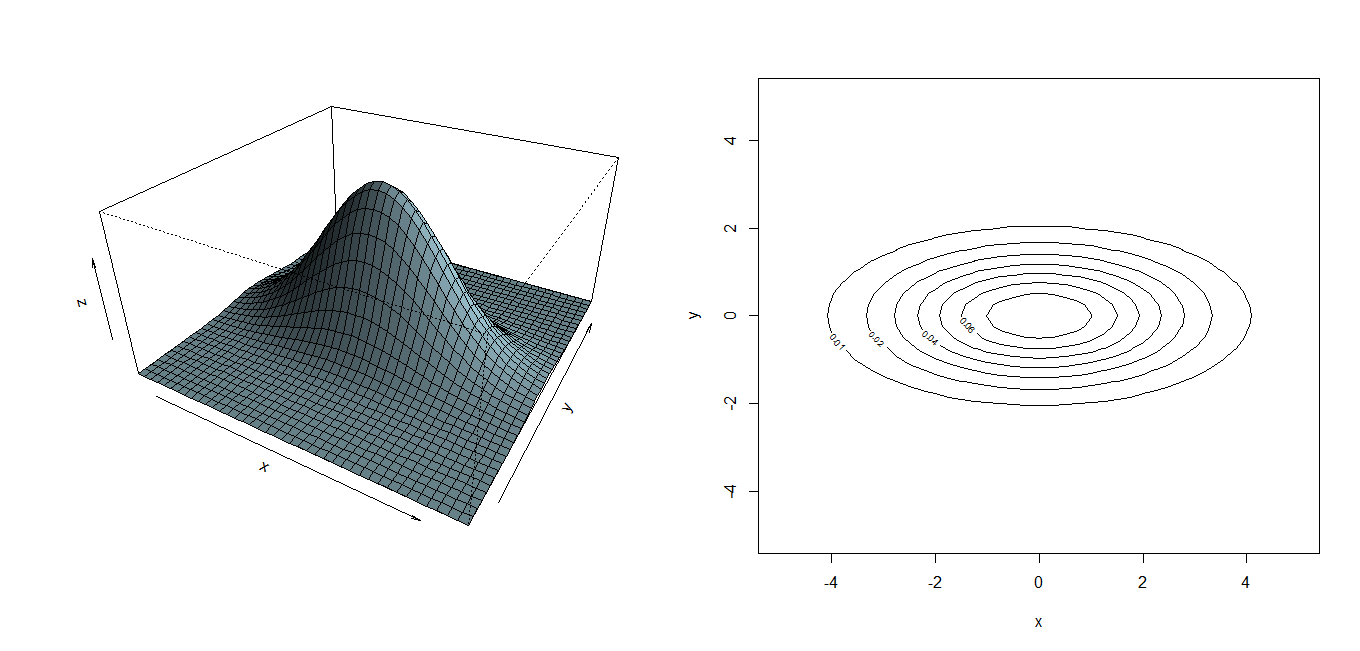
二元正态分布的概率密度函数

二元正态分布随机变量如果随机变量 X X X、 Y Y Y的联合PDF为 p X , Y ( x , y ) = 1 2 π σ x σ Y 1 − p 2 exp ⁡ { − ( x − μ X ) 2 σ X 2 + ( y − μ Y ) 2 σ Y 2 − 2 ρ ( x − μ X ) ( y − μ Y ) σ X σ Y 2 ( 1 − ρ 2 ) } p_{X,Y}(x,y

python 一组数据正态分布散点图_用 Python 检验数据正态分布的几种方法

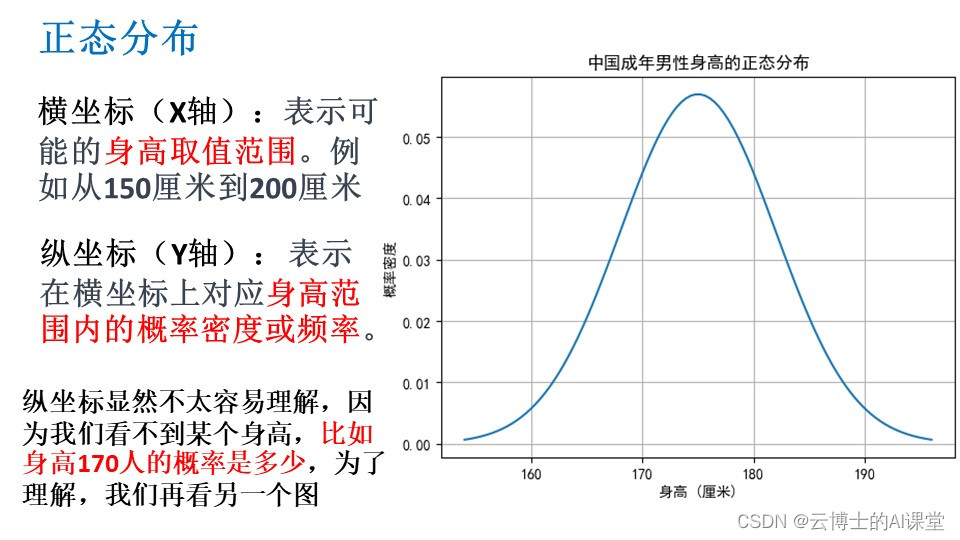
什么是正态分布关于什么是正态分布，早在中学时老师就讲过了。通俗来讲，就是当我们把数据绘制成频率直方图，所构成曲线的波峰位于中间，两边对称，并且随着往两侧延伸逐渐呈下降趋势，这样的曲线就可以说是符合数学上的正态分布。由于任何特征的频率总和都为100%或1，所以该曲线和横轴之间部分的面积也为100%或1，这是正态分布的几何意义。如下图，是数据统计实例中出现的正态分布性数据：为什么要

python对数据列表进行正态分布检验，结果写入excel

最近刚入门python，欢迎大家多多指教！最近接到老师的一个项目，要求对一些医疗数据进行分析现在编写一个allfunction.py函数文件，使得获取excel的数据后，可以对数据进行数据分析。 from xlrd import open_workbookfrom xlutils.copy import copyimport xlrdimport xlwtfrom pandas.c

学界 | 为什么数据科学家都钟情于最常见的正态分布？

对于深度学习和机器学习工程师们来说，正态分布是世界上所有概率模型中最重要的一个。即使你没有参与过任何人工智能项目，也一定遇到过高斯模型，今天就让我们来看看高斯过程为什么这么受欢迎。高斯分布（Gaussian distribution），也称正态分布，最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一

正态分布-形状与特点

更多AI技术入门知识与工具使用请看下面链接： https://student-api.iyincaishijiao.com/t/iNSVmUE8/

[C++] 使用＜random＞头文件生成均匀分布、正态分布的数据

一、摘要对于满足指定分布的自由变量，如果无法通过分布函数公式计算得到其期望和方差，可以考虑使用采样法得到其期望、方差值的近似值。在此过程中需要按照特定的分布函数进行随机采样，并统计采样数据，可以使用蒙特卡洛或者接受拒接方法得到满足特定分布的随机变量。本文简要介绍了如何使用C++random头文件中自带的函数得到满足均匀分布和高斯分布的变量。二、代码 0. c++中随机数生成的基本

二元正态分布

事隔两天再看这里写的东西,发现自己的理解偏差太多,太无知,这里的东西尤其那些不是转帖来的内容,自己凭当时一知半解当做学习笔记自娱自乐而已;如果有人要参考,请自己慎重斟酌,这里的问题和错误我一般不修改. 介绍二元联合正态分布的东西,通常教材就不多见. Wolfram的这个材料非常漂亮,参考文献也详细,值得一读: http://mathworld.wolfram.com/BivariateNor

正态分布？

全是个人理解正态分布是一种广泛出现的连续概率分布，比如身高，分数二项分布是离散情况下的概率分布比如仍硬币，正面的可能性是 p p p，那么仍 n n n 次， x x x 次正面的概率为 ( n x ) p x ( 1 − p ) n − x \binom nxp^x(1-p)^{n-x} (xn)px(1−p)n−x 容易得到均值 μ = n p \mu=np μ=np，方差

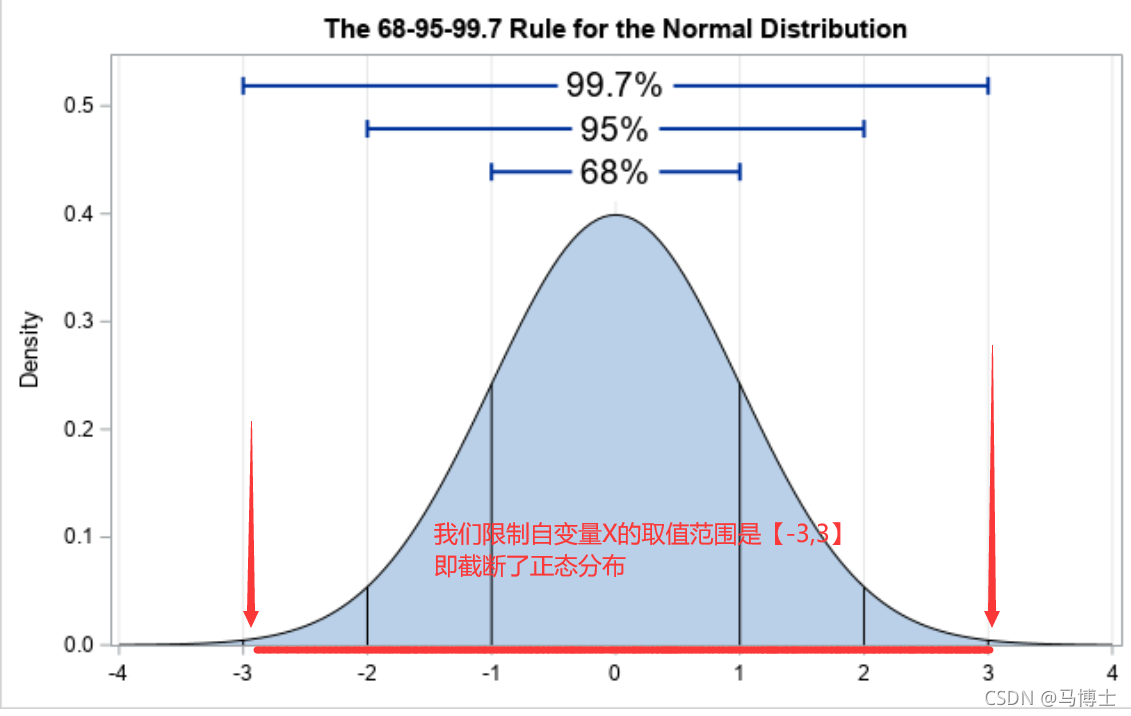
截断正态分布（Truncated normal distribution）nn.init.trunc_normal_()

截断正态分布概念： Normal Distribution 称为正态分布，也称为高斯分布，Truncated Normal Distribution一般翻译为截断正态分布，也有称为截尾正态分布。截断正态分布是截断分布(Truncated Distribution)的一种，那么截断分布是什么？截断分布是指，限制变量xx 取值范围(scope)的一种分布。例如，限制x取值在0到50之间，即{0<