截断正态分布（Truncated normal distribution）nn.init.trunc_normal_()

截断正态分布概念：

Normal Distribution 称为正态分布，也称为高斯分布，Truncated Normal Distribution一般翻译为截断正态分布，也有称为截尾正态分布。

截断正态分布是截断分布(Truncated Distribution)的一种，那么截断分布是什么？截断分布是指，限制变量xx 取值范围(scope)的一种分布。例如，限制x取值在0到50之间，即{0<x<50}。因此，根据限制条件的不同，截断分布可以分为：

1. 限制取值上限，例如，负无穷<x<50
2. 限制取值下限，例如，0<x<正无穷
3. 限下限取值都限制，例如，0<x<50

正态分布则可视为不进行任何截断的截断正态分布，也即自变量的取值为负无穷到正无穷；例如下图，我们将正态分布的变量范围限制在【-3,3】内，那么我们就说我们截断了正态分布

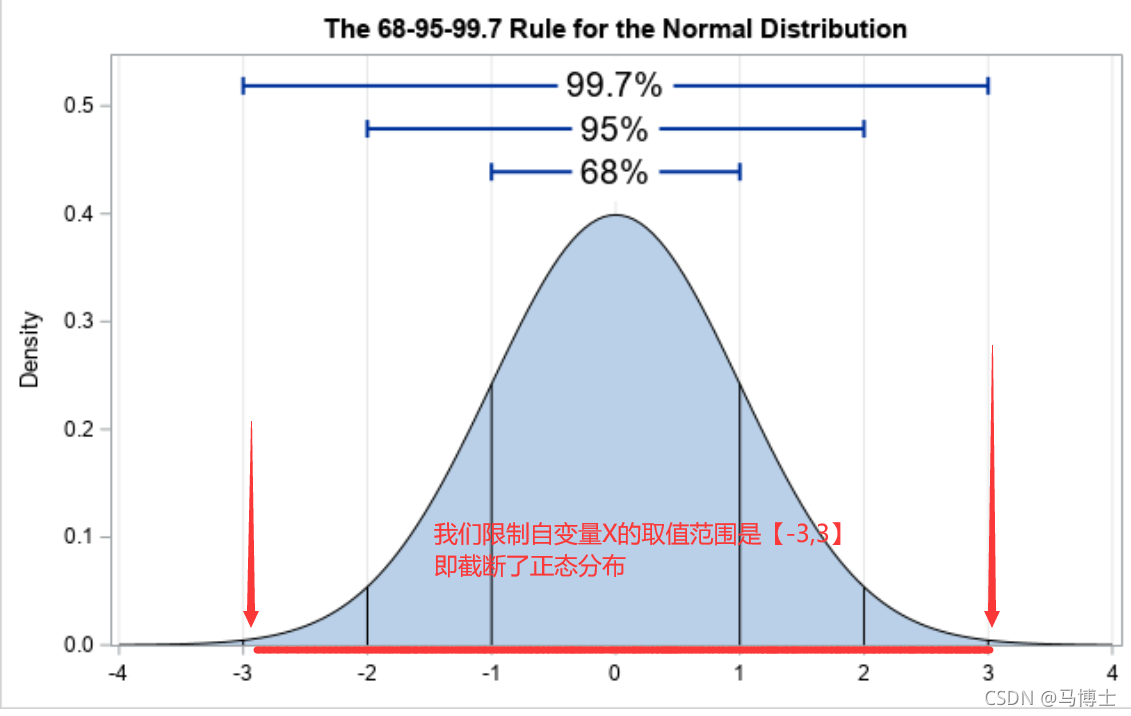
想要截断范围的正态分布的意图

1. 限制变量的取值范围：截断正态分布可以限制变量的取值范围，以使得分布更符合实际情况。在某些领域中，如金融领域中的股票价格，截断正态分布可以更好地描述实际情况，因为它将对变量的最大值和最小值进行限制。

2. 减少异常值的影响：在实际数据中，存在一些极端值或异常值，这些值可能会对分析结果产生不良影响。通过截断正态分布，可以将这些异常值排除在分布范围之外，从而减少它们对分析结果的影响。

3. 更好的模型拟合：在某些情况下，正态分布可能不能很好地拟合实际数据。通过截断正态分布，可以改善模型的拟合效果，提高拟合的准确性。【例如：想要去拟合数据，根据观察原始数据分布在1的左右，在使用GAN生成数据的时候发现拟合不到，那么猜想可能是我生成虚假数据的时候范围有问题，所以想要限制范围的正态分布】

4. 更好的推断和预测：截断正态分布可以提高推断和预测的精度。在一些应用中，如概率统计、机器学习等领域，截断正态分布被广泛应用于数据建模和预测中。

截断了的正态分布还有正态的意义吗？

截断了的正态分布仍然有正态分布的意义。截断是指对正态分布进行了限制，使其只在某个区间内有定义。这种截断可能是单侧的或双侧的。截断的目的是限制变量的取值范围，以使得分布更符合实际情况。

截断了的正态分布仍然保留着正态分布的许多特征，比如它的均值、方差、标准差等。截断的影响主要表现在分布的尾部，即截断的区间之外。截断会使得分布在截断区间之外的概率变小，而在截断区间内的概率变大。

使用（可以规定正态分布的范围，均值，标准差...）

def trunc_normal_(tensor: Tensor, mean: float = 0., std: float = 1., a: float = -2., b: float = 2.) -> Tensor:

Args:tensor: an n-dimensional `torch.Tensor`mean: the mean of the normal distributionstd: the standard deviation of the normal distributiona: the minimum cutoff valueb: the maximum cutoff valueExamples:>>> w = torch.empty(3, 5)>>> nn.init.trunc_normal_(w)
"""