二元正态分布

本文主要是介绍二元正态分布，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

事隔两天再看这里写的东西,发现自己的理解偏差太多,太无知,这里的东西尤其那些不是转帖来的内容,自己凭当时一知半解当做学习笔记自娱自乐而已;如果有人要参考,请自己慎重斟酌,这里的问题和错误我一般不修改.

介绍二元联合正态分布的东西,通常教材就不多见.

Wolfram的这个材料非常漂亮,参考文献也详细,值得一读:
http://mathworld.wolfram.com/BivariateNormalDistribution.html

田纳西理工大学(Mathematics Department, Motoya Machida 2006, Tennessee Technological University)的这个Interactive Statistics with R 讲义材料也不错(有一小段提到, 作者Motoya Machida似乎是日裔学者); 这个材料的网页版 其网页版

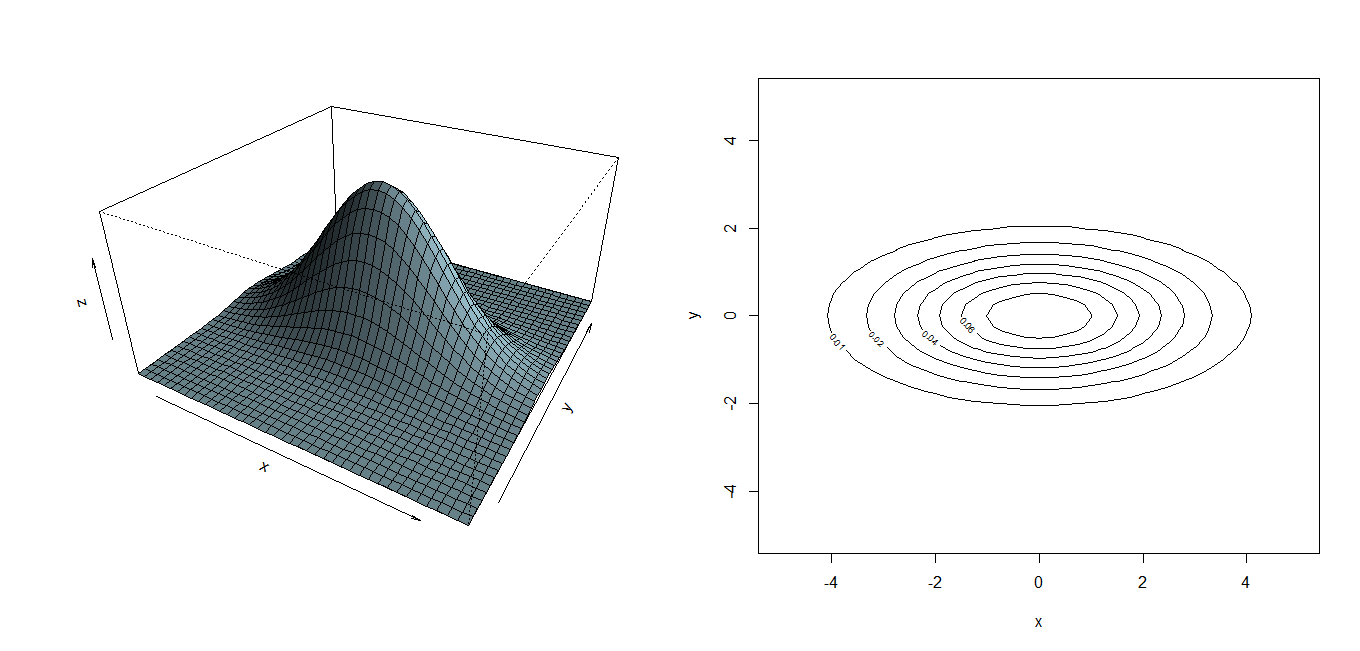
下面的根据协方差矩阵绘制二维联合概率密度图像的R语言代码来自另一所大学的讲义:

library(mvtnorm) 
sigma.xx<-4 
sigma.yy<-1 
sigma.xy<-0 
sigma<-matrix(c(sigma.xx,sigma.xy,sigma.xy,sigma.yy),ncol=2) 
old.par<-par(mfrow=c(1,2)) 
x<-seq(-5,5,by=0.25) 
y<-x 
f<-function(x,y){ 
+ xy<-cbind(x,y) 
+ dmvnorm(xy,c(0,0),sigma) 
+ } 
z<-outer(x,y,f) 
persp(x,y,z,theta=30,phi=30,expand=0.5,col=”lightblue”,ltheta=120,shade=0.75)
contour(x,y,z,method=”edge”,xlab=”x”,ylab=”y”) 
par(old.par)

library(mvtnorm)
sigma.xx<-4
sigma.yy<-1
sigma.xy<-0
sigma<-matrix(c(sigma.xx,sigma.xy,sigma.xy,sigma.yy),ncol=2)
old.par<-par(mfrow=c(1,2))
x<-seq(-5,5,by=0.25)
y<-x
f<-function(x,y){
+ xy<-cbind(x,y)
+ dmvnorm(xy,c(0,0),sigma)
+ }
z<-outer(x,y,f)
persp(x,y,z,theta=30,phi=30,expand=0.5,col=”lightblue”,ltheta=120,shade=0.75)
contour(x,y,z,method=”edge”,xlab=”x”,ylab=”y”)
par(old.par)

这篇关于二元正态分布的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---