正交专题
【线性代数】【二】2.10 标准正交基与正交矩阵
文章目录 前言一、标准正交基二、施密特正交化三、 正交矩阵总结 前言 本文将介绍正交基、正交矩阵、与施密特正交化算法。正交是向量中一种非常好的性质,意味着两个向量互相之间没有冗余,也容易被区分。 一、标准正交基 前面我们学习过,一个向量空间的基是指张成该空间的极大线性无关组。例如 [ 1 , 0 , 0 ] , [ 1 , 1 , 0 ] , [ 1 , 1 , 1
【因果推断python】51_去偏/正交机器学习3
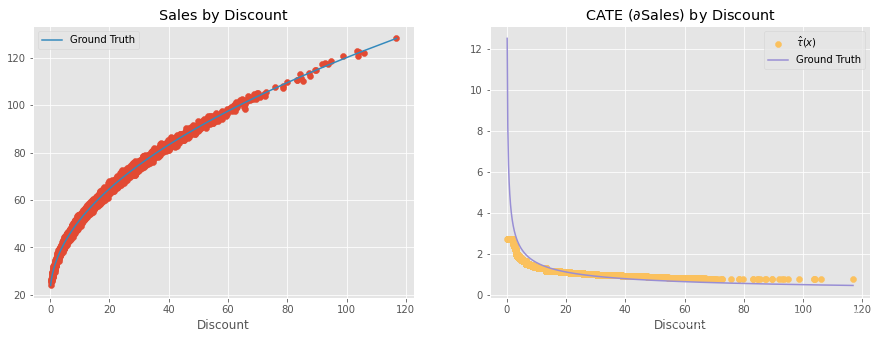
目录 What is Non-Parametric About? What is Non-Parametric About? 在我们继续之前,我只想强调一个常见的误解。当我们考虑使用非参数 Double-ML 模型来估计 CATE 时,我们似乎会得到一个非线性治疗效果。例如,让我们假设一个非常简单的数据生成过程(DGP),其中 discont 对销售额的影响是非线性的,但却是通过
测试基础14:测试用例设计方法-正交实验法
课程大纲 1、定义 正交表是一种在数学和统计学中使用的特殊表格,用于设计实验,以在有限的测试次数下获得最大的测试覆盖率。 它通过均衡搭配的特性,从全面试验中挑选出有代表性的点进行测试。 2、应用场景 适用于配置类软件中组合比较多的情况。与判定表对比,输出结果不复杂,不会因组合不同有非常大差异。(如:多个单选下拉框、选项多的单选框组合
Matlab解决施密特正交规范化矩阵(代码开源)
#最近在学习matlab,刚好和线代论文重合了 于是心血来潮用matlab建了一个模型来解决施密特正交规范化矩阵。 我们知道这个正交化矩阵挺公式化的,一般公式化的内容我们都可以用计算机来进行操作,节约我们人工的时间。 我们首先把矩阵导入进去,之后计算投影的长度进行缩减。进行正交化 之后单独进行规范化 代码如下: %%% 施密特正交化a=ones(3,3); % 假设3行,3列
CGS与MGS的矩阵正交化-C语言实现
格拉姆-施密特正交化和改进的格拉姆-施密特正交化 格拉姆-施密特正交化CGS 数学公式 代码实现: 过程版 矩阵运算实现的难点在于每次运算都是一个向量,需要for循环进行,会带来运算时在代码中的复杂,进而难以理解代码的过程 Q矩阵是{e...} R矩阵是上三角矩阵 Q[0] = A[0]; // -> b1 = a1R[0][0] = norm(Q[0], m)
线性代数|机器学习-P4正交矩阵中的标准正交向量
文章目录 1. 正交矩阵Q1.1 矩阵Q的推导1.2 |Qx|=|x| 2. 常见正交矩阵2.1 旋转矩阵2.2 镜像矩阵2.3 Householder矩阵2.4 Hadamard矩阵2.4 小波矩阵2.5 傅里叶级数矩阵 1. 正交矩阵Q 1.1 矩阵Q的推导 方阵A正交的充要条件是A的行(列)向量组是单位正交向量组. 我们定义正交矩阵Q表示如下: Q = [ q 1 q
科研软件 | 正交设计助手 安装教程
软件介绍 正交设计助手是一个十分强大的实验室校验工具,正交设计助手使用起来非常的简单,正交设计助手是一款针对正交实验设计及实验结果的分析而制作的专业软件。正交设计方法是我们常用的实验设计方法,它让我们以较少的实验次数得到科学的实验结论。 安装步骤 1、双击解压 2、进入解压后文件 3、双击运行 4、软件安装完成 软件下载 https://docs.q
稀疏表示学习笔记--正交阵,协方差
自己的数学基础比较差,特别是矩阵一块,有一些名词看到了可能不能立刻反应出是什么意思,所以在这里进行一些记录。 1、正交矩阵 如果:AA T=E(E为单位矩阵,A T表示“矩阵A的转置矩阵”。)或A TA=E,则n阶 实矩阵A称为正交矩阵, 若A为 正交阵,则满足以下条件: 1) A T是正交矩阵 2) (E为单位矩阵) 3) A的各行是单位向量且两两正交 4) A
正交频分复用回顾(通俗易懂)
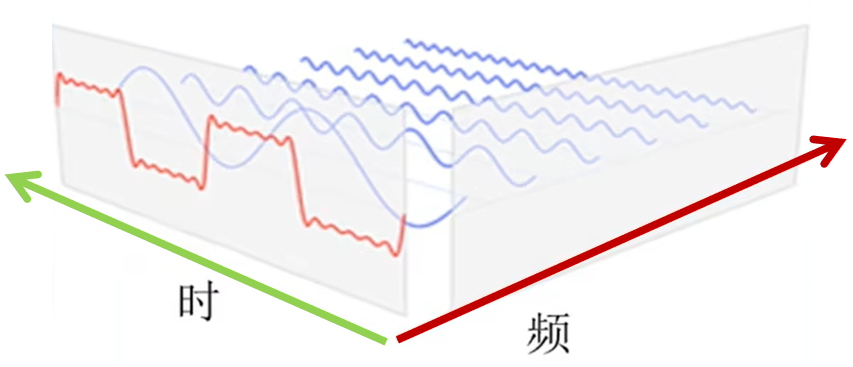
OFDM我们知道,叫做正交频分复用,它是4G的一个关键技术,4G的多址技术叫做OFDMA,也就是说4G是通过OFDM来作用户区分的,具体是什么意思呢?继续往下看。 图1 在2G和3G时代, 单用户都是用的一个载波,也就是单载波,图1中的横轴代表频率,纵轴代表强度。那进入4G时代之后,我们开始使用多个子载波,来进行多个信息的并行传输,如图1右下角所示,就是多个子载波同时传输的示意图。 我
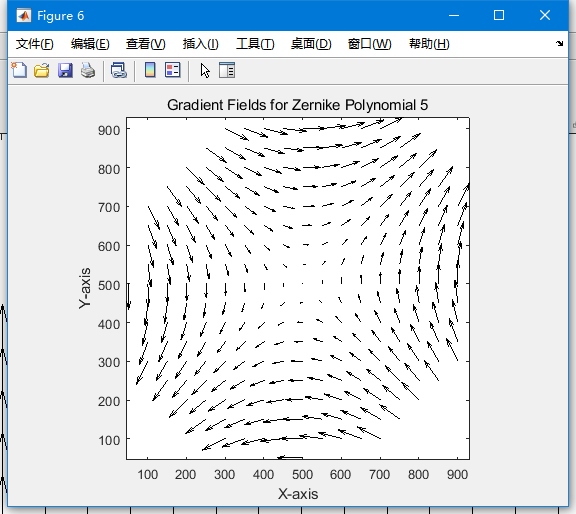
单位圆内的正交向量多项式,第一部分:由Zernike多项式的梯度导出的基组
clear all;close all;clc;%%I1=double(imread('E:\zhenlmailcom-E8E745\华为家庭存\image\imgs\right\0.bmp'));I2=double(imread('E:\zhenlmailcom-E8E745\华为家庭存储\.法\image\imgs\right\1.bmp'));I3=double(imr
现代计算机图形学笔记(二)——三维变换、正交透视投影
三维变换 和上节一样,我们使用齐次坐标 3D点: ( x , y , z , 1 ) ⊤ (x,y,z,1)^\top (x,y,z,1)⊤3D向量: ( x , y , z , 0 ) ⊤ (x,y,z,0)^\top (x,y,z,0)⊤ 通常情况下, w ≠ 0 w\neq0 w=0,3D点表示为 ( x / w , y / w , z / w , 1 ) ⊤ (x/w,y/w,
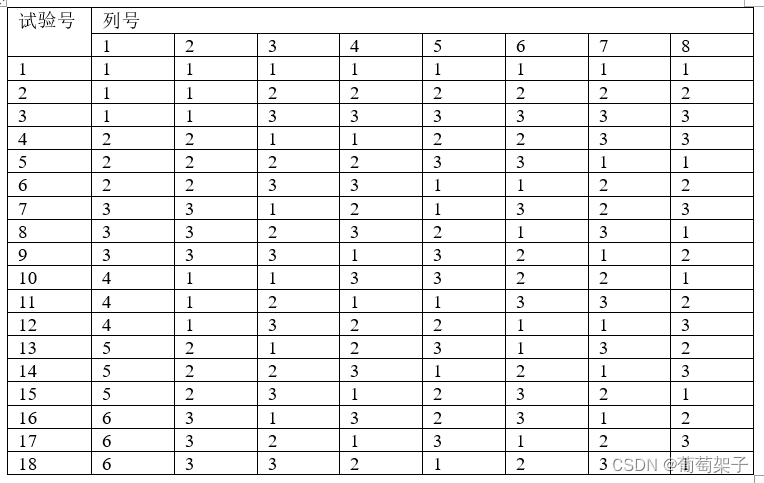
软件测试_正交表使用方法
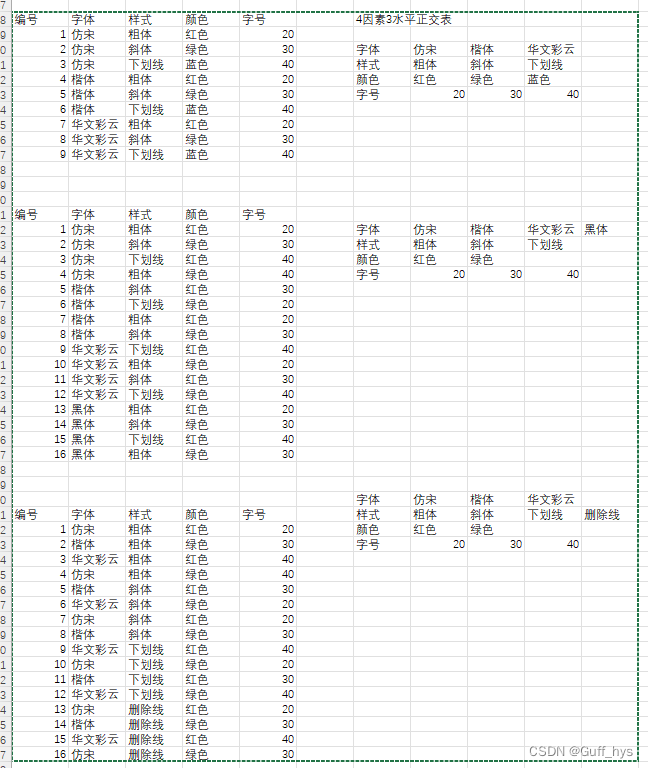
编号字体样式颜色字号4因素3水平正交表1仿宋粗体红色202仿宋斜体绿色30字体仿宋楷体华文彩云3仿宋下划线蓝色40样式粗体斜体下划线4楷体粗体红色20颜色红色绿色蓝色5楷体斜体绿色30字号2030406楷体下划线蓝色407华文彩云粗体红色208华文彩云斜体绿色309华文彩云下划线蓝色40编号字体样式颜色字号1仿宋粗体红色20字体仿宋楷体华文彩云黑体2仿宋斜体绿色30样式粗体斜体下划线3仿
多因素不同水平的正交表设计(并列法)
文章目录 一、问题提出二、举例说明 一、问题提出 参考高等教育课本《实验设计与数据处理》 很多时候,我们要考察的因素水平数不尽相同,这时候一般采用混合水平正交表或者对普通的正交表作修改,其中,混合水平正交表由于水平数不规则,不能进行交互作用设计,针对不同水平的复杂特性,我们可以对标准正交表进行改造,下面以实例介绍一种并列法; 二、举例说明 在Vc二步发酵的配方实验中,有七个影
Sweet Snippet 之 Gram-Schmidt 正交化
Gram-Schmidt 正交化的简单实现 Gram-Schmidt(格拉姆-施密特) 正交化可以正交化一组给定的向量,使这些向量两两垂直,这里列出一份简单的实现(Lua): -- vector addfunction add(a, b)if a and b and #a == #b thenlocal ret = {}for i = 1, #a dotable.insert(ret,
【图像加密】基于matlab GUI正交拉丁方置乱算法图像加解密【含Matlab源码 182期】
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。 🍎个人主页:海神之光 🏆代码获取方式: 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭:行百里者,半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理(进阶版) 路径规划(Matlab) 神经网络预测与分类(Matlab) 优化求解(Matlab) 语音处理(Matlab
【图像加密】基于matlab GUI正交拉丁方置乱+混沌图像加密解密【含Matlab源码 636期】
⛄一、获取代码方式 获取代码方式1: 完整代码已上传我的资源:【图像加密】基于matlab GUI正交拉丁方置乱+混沌图像加密解密【含Matlab源码 636期】 点击上面蓝色字体,直接付费下载,即可。 获取代码方式2: 付费专栏Matlab图像处理(初级版) 备注: 点击上面蓝色字体付费专栏Matlab图像处理(初级版),扫描上面二维码,付费29.9元订阅海神之光博客付费专栏Matlab图
《学一辈子光线追踪》 六 正交基
蒙特卡洛光线追踪技术系列 见 蒙特卡洛光线追踪技术 在最后一章中,我们开发了生成与日晷相对的随机方向的方法。我们要做的是基于任意曲面的法向量。正交正规基(ONB)是三个相互正交的单位向量的集合。笛卡尔xyz轴就是这样的一个ONB,我有时忘记了它必须坐在某个真实的地方,有真实的方向,才能在真实世界中有意义,而在虚拟世界中有一些虚拟的地方和方向。图片是相机和场景相对位置/方向的结果,只要相机和场景在
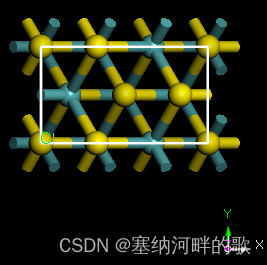
保姆级教程 | Materials Studio中将斜方晶格转换为正交晶格
背景 由于临时的合作安排中有建立MoS2模型的需求,但MS里自带的.msi结构文件是斜方晶系,后续需要正交晶系方便进一步组合模型进行模拟 步骤 1.在MS里导入MoS2的原胞(原始晶胞) 菜单栏中File - Import D:\MaterialsStudio2019\MaterialsStudio2019_36042\1\Materials Studio 19.1\share\St
数据降维 | Matlab实现POD本征正交分解数据降维模型
数据降维 | Matlab实现POD本征正交分解数据降维模型 目录 数据降维 | Matlab实现POD本征正交分解数据降维模型基本介绍模型描述程序设计 基本介绍 1.Matlab实现POD本征正交分解数据降维模型(完整源码和数据); 2.运行环境matlab2023; 3.POD降维,POD分解(Proper Orthogonal Decomposition)(PO
线性代数精华——从正交向量到正交矩阵
本文始发于个人公众号:TechFlow 向量内积 这个基本上是中学当中数学课本上的概念,两个向量的内积非常简单,我们直接看公式回顾一下: X ⋅ Y = ∑ i = 1 n x i ∗ y i X \cdot Y = \sum_{i=1}^n x_i*y_i X⋅Y=i=1∑nxi∗yi 这里X和Y都是n维的向量,两个向量能够计算内积的前提是两个向量的维度一样。从上面公式可
现代通信原理14.1:正交向量空间与正交信号空间
文章目录 1、向量空间1.1 向量空间的概念1.2 向量的内积1.3 向量的范数1.4 标准正交向量组1.5 Gram-Schmidt正交化1.6 向量的正交表示 2、信号空间2.1 信号的能量2.2 信号的内积2.3 信号的范数2.4 信号的相关系数2.5 信号的正交展开2.6 信号的向量表示 1、向量空间 1.1 向量空间的概念 在线性代数中,我们学习了向量与向
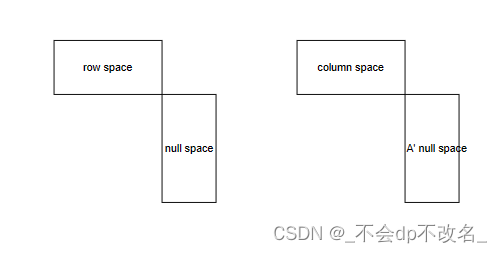
线性代数笔记13--正交向量和正交子空间
0. 四个子空间 1. 正交向量 两向量点乘为0,向量正交。 A ⊤ B = 0 A^{\top}B=0 A⊤B=0 勾股定理 ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y 2 ∣ ∣ = ∣ ∣ x + y ∣ ∣ 2 ||x||^2+||y^2||=||x+y||^2 ∣∣x∣∣2+∣∣y2∣∣=∣∣x+y∣∣2 验证正交条件 ∣ ∣ x ∣ ∣ 2 = x ⊤ x = x x ⊤
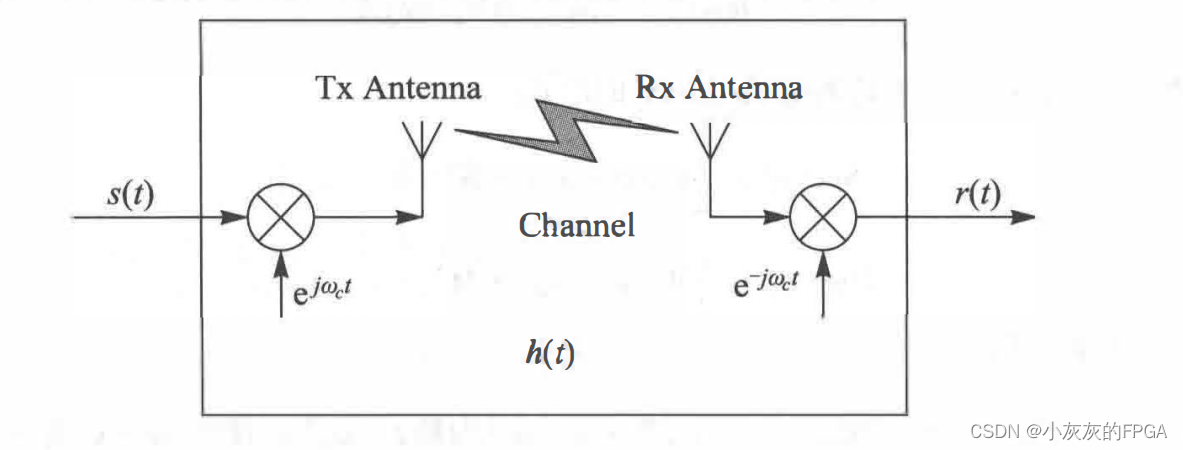
通信入门系列——IQ(同相正交)调制
微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等 本节目录 一、单边带与双边带信号比对二、IQ(同相正交)调制技术三、IQ信号的复数表达式 本节内容 一、单边带与双边带信号比对 如何理解单边带信号只需要一半的频谱资源? 双边带频谱可