本文主要是介绍通信入门系列——IQ(同相正交)调制,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录
一、单边带与双边带信号比对
二、IQ(同相正交)调制技术
三、IQ信号的复数表达式
本节内容
一、单边带与双边带信号比对
如何理解单边带信号只需要一半的频谱资源?
双边带频谱可以表示为s(t)cos(ωct),单边带频谱可以表示为s(t)cos(ωct)-s ~ (t)sin(ωct),其中s ~ (t)表示希尔伯特变换后信号。根据三角函数关系式,单边带信号可以表示为A(t)cos(ωct+φ(t)),其中A(t)是幅度,是s(t)平方与s~(t)平方的和的开方,φ表示的是相位,tanφ(t)=-s ~ (t)/s(t)。
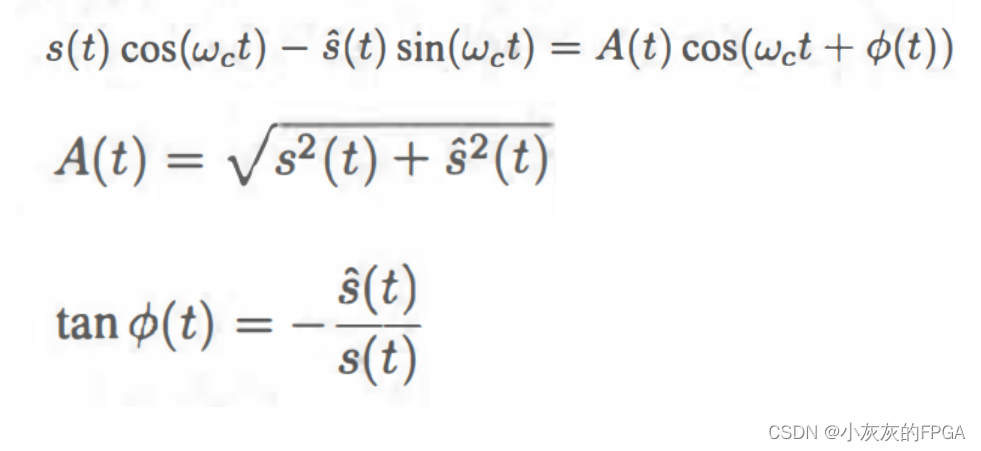
通过比较单边带信号和双边带信号的公式,可以看出单边带信号同时利用了载波的幅度和相位,也就是正弦和余弦两个正交分量都使用了,而双边带信号则值利用了载波的幅度,即余弦分量。由此可以看出单边带多了一倍的信息,但只需要一半的频谱资源。
单边带信号是否只要满足上述关系就能成功节省一半资源?
双边带信号的一个边带消除后就变成单边带信号,但需要对正弦分量通过希尔伯特变换进行约束,保证在接收侧的正弦分量和余弦分量相同。这样才能保证在带宽一致的情况下,单边带信号可以传输同样的信息。
二、IQ(同相正交)调制技术
IQ(同相正交)调制技术,用来替换希尔伯特变换。希尔伯特变换是一个非因果系统,在一时刻的输出,不仅与之前输入信号有关,还与之后的输入信号有关,也就是在时域上实现h(t)=1/(πt)的滤波器很困难。还有一种就是通过频域相移π/2,不同频率成分做不同的延时,就比较麻烦。因此引入了IQ(In-phase Quadrature)调制技术。
两路正交信号,I路信号为x(t),Q路信号为y(t),分别进行调制乘以cos(ωct)和sin(ωct)后,获得发射信号为x(t)cos(ωct)-y(t)sin(ωct)。在接收端两路通道分别进行cos(ωct)调制和-sin(ωct)调制,然后通过低频滤波器滤除倍频成分,获得x(t)和y(t)。
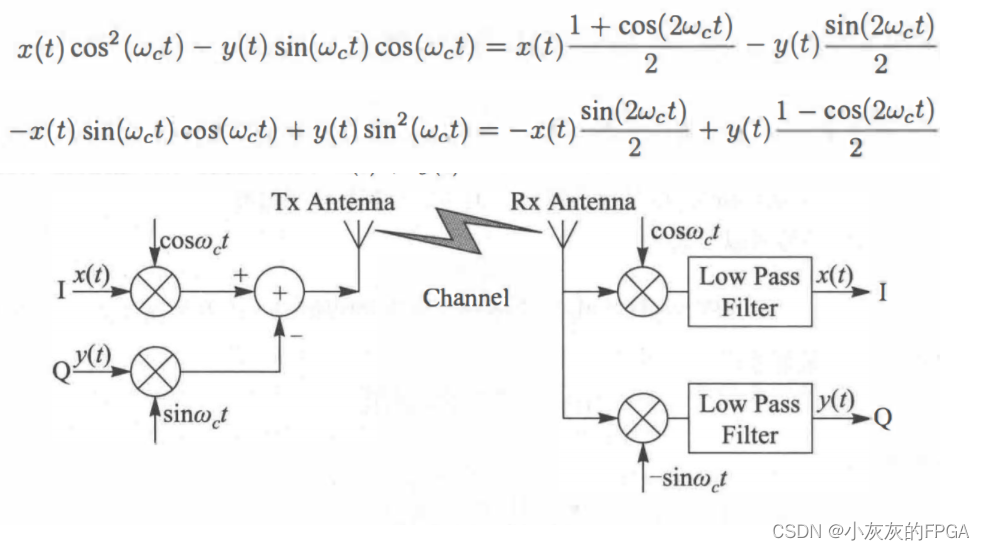
三、IQ信号的复数表达式
IQ调制的复数表达,本质上,在发射端,复基带信号x(t)+jy(t)被负载波信号e(jωct)调制。而在接收端,用e(-jωct)进行解调从而获得复基带信号。
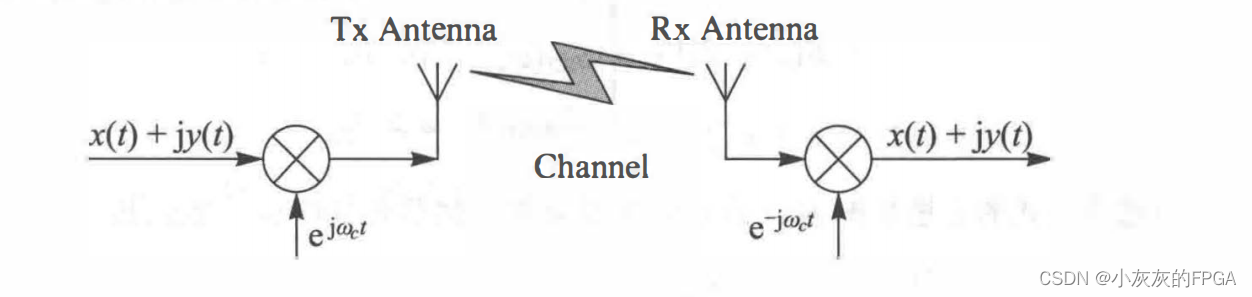
接收机的复基带信号是发射机复基带信号经过一个复数信道的响应。IQ调制的信号是一个实数信号,用复数信号s(t)e^(jωct)来表达,其中s(t)为复基带信号。接收信号以及信道的冲激响应都是实数信号,均可以用复数来表示,复基带信号之间满足卷积:r(t)=s(t)*h(t)。
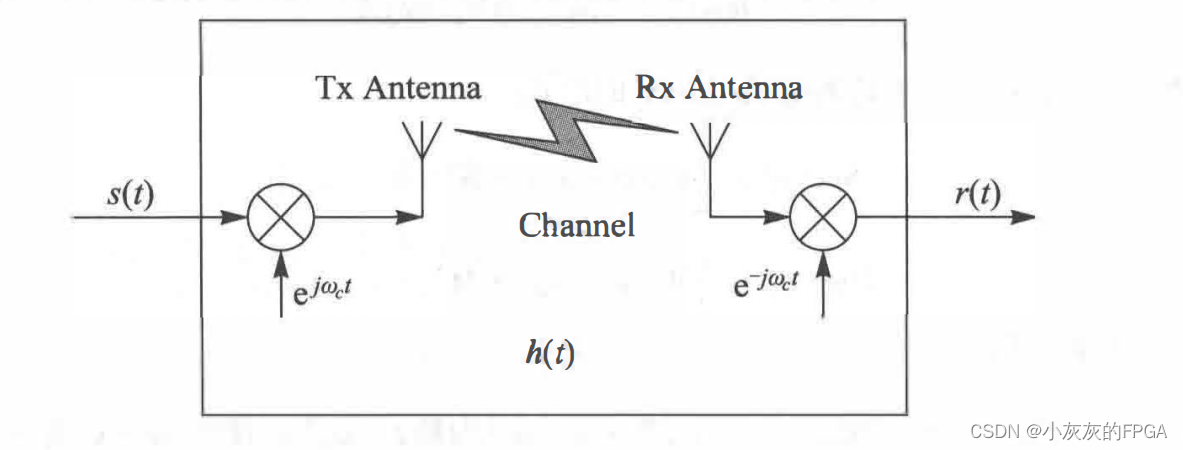
这篇关于通信入门系列——IQ(同相正交)调制的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






