欧式专题

Matlab）实现HSV非等间隔量化--相似判断：欧式距离--输出图片-

%************************************************************************** % 图像检索——提取颜色特征 %HSV空间颜色直方图(将RGB空间转化为HS

常用的相似度计算方法----欧式距离、曼哈顿距离、马氏距离、余弦、汉明距离、切比雪夫距离、闵可夫斯基距离、马氏距离

在深度学习以及图像搜索中，经常要对特征值进行比对，得到特征的相似度，常见的特征值比对方法有汉明距离、余弦距离、欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离等，下面对各种比对方法分别进行介绍。目录 1汉明距离 2余弦相似度 3欧式距离 4曼哈顿距离 5切比雪夫距离 6闵可夫斯基距离 7马氏距离 1汉明距离汉明距离/Hamming Distance也能用来计算两

数学基础之曼哈顿距离，欧式距离，余弦距离

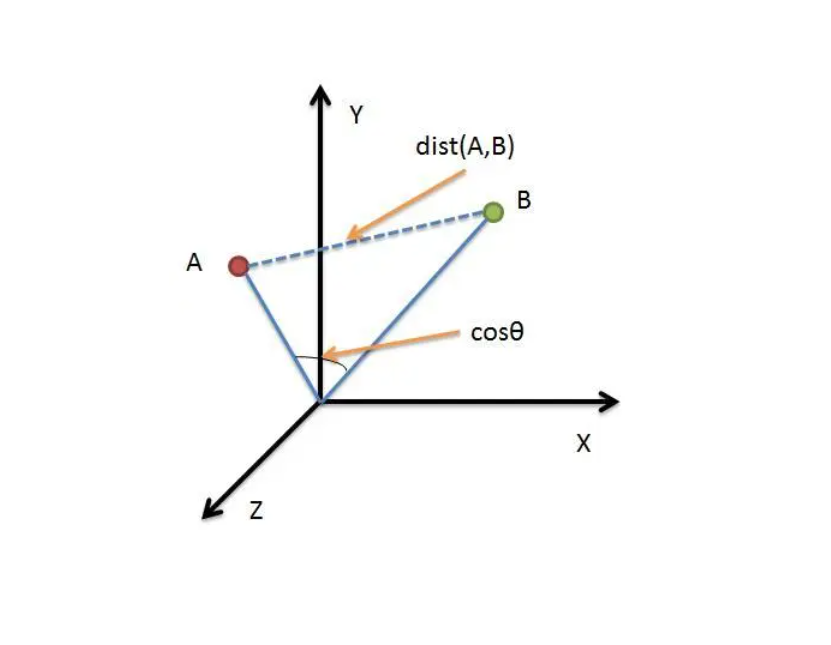
曼哈顿距离，欧式距离，余弦距离 1.曼哈顿距离曼哈顿距离又称马氏距离（Manhattan distance），还见到过更加形象的，叫出租车距离的。具见上图黄线，应该就能明白。计算距离最简单的方法是曼哈顿距离。假设，先考虑二维情况，只有两个乐队 x 和 y，用户A的评价为(x1,y1)，用户B的评价为(x2,y2)，那么，它们之间的曼哈顿距离为 2.欧式距离欧式距离

欧式距离分析情感值

测试和训练文本：文本编号词列表（以空格分隔）公众"感动"的概率训练文本1 消防员冲进火场救出男童 1 训练文本2 公务员患癌症保持在岗 0.9 训练文本3 消防员多次冲进火场救人不幸身亡 0.5 训练文本4 老人成功进行免费白内障手术 0.5 训练文本5 海豚误吞排球后手术成功取出 0.4 训练文本6 6旬老人跳楼自杀身亡 0.

【数据挖掘】机器学习中相似性度量方法-欧式距离

写在前面：首先感谢兄弟们的订阅，让我有创作的动力，在创作过程我会尽最大能力，保证作品的质量，如果有问题，可以私信我，让我们携手共进，共创辉煌。路虽远，行则将至；事虽难，做则必成。只要有愚公移山的志气、滴水穿石的毅力，脚踏实地，埋头苦干，积跬步以至千里，就一定能够把宏伟目标变为美好现实。最近在做实际项目时，遇到需要计算两个向量的相似性，即需要计算不同数据样本之间的相似度。计算样本之间

欧式聚类提取-------PCL

欧式聚类 std::vector<pcl::PointCloud<pcl::PointXYZ>::Ptr> PclTool::euclideanClustering(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud){std::vector<pcl::PointCloud<pcl::PointXYZ>::Ptr> clustered_clouds

$Python-Numpy-计算向量间的欧式距离$

Python-Numpy-计算向量间的欧式距离

两个向量间的欧式距离公式： a = np.array([[2, 2], [4, 5], [6, 7]])b = np.array([[1, 1]])# 使用L2范数计算dev1 = np.linalg.norm(a - b, ord=2, axis=1)# 使用公式计算dev2 = np.sqrt(np.sum((a - b) ** 2, axis=1))print(dev1.r

图像变换：刚性变换(等距变换、欧式变换)、相似变换、仿射变换、射影变换(透视变换、投影变换)

刚性变换(等距变换、欧式变换)、相似变换、仿射变换、射影变换(透视变换、投影变换) 1.刚性变换：只对物体进行平移和旋转，而形状不变 2.相似变换：等距变换 + 均匀缩放，类似相似三角形，比例不变 3.仿射变换：旋转+平移+缩放+切变shear，保持平行性 4.透视变换：旋转+平移+缩放+切变+射影在三维空间上进行变换：不保留平行性射影变换的不变量是:

欧式风格色调高雅新古典风格设计

高雅而和谐是新古典风格的代名词。白色、金色、黄色、暗红是欧式风格中常见的主色调，少量白色糅合，使色彩看起来明亮、大方，使整个空间给人以开放、宽容的非凡气度，让人丝毫不显局促。(幸福空间供稿) 　　案例一：185平奢华风格大户型　　主要建材：皮革、茶镜、烟波山水大理石、玉晶石、白金琉璃石材、金箔　　风格定调在低调奢华，又兼具现代时尚的氛围，暖色基础加以垂直、水平线的变化，其中还利用少见

欧式空间和非欧空间

转载自：微信公众号：算法与数学之美欧几里得的世界一条直线L和不在L上的点P，经过P点平行于L的线有几条？在欧式空间中，这个问题显然是“只有一条”，然而在非欧空间中，这个问题就不一定了。马鞍形的双曲抛物面，就是一个非欧空间的例子。现实中，非欧空间的例子还很多。下图中，粉色和黄色线都平行于蓝线，且都经过同一点。更重要的是，蓝色和黄色的平行线并非与欧式空间中的平行线一样处处

[点云分割] 欧式距离分割

效果：代码： #include <iostream>#include <chrono>#include <pcl/ModelCoefficients.h> // 模型系数的定义#include <pcl/io/pcd_io.h>#include <pcl/point_types.h> // 各种点云数据类型#include <pcl/sample_consensus/met

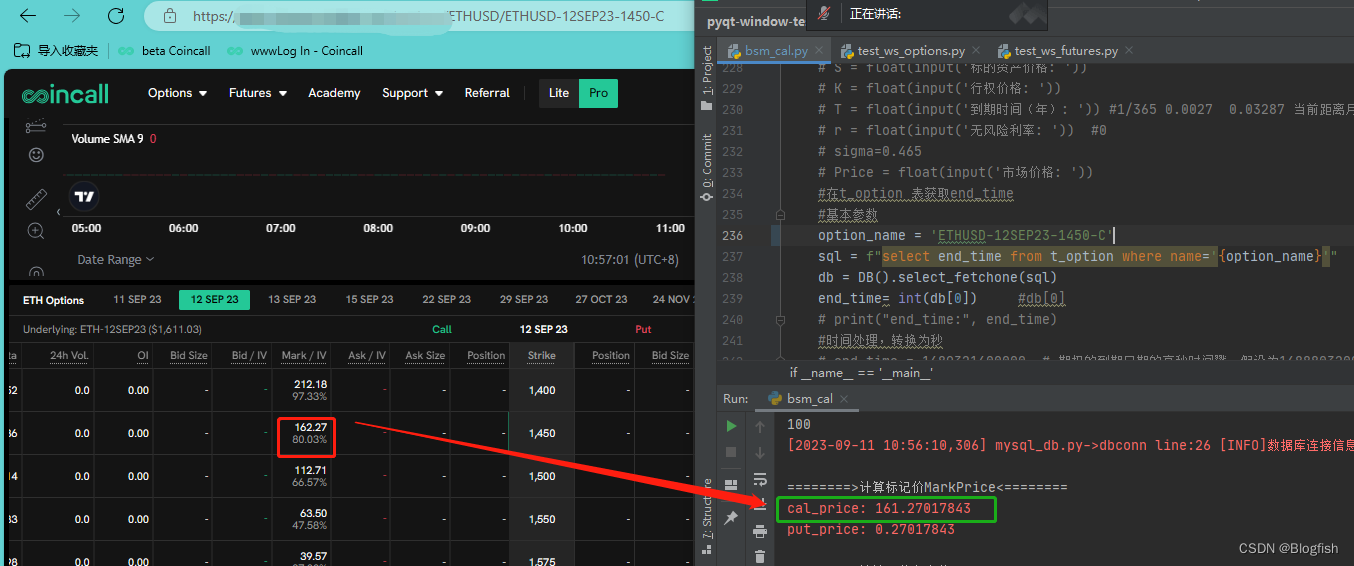
Python使用BS定价公式计算欧式期权标记价(MarkPrice)

影响标记价格的几个要素是标的资产价格（即标的价格）、行权价、到期日(可以是天或秒，使用秒计算更精确)、无风险利率、隐含波动率。若要计算看涨(即Call)和看跌(Put)的标记价，还需要计算两个中间参数。一个参数用于计算认购(即看涨Call)期权的价格，一个参数用于计算认购或认沽(即看跌Put)价格。用到知识点是正太分布累计概率和正太分布概率密度函数，需要引入的库

付费系列 7 - 双资产欧式期权 2D PDE 有限差分

本帖开始双资产（标的）欧式期权的二维 PDE 有限差分定价。产品包括互换期权、绩优期权、较佳/较差期权、最大看涨/看跌期权、最小看涨/看跌期权、基差期权、算术/几何篮子期权。本帖目录如下：各种产品的支付函数如下：用偏微分方程有限差分对期权定价分五步：方程解域 (solution domain)网格打点 (grid construction)终边条件 (terminal and bo

QuantLib 金融计算——案例之普通欧式期权分析

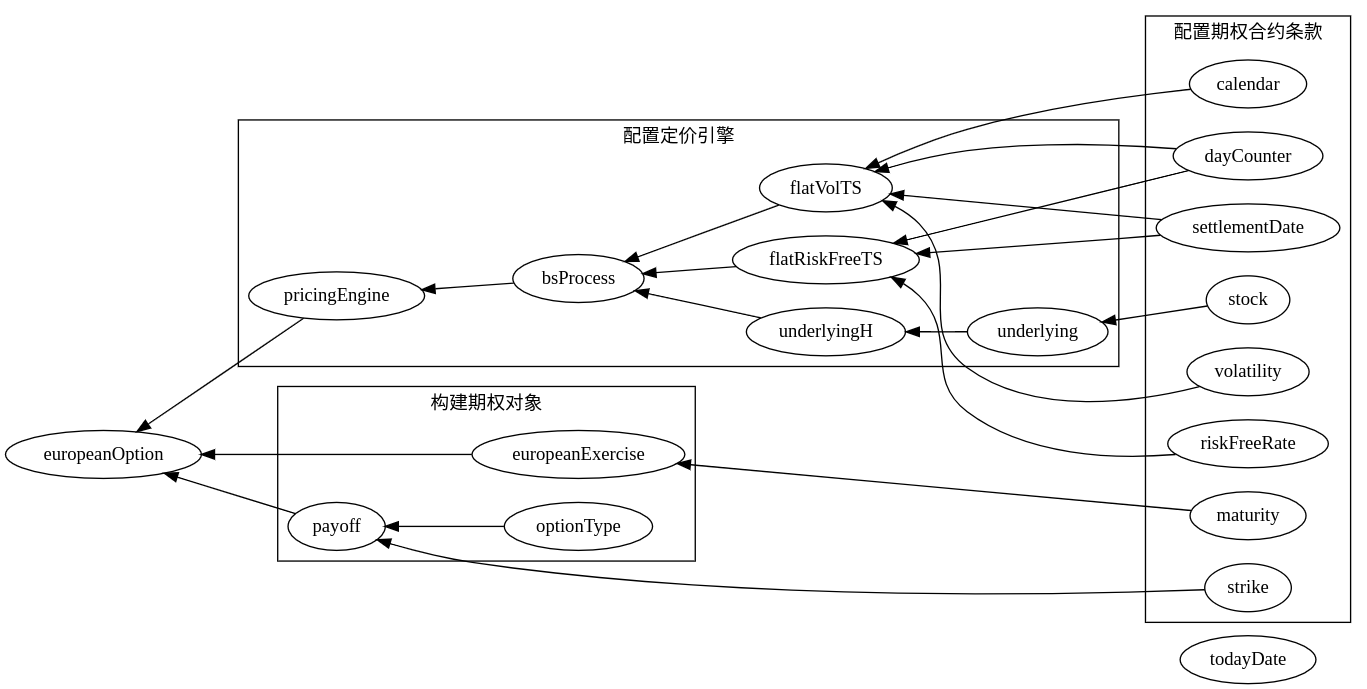
目录 QuantLib 金融计算——案例之普通欧式期权分析概述普通欧式期权公式法定价 1. 配置期权合约条款2. 构建期权对象3. 配置定价引擎4. 计算题外话：天数计算规则Quote 带来的便利总结如果未做特别说明，文中的程序都是 python3 代码。 QuantLib 金融计算——案例之普通欧式期权分析载入 QuantLib 和其他包： import QuantLib a

采用蒙特卡洛模拟方法计算欧式期权的价值--python

信息： 1、股票指数化水平：s0=100 2、欧式看涨期权行权价格：K=105； 3、到期时间：T=1； 4、固定无风险利率：r=5%; 5、固定波动率：&=20%；代码： so=100 K=105 T=1 r=0.05 sigma=0.2 from numpy import* I=100000 z=random.standard_normal(I) st=so*exp((r

[欧式几何]与[非欧几何]の圆的面积（洛谷P4326题题解，Java语言描述）

题目要求 P4326题目链接分析欧式几何下圆的面积： S = πr2 闵可夫斯基几何下圆的形状换成我们习惯的平面直角坐标系是：没错，是个正方形！！！ S = √2 r × √2 r = 2r2 所以本题易解，借助一下Math.PI就好啦…… 保留一下小数后六位即可，System.out.printf()…… AC代码（Java语言描述） import java.uti

学习用3DSMAX制作漂亮的欧式古典客…

学习用3DSMAX制作漂亮的欧式古典客厅效果图，教程中，我主要探讨了制作新古典客厅的渲染和照明调整，在第一个实例中，我激活了Maxwell渲染，将Material Editor中的材质设置为Maxwell材质。图01中的数值表明了场景中照明位置的设置。我想把场景创建出真实效果，因此根据现实生活中光线的角度设置了照明。在这个场景中我选择了把照明资源变成立方体。学习加3Dmax室内

基于matlab点云工具箱对点云进行处理四：对点云进行欧式聚类，并获得包围点云簇的外接凹多边形

基于matlab点云工具箱对点云进行处理四：对点云进行欧式聚类，并获得包围点云簇的外接凹多边形步骤：读取velodyne数据包pcap文件内的点云数据使用pcdownsample函数对点云数据进行体素化采样，减少点云数量使用find函数对点云进行筛选使用pcdnoise去除点云内的噪声使用pcsegdist进行欧式聚类使用boundary获得外包顶点对顶点进行整理，输出相关程序代码点

基于matlab点云工具箱对点云进行处理三：对点云进行欧式聚类，使用三角剖分处理后获取点云簇的外接凸多边形

基于matlab点云工具箱对点云进行处理三：对点云进行欧式聚类，使用三角剖分处理后获取点云簇的外接凸多边形步骤：读取velodyne数据包pcap文件内的点云数据使用pcdownsample函数对点云数据进行体素化采样，减少点云数量使用find函数对点云进行筛选使用pcdnoise去除点云内的噪声使用pcsegdist进行欧式聚类使用delaunayTriangulation进行三角剖分使

基于matlab点云工具箱对点云进行处理二：对点云进行欧式聚类，获得聚类后点云簇的外接矩形

基于matlab点云工具箱对点云进行处理二：对点云进行欧式聚类，获得聚类后点云簇的外接矩形步骤：读取velodyne数据包pcap文件内的点云数据使用pcdownsample函数对点云数据进行体素化采样，减少点云数量使用find函数对点云进行筛选使用pcdnoise去除点云内的噪声使用pcsegdist进行欧式聚类使用自定义函数getBoundary获得外接矩形，函数具体定义见附件相关

史上最简SLAM零基础解读(1) - 旋转平移矩阵→欧式变换推导

本人讲解关于slam一系列文章汇总链接:史上最全slam从零开始有兴趣的朋友可以加微信 17575010159 相互讨论技术 - 文末公众号也可关注一、前言(线性变换) 该篇博客主要讲解一个 slam 中最基础的几个东西，那就是旋转矩阵，缩放矩阵以及偏移矩阵。本人会做一个比较细致的讲解。首先从二维平面开始引入，等大家略微了解之后，再扩展到三维。在讲解之前，聊一下其他的东西，那就是