本文主要是介绍Python使用BS定价公式计算欧式期权标记价(MarkPrice),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
影响标记价格的几个要素是标的资产价格(即标的价格)、行权价、到期日(可以是天或秒,使用秒计算更精确)、无风险利率、隐含波动率。
若要计算看涨(即Call)和看跌(Put)的标记价,还需要计算两个中间参数。一个参数用于计算认购(即看涨Call)期权的价格,一个参数用于计算认购或认沽(即看跌Put)价格。
用到知识点是正太分布累计概率和正太分布概率密度函数,需要引入的库是nump、scipy、norm、math,详细见实现过程。
1、导入必备的库
from math import log, sqrt, exp from scipy.stats import norm import numpy as np from scipy import optimize
''' # S 底层资产价格,即标的价格(官方为标的资产价格) # K 期权执行价格,strike price 行权价 # T 期权的剩余期限,单位:年 合约到期时间,如果到期日不足一天需要换算成天,然后除以365(总小时/24) # r 无风险收益率,数字货币市场一般为0, 0即可 # sigma 底层资产价格年化波动率,标记价的隐含波动率,去redis查 d1()、 d2() 说明: 这两个参数在期权定价模型中起到关键的作用,尤其在使用 Black-Scholes 期权定价模型时。 这个模型是一种用来估计欧式期权价格的数学公式。它假设市场是有效的,并且标的资产价格的变动服从几何布朗运动。 根据这个模型,可以使用 d1 和 d2 来计算认购期权和认沽期权的价格。 '''def d1(S, K, T, r, sigma):'''d1 是一个中间参数,用于计算认购期权的价格'''return (log(S / K) + (r + sigma ** 2 / 2.) * T) / (sigma * sqrt(T))def d2(S, K, T, r, sigma):'''d2 是另一个中间参数,用于计算认购期权和认沽期权的价格之间的关系'''return d1(S, K, T, r, sigma) - sigma * sqrt(T)def call_price(S, K, T, r, sigma):'''标记价计算Call'''return S * norm.cdf(d1(S, K, T, r, sigma)) - K * exp(-r * T) * norm.cdf(d2(S, K, T, r, sigma))def put_price(S, K, T, r, sigma):'''标记价计算Put'''return K * exp(-r * T) * norm.cdf(-d2(S, K, T, r, sigma)) - S * norm.cdf(-d1(S, K, T, r, sigma))
2、调用
if __name__ == '__main__':#基本参数option_name = 'BTCUSD-25AUG23-14000-C'sql = f"select end_time from t_option where name='{option_name}'"db = DB().select_fetchone(sql)end_time= int(db[0]) #db[0]#时间处理,转换为秒expiry_date = datetime.fromtimestamp(end_time / 1000) # 将毫秒时间戳转换为datetime对象current_date = datetime.now() # 当前日期和时间time_to_expiry = expiry_date - current_date # 计算到期日与当前日期的时间差time_in_milliseconds = int(time_to_expiry.total_seconds() * 1000) # 将时间差转换为毫秒buy_price = 12486.1 #买一价和卖一价sell_price = 12500 #买一价和卖一价S = 26472.1 # float(input('标的资产价格: '))K = int(option_name.split('-')[-2])T = int(time_in_milliseconds)/1000 # 一天后改为秒sigma = 1.5953 # float(input('隐含波动率: '))r = 0 # 无风险利率# S, K, T, r, sigmaprint("\n========>计算标记价MarkPrice<========")print_color('cal_price: %.8f' % call_price(S, K, T/year_second , r, sigma), fg=Color.RED.value)print_color('put_price: %.8f' % put_price(S, K, T /year_second, r, sigma), fg=Color.RED.value)
代码中在数据库中先获取改期权的到期日,然后换算成秒;输出时加了带颜色的输出。
因受隐含波动率和标的价格影响,小数点后的数值会有偏差。计算结果:
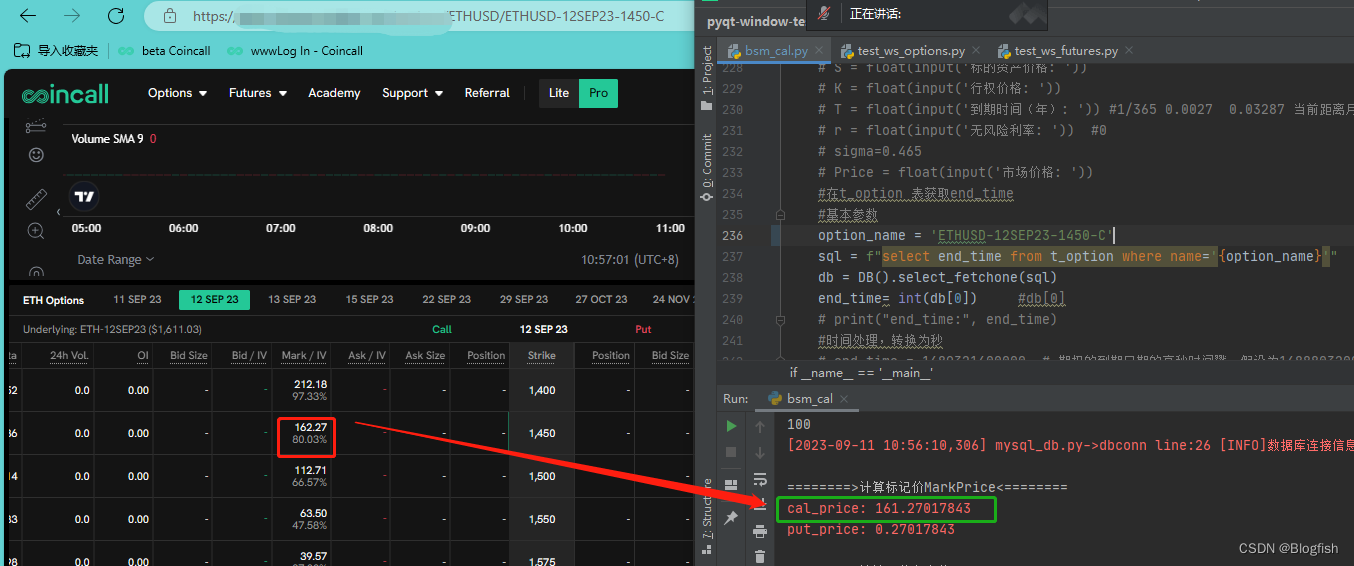
这篇关于Python使用BS定价公式计算欧式期权标记价(MarkPrice)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






