付费系列 7 - 双资产欧式期权 2D PDE 有限差分

本帖开始双资产（标的）欧式期权的二维 PDE 有限差分定价。产品包括互换期权、绩优期权、较佳/较差期权、最大看涨/看跌期权、最小看涨/看跌期权、基差期权、算术/几何篮子期权。

本帖目录如下：

各种产品的支付函数如下：

用偏微分方程有限差分对期权定价分五步：

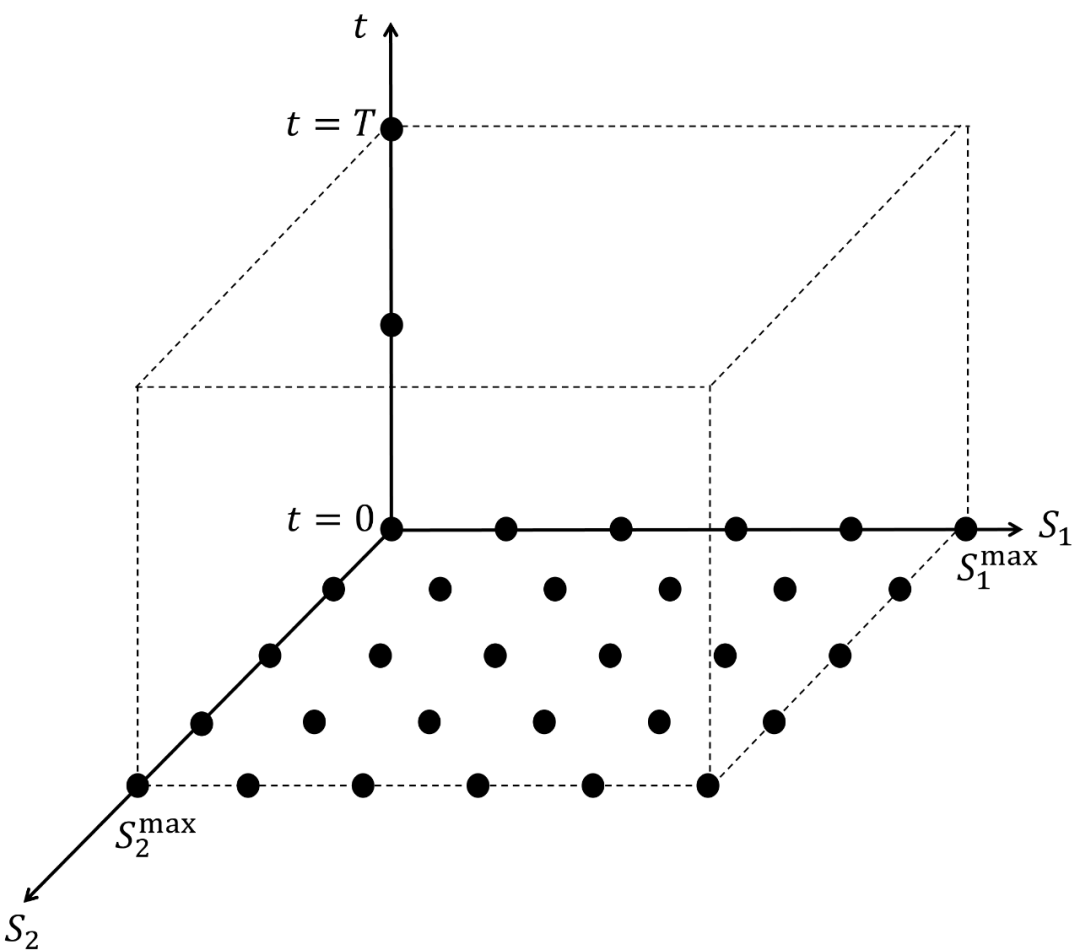
• 方程解域 (solution domain)

• 网格打点 (grid construction)

• 终边条件 (terminal and boundary condition)

• 时空离散 (spatial and time discretization)

• 差分格式 (finite difference scheme)

方程解域和网格打点 

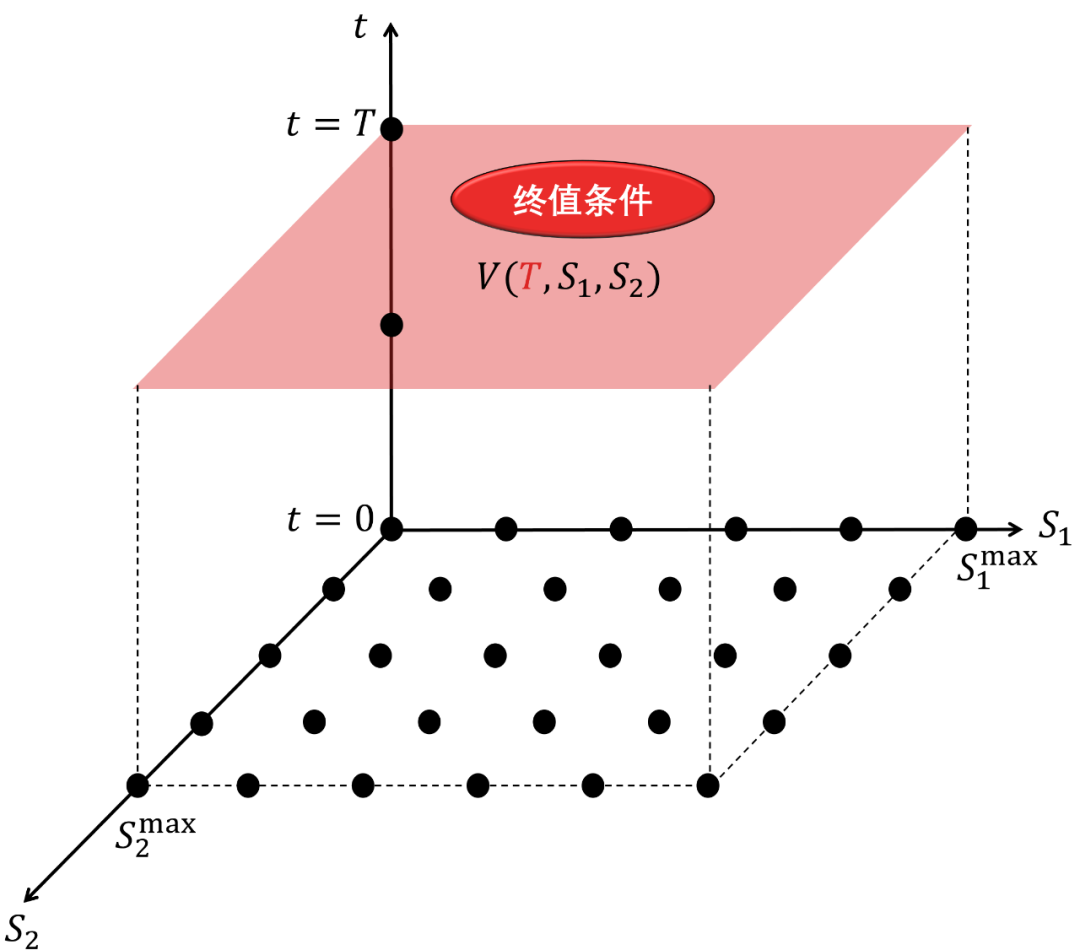
终边条件

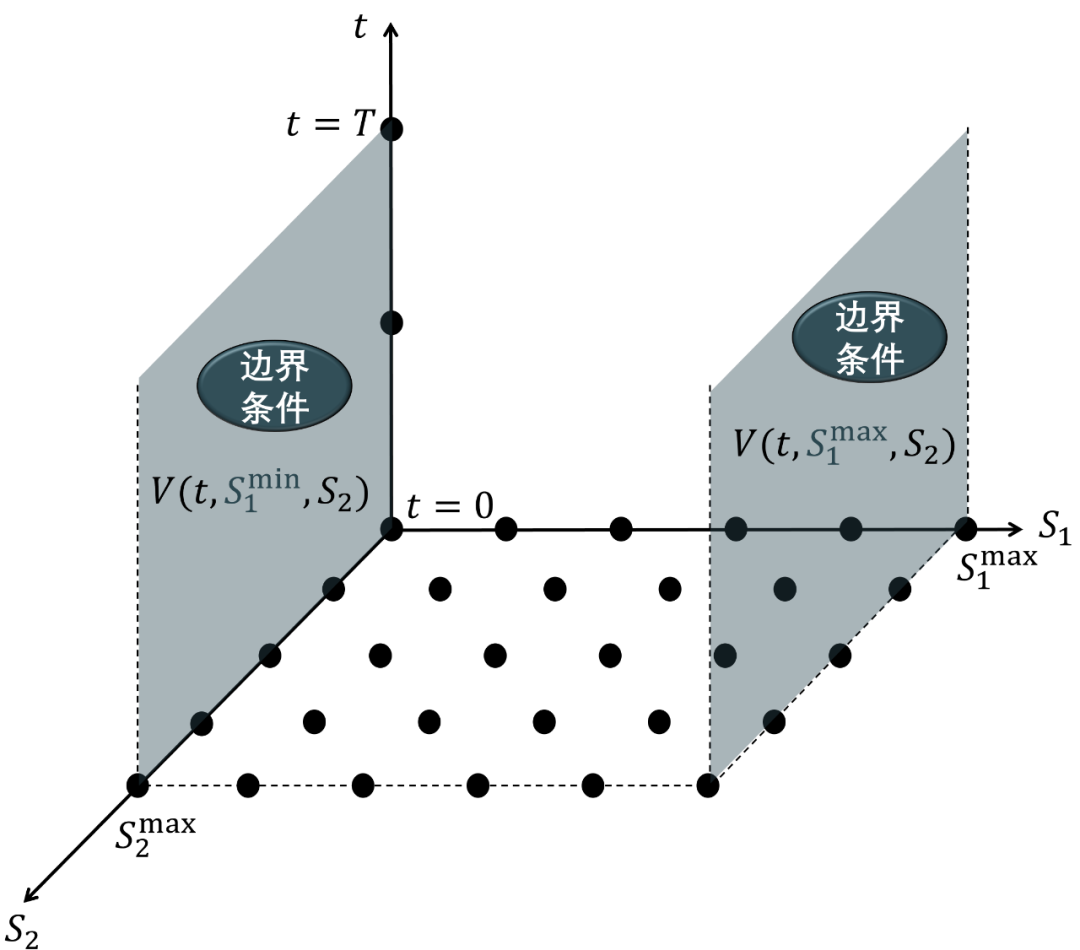
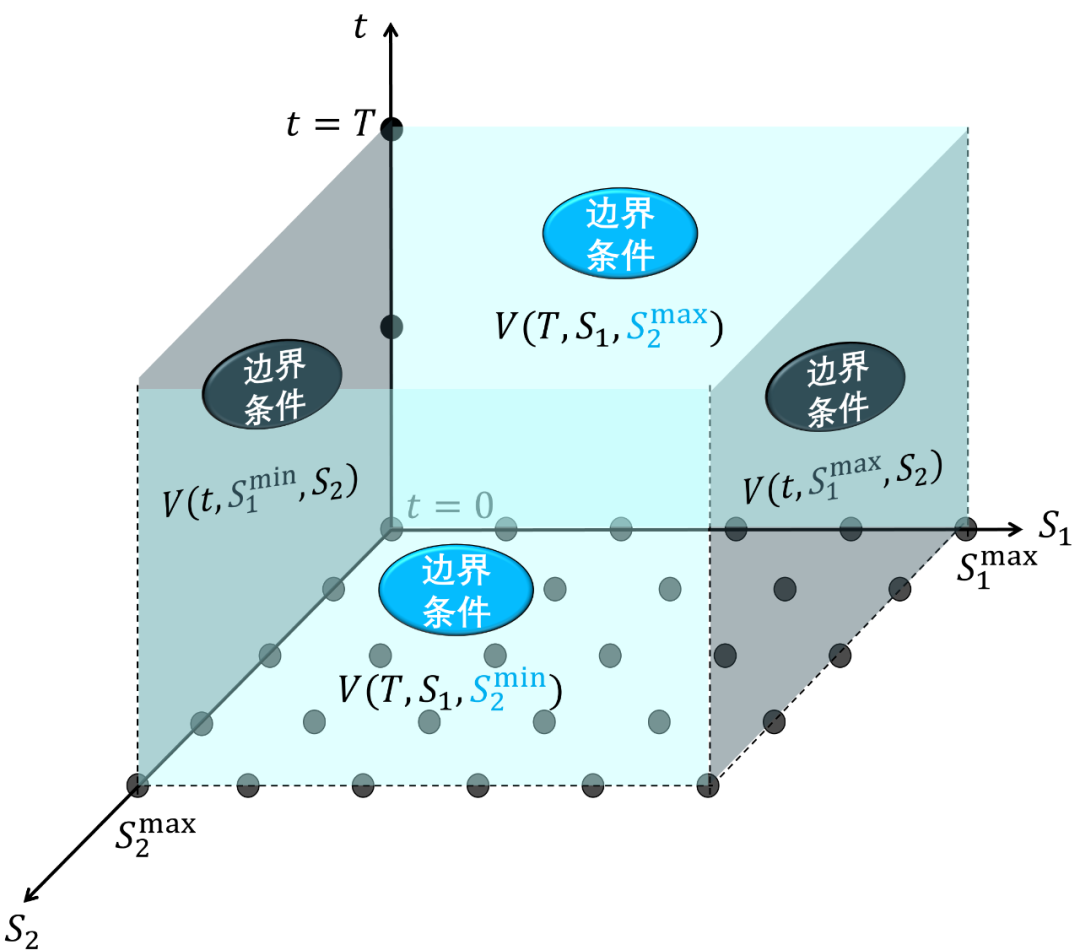
时空离散

在时间 (t) 和空间 (S1, S2) 做完离散后，可以得到如下的 9 对角线稀疏矩阵 (sparse matrix)。

差分格式

需要求解的差分方程如下：

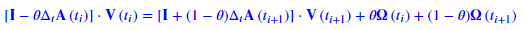
一开始已知终值条件 (红色平面) 和边界条件 (两个蓝色和两个绿色平面)，从 t=T 开始。

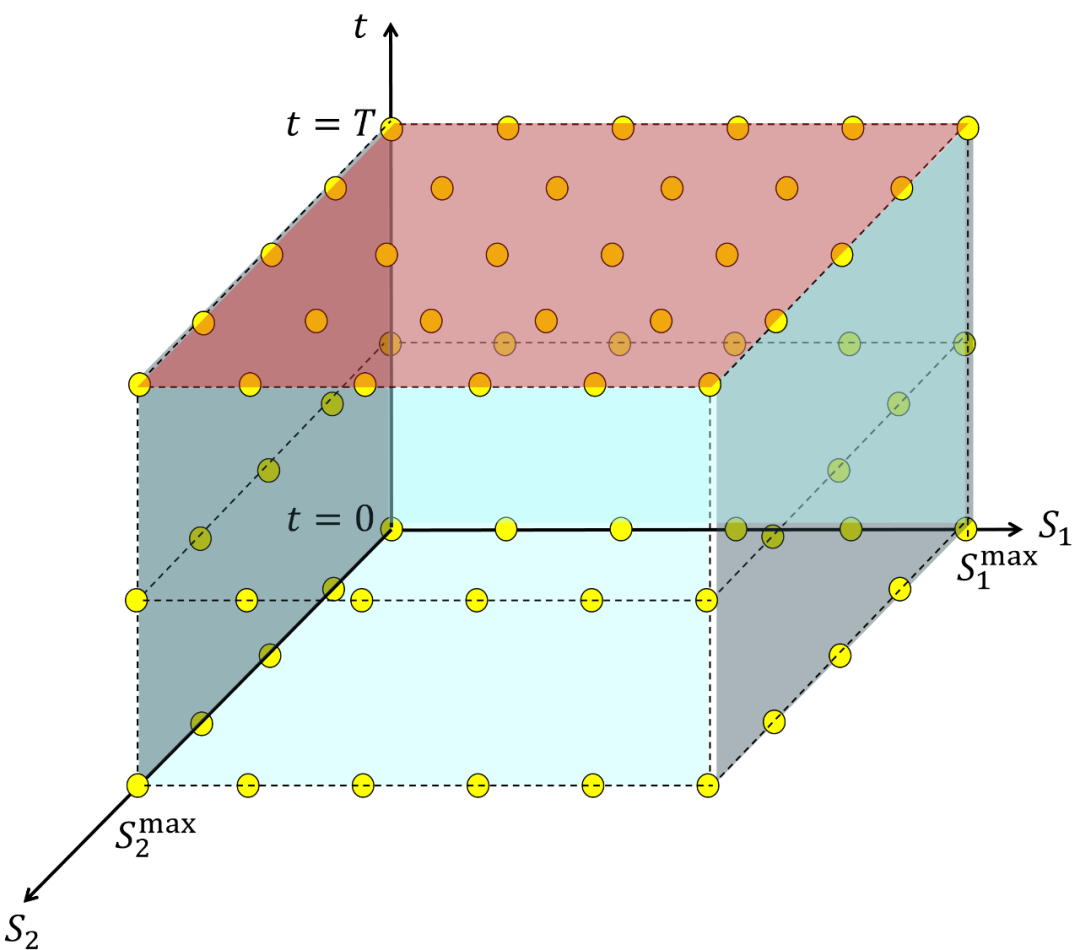
当  ????=????−Δ????  时，求解出黑色平面中的内部点 (interior point)，如下图所示：

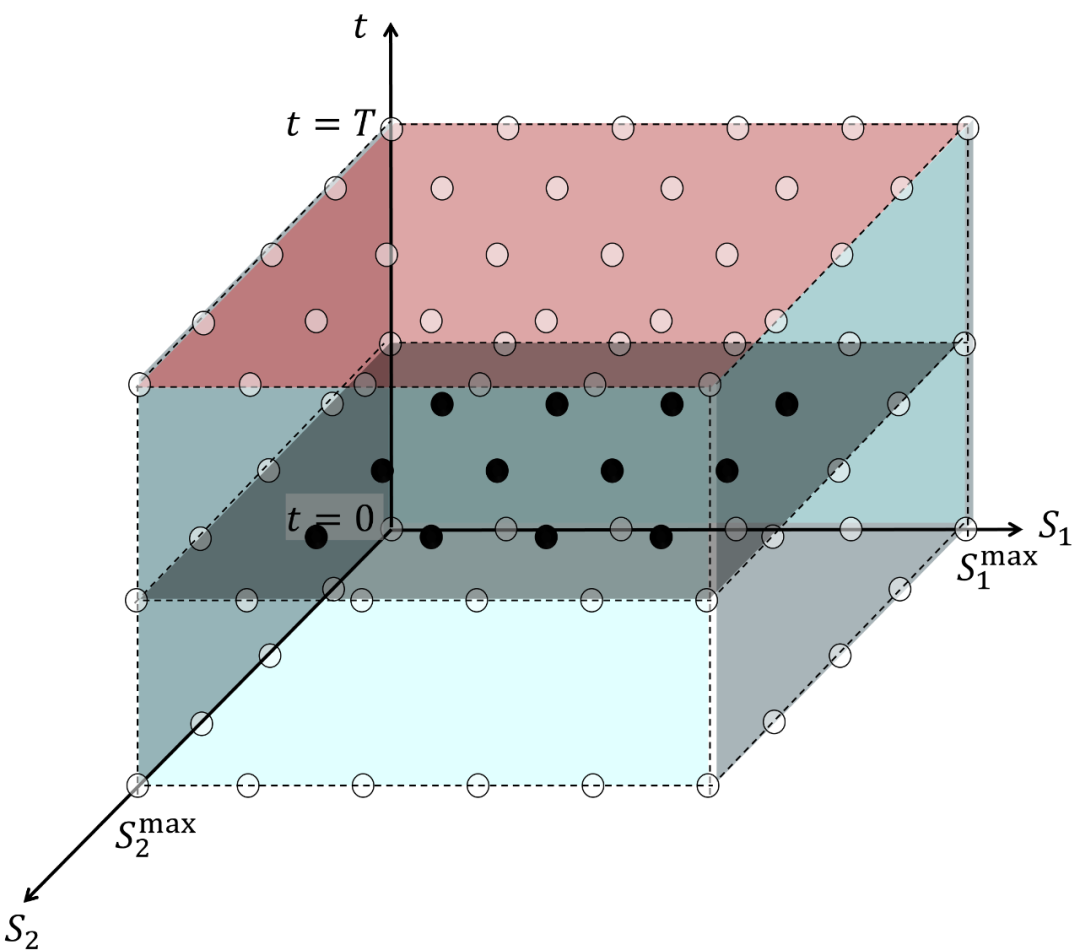
重复上面过程，直到解出 ????=0 时的黑色平面中的内部点，最后根据 ????1(0) 和 ????2(0) 的值，在此平面上二维查出对应的期权值 ????(????1(0),????2(0)) 。

部分代码和结果展示

付费用户（付 1 赠 1）可以获得：

• Python 代码 (Jupyter Notebook)

Jupyter Notebook