pde专题

隐式差分+追赶法求解PDE

前言偏微分方程的求解一般分为两步：（1）利用有限差分构造出三对角矩阵，而有限差分又分为三种：显式差分、隐式差分、C-N差分（即六点差分）有限差分学习笔记-CSDN博客（2）追赶法求解三对角矩阵：三对角矩阵算法（英语：tridiagonal matrix algorithm），又称为托马斯算法（Thomas algorithm，名称源于英国数学家卢埃林·托马斯）是数

PDE_DATA 的定义

PDE_DATA 的定义 Location: /fs/proc/internal.h static inline struct proc_dir_entry *PDE(const struct inode *inode){return PROC_I(inode)->pde;}static inline void *__PDE_DATA(const struct inode

PDE求格林函数

求Green函数通俗地解释拉普拉斯方程的基本解的意义拉普拉斯方程的基本解是一个非常有用的数学概念，它帮助我们理解在某一个点施加一个非常小的影响（比如一个微小的推动、热源或电荷）时，这种影响是如何在整个空间中扩散和影响其他区域的。为了通俗地解释这个概念，我们可以考虑以下几个比喻： 1. 扔石头到静止的水面想象你在一个静止的水塘里扔了一块石头。石头接触水面的那一点，就像是拉普拉斯方程中的

PDE小题

给出二阶偏微分方程 u t t − u x x − u x y = x 2 t u_{tt}-u_{xx}-u_{xy}=x^2t utt−uxx−uxy=x2t 的三维系数矩阵对于二阶偏微分方程 u t t − u x x − u x y = x 2 t u_{tt} - u_{xx} - u_{xy} = x^2t utt−uxx−uxy=x2t，我们可以通过分析每个项的系

保护模式 x86 PDE-PTE中的PWT_PCD位

PDE-PTE中的PWT_PCD位目录文章目录目录先了解CPU缓存PWT 位 [3]PCD 位 [4] 先了解CPU缓存 1>CPU缓存是位于CPU与物理内存之间的临时存储器,他的容量比内存小得多,但是交换速度却比内存要快得多. 2>CPU缓存可以做的很大,有几K,几十K,几百K甚至上M的也有. CPU缓存与TLB的区别: TLB : 线性地址<----->物理地

PDE-GCN:偏微分方程下的图卷积神经网络

NeurIPS 2021文献： PDE-GCN: Novel Architectures for Graph Neural Networks Motivated by Partial Differential Equations 图形神经网络正日益成为各种领域的主流方法计算机视觉、计算生物学和化学等领域的数据这些都可以用图表自然地解释。然而，与传统的卷积神经网络不同网络，深图网络不一定比其他网络

AI求解PDE

一、波动方程的PINN解法： Guo Y, Cao X, Liu B, et al. Solving partial differential equations using deep learning and physical constraints[J]. Applied Sciences, 2020, 10(17): 5917. 二、二维的Navier–Stokes方程组的PINN

12.10多种编码方式，编码方案选择策略（递归级联），PDE，RLE代码

作者如何选择和设计编码方案，以实现高效的解压缩和高压缩比？BtrBlocks是否适用于所有类型的数据？选择和设计编码方案：结合多种高效编码方案：BtrBlocks 通过选择一组针对不同数据分布的高效编码方案，实现高压缩比和快速高效的解压缩。基于采样的方案选择：BtrBlocks 对每个编码方案在样本上进行测试，并选择表现最佳的方案。采样算法在保持相邻元组的局部性和准确表示整个数据范围方面取

matlab的PDE工具箱的简单使用

matlab的PDE工具箱的简单使用_LSEC小陆的博客-CSDN博客_matlab pde pdetool工具箱的使用浅析_DavidEnterpriseStar的博客-CSDN博客_pdetool

迁移学习「求解」偏微分方程，条件偏移下PDE的深度迁移算子学习

本文约3200字，建议阅读5分钟迁移学习框架能够快速高效地学习异构任务。传统的机器学习算法旨在孤立地学习，即解决单个任务。在许多实际应用中，收集所需的训练数据和重建模型要么成本高得令人望而却步，要么根本不可能。迁移学习（TL）能够将在学习执行一个任务（源）时获得的知识迁移到一个相关但不同的任务（目标），从而解决数据采集和标记的费用、潜在的计算能力限制和数据集分布不匹配的问题。来自美国布

付费系列 7 - 双资产欧式期权 2D PDE 有限差分

本帖开始双资产（标的）欧式期权的二维 PDE 有限差分定价。产品包括互换期权、绩优期权、较佳/较差期权、最大看涨/看跌期权、最小看涨/看跌期权、基差期权、算术/几何篮子期权。本帖目录如下：各种产品的支付函数如下：用偏微分方程有限差分对期权定价分五步：方程解域 (solution domain)网格打点 (grid construction)终边条件 (terminal and bo

基于Python编写求解抛物型pde方程的经典数值格式模拟

基于Python编写求解抛物型pde方程的经典数值格式模拟前言一：一维热传导方程简介二：差分格式三：代码实现四：数值结果五：总结前言热方程的在很多领域都有所应用，熟知的在金融领域求解期权定价公式之Black-Scholes方程，就可以用数值格式求解此类方程，因为很多复杂的期权定价公式很难有显式解，数值方法在这方面就有很多优越性。本文将基于Python编写常见的三种数值格式

付费系列 8 - 双资产美式期权 2D PDE 有限差分

本文关注点是双标的美式期权的 PDE FD 解法。在此之前我们已经知道了如何用 PDE FD求解单标的欧式和美式期权，以及求解双标的欧式期权，通过以下类比就可以学到如何用PDE FD 求解双标的美式期权。上式左右两边的“减号”抽象指的是用PDE FD求解美式和欧式之间的差异，而“约等号”抽象指的是单标的和双标的之间差异。符号用法不是很严谨，但主要想传达的信息就是，当你提炼出PDE FD单标

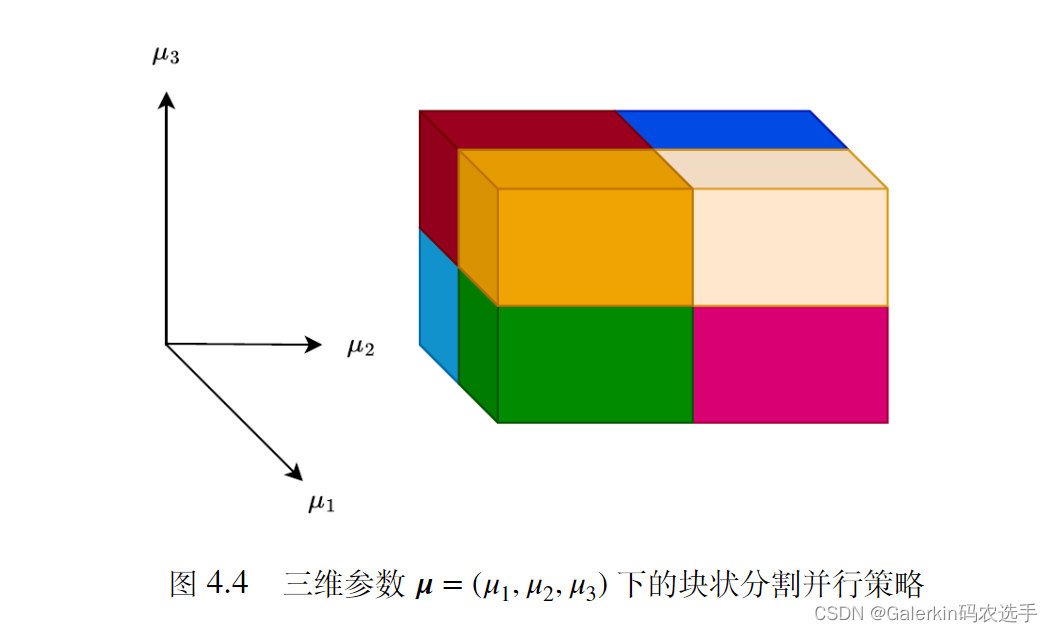
数学系硕士研究生的科研过程——PDE约束下含参优化控制问题的深度学习算法

代码里面的bfgs是我们自己编写的BFGS优化器，可以换成pytorch自带的LBFGS优化器，这里放一下bfgs优化器源代码： bfgs.py # ---------------------------------------------------------------------------------------------------# BFGS Optimizer# The