本文主要是介绍付费系列 8 - 双资产美式期权 2D PDE 有限差分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

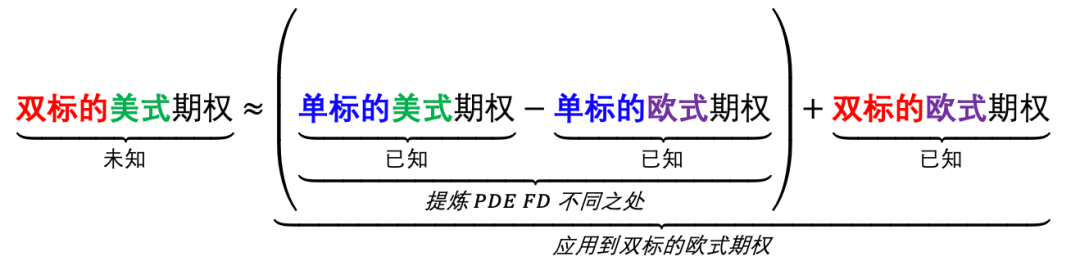
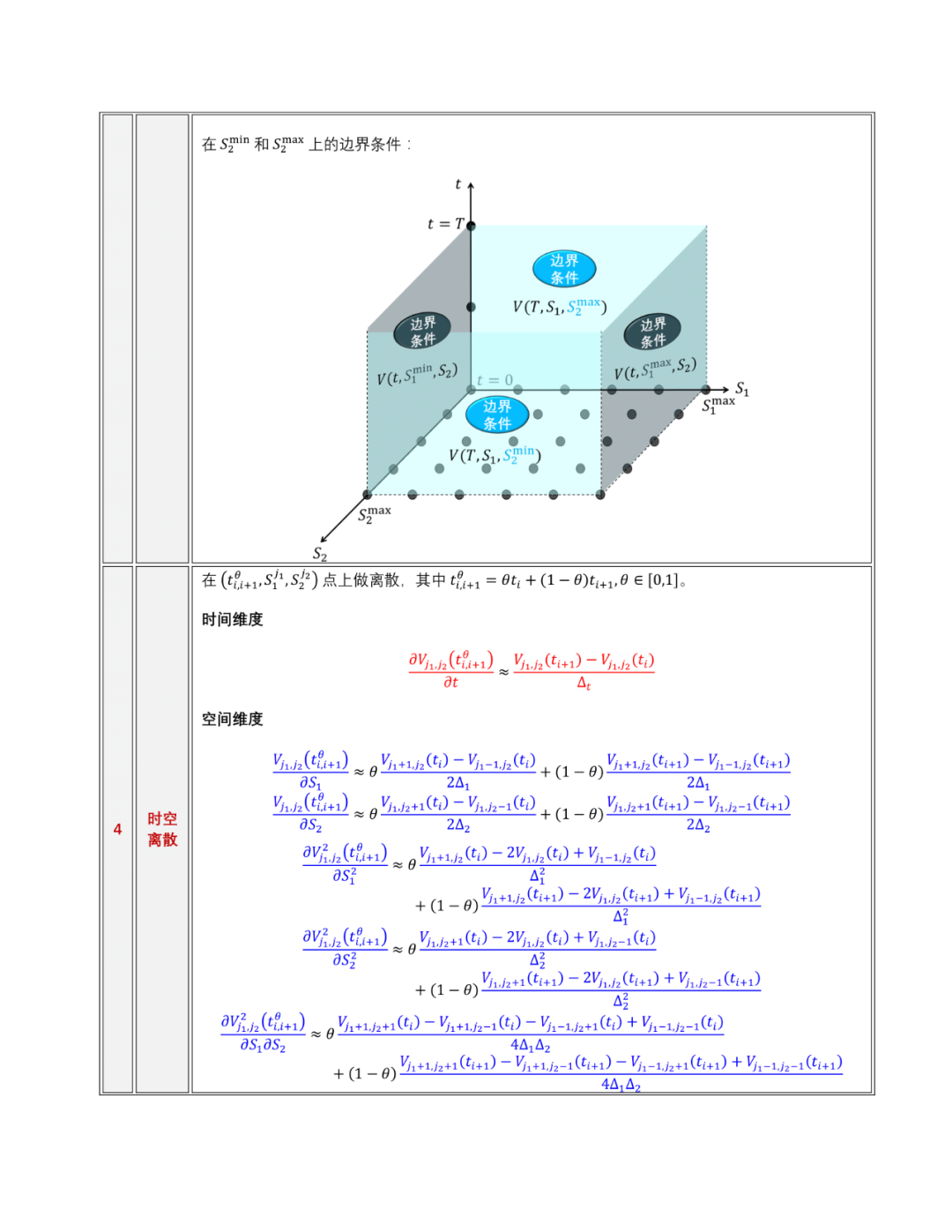
本文关注点是双标的美式期权的 PDE FD 解法。在此之前我们已经知道了如何用 PDE FD求解单标的欧式和美式期权,以及求解双标的欧式期权,通过以下类比就可以学到如何用PDE FD 求解双标的美式期权。

上式左右两边的“减号”抽象指的是用PDE FD求解美式和欧式之间的差异,而“约等号”抽象指的是单标的和双标的之间差异。符号用法不是很严谨,但主要想传达的信息就是,当你提炼出PDE FD单标的欧式和美式期权的不同之处,再把它类比到双标的欧式期权,就能得到双标的美式期权的PDE FD的解法,即







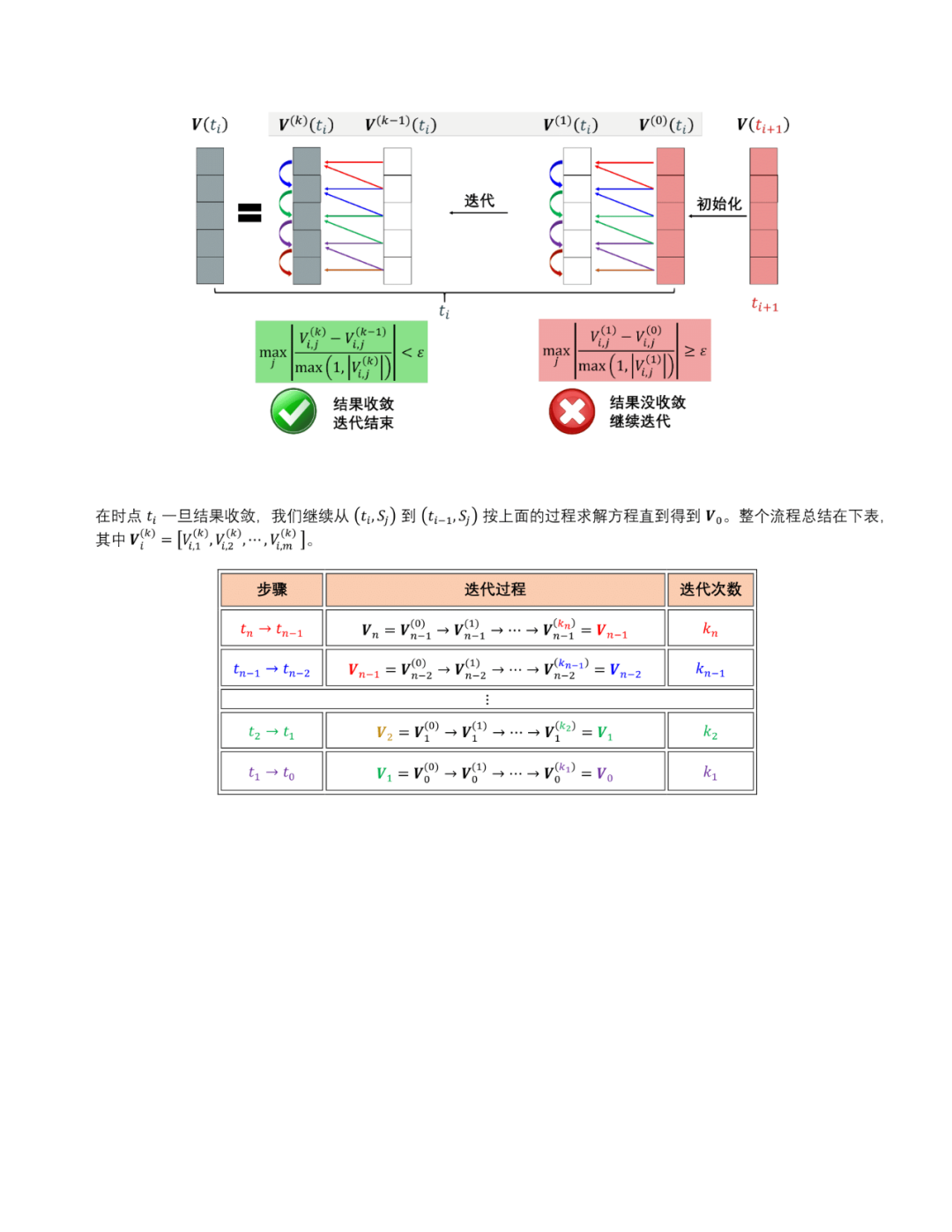

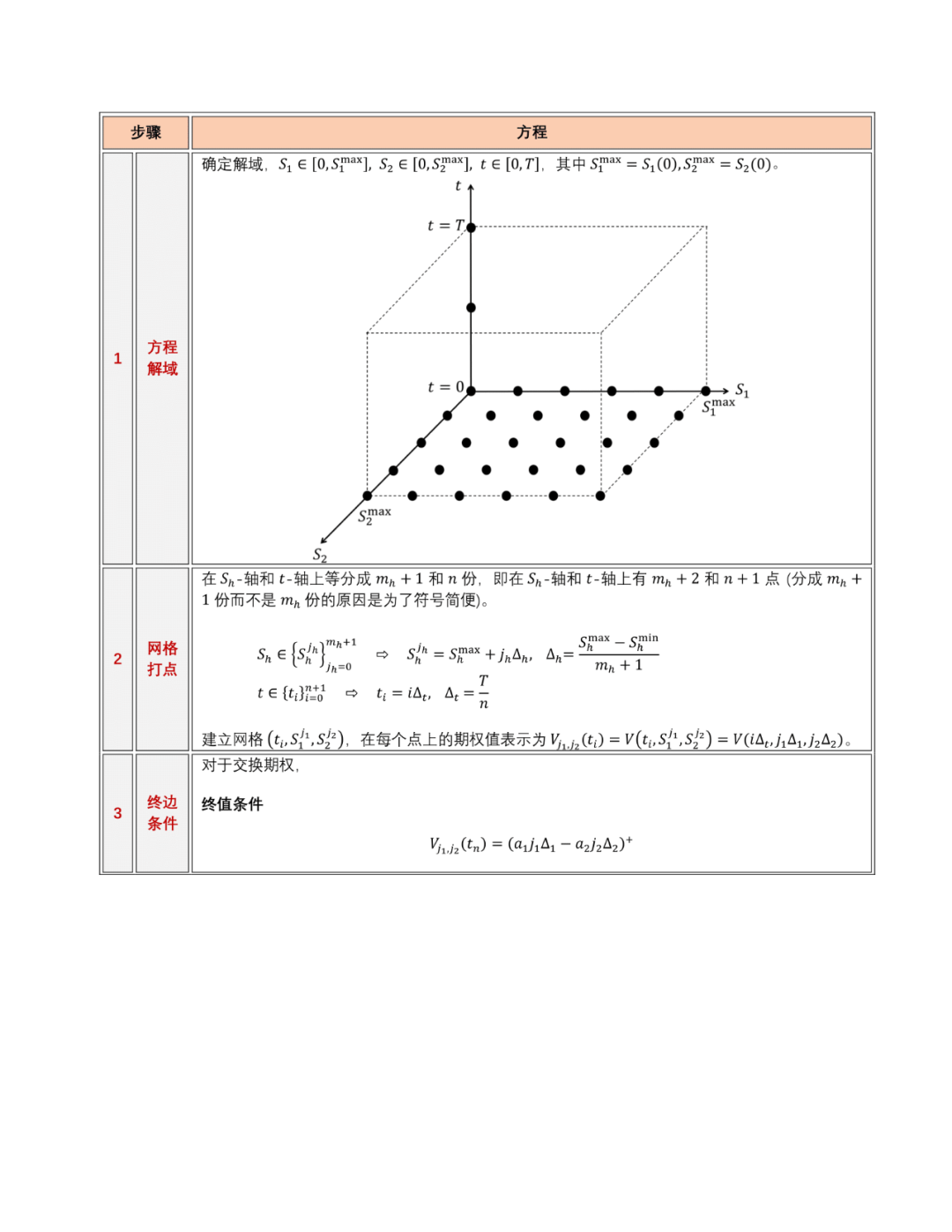
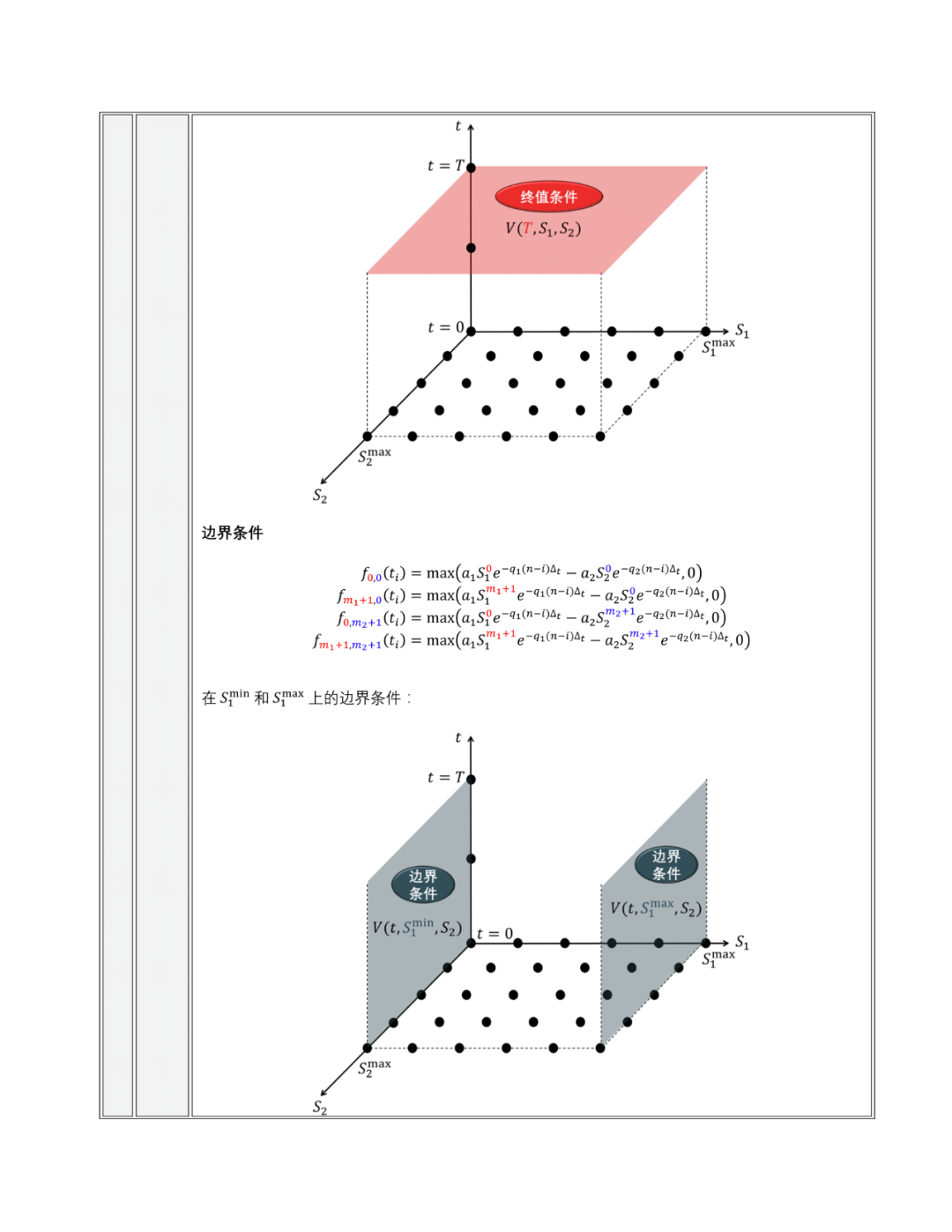






Jupyter Notebook
这篇关于付费系列 8 - 双资产美式期权 2D PDE 有限差分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







