本文主要是介绍PDE求格林函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
求Green函数
通俗地解释拉普拉斯方程的基本解的意义
拉普拉斯方程的基本解是一个非常有用的数学概念，它帮助我们理解在某一个点施加一个非常小的影响（比如一个微小的推动、热源或电荷）时，这种影响是如何在整个空间中扩散和影响其他区域的。为了通俗地解释这个概念，我们可以考虑以下几个比喻：
1. 扔石头到静止的水面
想象你在一个静止的水塘里扔了一块石头。石头接触水面的那一点，就像是拉普拉斯方程中的“点源”。石头落水后，水面上会形成波纹，这些波纹向外扩散，直到消失。拉普拉斯方程的基本解，就类似于描述这种波纹从起始点向外扩散的数学模型。
2. 房间中的烟雾机
如果你在一个封闭的房间里的一个角落放一个烟雾机，烟雾会逐渐填满整个房间。烟雾机的位置就像是拉普拉斯方程的点源，而烟雾的扩散过程就类似于基本解描述的现象——从一个局部点出发，影响逐渐扩展到整个空间。
3. 电灯泡的光
将一个电灯泡放在房间中央，开灯后光线会照亮整个房间。光线从灯泡发出，向四周扩散，照亮每一个角落。在这个例子中，电灯泡是点源，光的扩散就像是拉普拉斯方程的基本解，说明了从一个中心点出发的效果如何逐渐扩展到周围的空间。
结论
在所有这些例子中，拉普拉斯方程的基本解都提供了一个描述点源影响如何随着距离递减的数学表达方式。在物理学中，这种基本解帮助我们计算从点电荷、热源或其他类似“推动”发生的位置，影响是如何传播的。简而言之，拉普拉斯方程的基本解是一种工具，它告诉我们一个小小的局部变化如何影响到整个系统，不论这个系统是水面、空气还是电场。
二维 Laplace 方程基本解的表达式
Γ ( x ; ξ ) \Gamma(\bf{x};\bf{\xi}) Γ(x;ξ) = 1 2 π ln 1 ∣ x − ξ ∣ =\frac{1}{2\pi}\ln\frac{1}{|\bf x-\xi|} =2π1ln∣x−ξ∣1，其中 x , ξ \mathbf{x}, \mathbf{\xi} x,ξ 是 n n n 维向量，当 n = 2 n=2 n=2 时，在二维空间，
∣ x − ξ ∣ |\bf x-\xi| ∣x−ξ∣ 就是 ( x , y ) (x,y) (x,y) 和 ( ξ , η ) (\xi, \eta) (ξ,η) 这两点的距离， ξ \bf{\xi} ξ 是点源位置， Γ ( x ; ξ ) \Gamma(\bf{x};\bf{\xi}) Γ(x;ξ) 代表 x \bf{x} x 处的受到的影响值。
拉普拉斯方程描述了，例如稳态温度分布、势场分布等。
泊松方程的解决了平衡情况下的场问题，比如静电场和稳态热传导等。
Green 函数和基本解的关系
格林函数通常是针对特定的边界条件定制的基本解，而基本解是更一般的数学表达，用于描述无边界条件下点源在空间中的影响。
基本解通常是针对拉普拉斯方程而言的，而格林函数则是根据具体的泊松方程和边界条件来定义的：
基本解
- 基本解 主要用于描述拉普拉斯方程 Δ u = 0 \Delta u = 0 Δu=0 在无限域或无边界条件下的解的性质。它反映了在点源作用下场的基本响应，例如，二维空间中拉普拉斯方程的基本解是 1 2 π ln 1 ∣ x − ξ ∣ \frac{1}{2\pi} \ln \frac{1}{|\mathbf{x} - \mathbf{\xi}|} 2π1ln∣x−ξ∣1。这种解决方案描述了一个理想化情况，即没有物理边界限制的空间中的场分布。
格林函数
- 格林函数 则是针对具有特定边界条件的泊松方程 Δ u = f \Delta u = f Δu=f 的解决方案。格林函数不仅包括了基本解的特性，还考虑了如何满足边界上的具体约束。格林函数确保了整个方程的解在边界上满足例如Dirichlet或Neumann边界条件。这使得格林函数成为一个更通用且实用的工具，适用于具有实际物理边界的问题。
边界条件的影响
- 格林函数的具体形式依赖于边界条件的类型。例如，在Dirichlet问题中，格林函数在边界上必须为零，以保证解在边界上的值符合规定。在Neumann问题中，格林函数在边界上的导数（即法向导数）应该符合边界上的
求 Green 函数 *
二维空间 Dirichlet \text{Dirichlet} Dirichlet 边界条件下的泊松方程：
{ − Δ u = f ( x , y ) , ( x , y ) ∈ Ω u ∣ ∂ Ω = φ \left\{ \begin{array}{l} -\Delta u = f(x,y),\ (x,y)\in\Omega \\ u|_{\partial\Omega} = \varphi \end{array} \right. {−Δu=f(x,y), (x,y)∈Ωu∣∂Ω=φ
Poission \text{Poission} Poission 方程 Dirichlet \text{Dirichlet} Dirichlet 问题的解中的格林函数 G G G 满足
{ − Δ ( x , y ) G ( x , y ; ξ , η ) = δ ( x − ξ , y − η ) , G ( x , y ; ξ , η ) ∣ ∂ Ω = 0 \left\{ \begin{array}{l} -\Delta_{(x,y)} G(x, y; \xi, \eta) = \delta(x - \xi, y - \eta), \\ \\ G(x, y; \xi, \eta)|_{\partial\Omega} = 0 \end{array} \right. ⎩ ⎨ ⎧−Δ(x,y)G(x,y;ξ,η)=δ(x−ξ,y−η),G(x,y;ξ,η)∣∂Ω=0
为什么满足这两个条件？
泊松方程的 Dirichlet \text{Dirichlet} Dirichlet 问题，其解中所使用的格林函数 G ( x , y ; ξ , η ) G(x, y; \xi, \eta) G(x,y;ξ,η) 需要满足一组特定的要求，以保证解的正确性并且满足边界条件。这些要求体现在格林函数的定义和边界条件上，对应于泊松方程解决特定边界值问题的需求。
1. 拉普拉斯算子作用于格林函数等于狄拉克δ函数
在数学上，格林函数 G ( x , y ; ξ , η ) G(x, y; \xi, \eta) G(x,y;ξ,η) 定义为： − Δ ( x , y ) G ( x , y ; ξ , η ) = δ ( x − ξ , y − η ) -\Delta_{(x,y)} G(x, y; \xi, \eta) = \delta(x - \xi, y - \eta) −Δ(x,y)G(x,y;ξ,η)=δ(x−ξ,y−η)这里的 Δ ( x , y ) \Delta_{(x,y)} Δ(x,y) 表示对 ( x , y ) (x, y) (x,y) 使用拉普拉斯算子，而 δ ( x − ξ , y − η ) \delta(x - \xi, y - \eta) δ(x−ξ,y−η) 表示在点 ( ξ , η ) (\xi, \eta) (ξ,η) 处的点源，是二维Dirac δ函数，。
此性质说明格林函数是拉普拉斯方程的基本解，它表示在源点 ( ξ , η ) (\xi, \eta) (ξ,η) 处的影响如何传播到 ( x , y ) (x, y) (x,y) 点。此设置使得格林函数能够用来构建泊松方程的解，通过将源函数 f ( x , y ) f(x, y) f(x,y) 与格林函数卷积（积分）来表达影响的累积效果。
2. 格林函数在边界上的值为零
格林函数满足的边界条件是： G ( x , y ; ξ , η ) ∣ ∂ Ω = 0 G(x, y; \xi, \eta)|_{\partial\Omega} = 0 G(x,y;ξ,η)∣∂Ω=0
这意味着，当点 ( x , y ) (x, y) (x,y) 在域 Ω \Omega Ω 的边界 ∂ Ω \partial\Omega ∂Ω 上时，格林函数的值为零。
这一条件的设置是为了保证用格林函数表示的解满足 Dirichlet \text{Dirichlet} Dirichlet 边界条件，即使得问题的解在边界上取特定的已知值（在本问题中，这个值是0）。格林函数在边界上为零确保了任何通过格林函数构建的解自动满足边界上的 Dirichlet \text{Dirichlet} Dirichlet 条件，因此解 u ( x , y ) u(x, y) u(x,y) 可以独立于边界值问题的特定形式被正确地构建。
第一象限
泊松方程 Dirichlet 边界条件
{ − Δ u = f ( x , y ) , ( x , y ) ∈ Ω u ∣ ∂ Ω = φ \left\{ \begin{array}{l} -\Delta u = f(x,y),\ (x,y)\in\Omega \\ u|_{\partial\Omega} = \varphi \end{array} \right. {−Δu=f(x,y), (x,y)∈Ωu∣∂Ω=φ
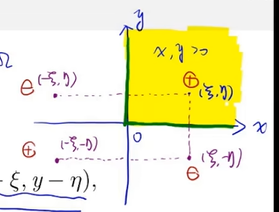
Green 函数需要满足在区域 Ω \Omega Ω 边界为 0 0 0 这里另外三个点源是虚拟的，注意圆圈里的正负号代表是热源(汇)或正(负)电荷
第四象限的负电荷保证了在 x x x 轴上为 0 0 0 ，但是它对 y y y 轴产生了作用，所以，第二象限的负电荷只能保证如果没有第四象限的负电荷情况下 在 y y y 轴上为 0 0 0，反过来，在第二象限的负电荷存在下，第四象限的负电荷也无法确保在 x x x 轴上为 0 0 0 ，这时只需要在第三象限添加一个正电荷就可以确保 x , y x,y x,y 轴都为 0 0 0
所以第一象限这种情况格林函数为 G ( x , y ; ξ , η ) = Γ ( x , y ; ξ , η ) − Γ ( x , y ; − ξ , η ) + Γ ( x , y ; − ξ , − η ) − Γ ( x , y ; ξ , − η ) G(x,y;\xi,\eta)=\Gamma(x,y;\xi,\eta)-\Gamma(x,y;-\xi,\eta)+\Gamma(x,y;-\xi,-\eta)-\Gamma(x,y;\xi,-\eta) G(x,y;ξ,η)=Γ(x,y;ξ,η)−Γ(x,y;−ξ,η)+Γ(x,y;−ξ,−η)−Γ(x,y;ξ,−η) = 1 2 π ln 1 ( x − ξ ) 2 + ( y − η ) 2 − 1 2 π ln 1 ( x + ξ ) 2 + ( y − η ) 2 =\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y-\eta)^2}}-\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x+\xi)^2+(y-\eta)^2}} =2π1ln(x−ξ)2+(y−η)21−2π1ln(x+ξ)2+(y−η)21 + 1 2 π ln 1 ( x + ξ ) 2 + ( y + η ) 2 − 1 2 π ln 1 ( x − ξ ) 2 + ( y + η ) 2 +\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x+\xi)^2+(y+\eta)^2}}-\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y+\eta)^2}} +2π1ln(x+ξ)2+(y+η)21−2π1ln(x−ξ)2+(y+η)21 这里等式右端每项的正负号和其电荷正负性相对应
Neumann 边界条件
往年真题 { − Δ u = f ( x , y ) , ( x , y ) ∈ Ω ∂ u ∂ n ∣ ∂ Ω = φ \left\{ \begin{array}{l} -\Delta u = f(x,y),\ (x,y)\in\Omega \\ \frac{\partial u}{\partial n}|_{\partial\Omega} = \varphi \end{array} \right. {−Δu=f(x,y), (x,y)∈Ω∂n∂u∣∂Ω=φ其中 Ω = { ( x , y ) ∣ x > 0 , y > 0 } \Omega =\{(x,y)|x>0,y>0\} Ω={(x,y)∣x>0,y>0}，即第一象限，用镜像法求 Green 函数，
基本解 Γ ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 + ( y − η ) 2 \Gamma(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y-\eta)^2}} Γ(x,y;ξ,η)=2π1ln(x−ξ)2+(y−η)21
画出对应的虚拟点源位置如下图
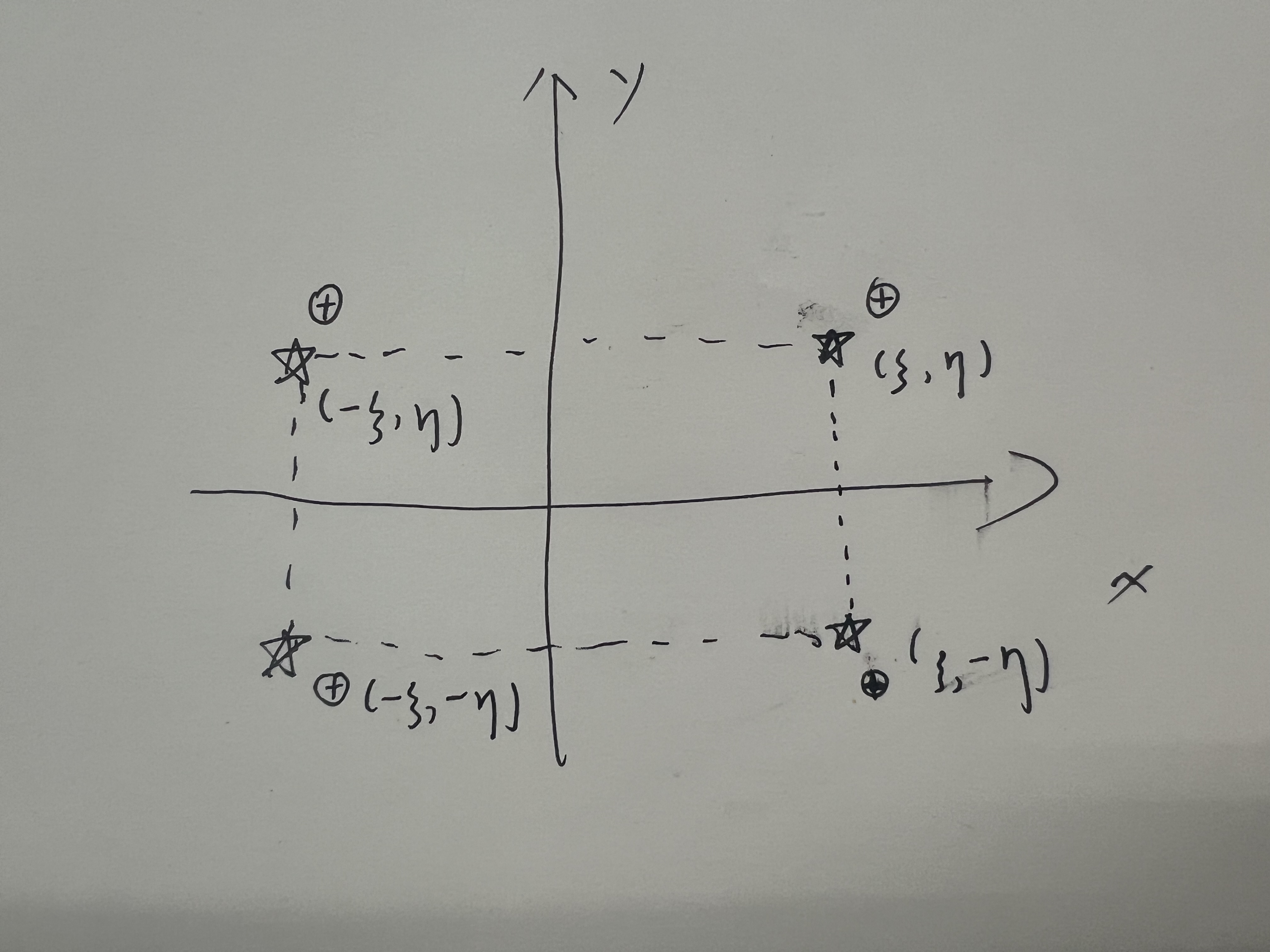这里不同的是虚拟电源的正负号，我的理解是在第一象限边界上 u u u 对外法向量求导是 0 0 0, 即温度(电场强度) 在区域边界上是恒定的常值，变化率为 0 0 0，那么可以写出格林函数表达式为 G ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 + ( y − η ) 2 + 1 2 π ln 1 ( x + ξ ) 2 + ( y − η ) 2 G(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y-\eta)^2}}+\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x+\xi)^2+(y-\eta)^2}} G(x,y;ξ,η)=2π1ln(x−ξ)2+(y−η)21+2π1ln(x+ξ)2+(y−η)21 + 1 2 π ln 1 ( x + ξ ) 2 + ( y + η ) 2 + 1 2 π ln 1 ( x − ξ ) 2 + ( y + η ) 2 +\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x+\xi)^2+(y+\eta)^2}}+\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y+\eta)^2}} +2π1ln(x+ξ)2+(y+η)21+2π1ln(x−ξ)2+(y+η)21
全圆区域
什么是反演点？
在数学中，特别是在几何学中，反演点是指通过圆反演变换后得到的点。圆反演是一种几何变换，它将平面上的点映射到另一个点，这个映射是关于一个给定的圆进行的。给定一个圆，称为反演圆，具有中心 O O O 和半径 r r r，对于平面上的任意点 P P P（不是 O O O），其反演点 P ′ P' P′ 定义如下：
- P ′ P' P′ 位于射线 O P OP OP 上。
- O P × O P ′ = r 2 OP \times OP' = r^2 OP×OP′=r2，即 P P P 和 P ′ P' P′ 关于反演圆的半径的乘积等于反演圆半径的平方。
因此，如果点 P P P 在反演圆内部，则它的反演点 P ′ P' P′ 在反演圆外部，反之亦然。如果点 P P P 在反演圆上，则它是自身的反演点。这种反演变换在复数平面上也有对应的表述，并且在解决某些几何问题时非常有用。
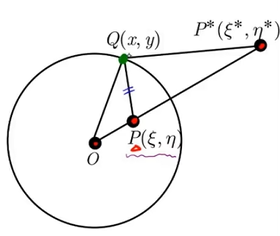
Dirichlet 边界条件
对全圆区域内的点 P ( ξ , η ) P(\xi,\eta) P(ξ,η) 在区域外取其反演点 P ∗ ( ξ ∗ , η ∗ ) P^*(\xi^*,\eta^*) P∗(ξ∗,η∗)，如果圆的半径为 a a a，那么格林函数为 G ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 + ( y − η ) 2 − 1 2 π ln a ρ ( x − ξ ∗ ) 2 + ( y − η ∗ ) 2 G(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y-\eta)^2}}-\frac{1}{2\pi}\ln\frac{\frac{a}{\rho}}{\sqrt{(x-\xi^*)^2+(y-\eta^*)^2}} G(x,y;ξ,η)=2π1ln(x−ξ)2+(y−η)21−2π1ln(x−ξ∗)2+(y−η∗)2ρa这里右端两项的正负号也是和正负电荷 (或热源热汇) 对应
如果记 Γ ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 − ( y − η ) 2 , Γ ∗ ( x , y ; ξ ∗ , η ∗ ) = 1 2 π ln a ρ ( x − ξ ∗ ) 2 − ( y − η ∗ ) 2 \Gamma(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2-(y-\eta)^2}},\Gamma^{*}(x,y;\xi^{*},\eta^{*})=\frac{1}{2\pi}\ln\frac{\frac{a}{\rho}}{\sqrt{(x-\xi^{*})^2-(y-\eta^{*})^2}} Γ(x,y;ξ,η)=2π1ln(x−ξ)2−(y−η)21,Γ∗(x,y;ξ∗,η∗)=2π1ln(x−ξ∗)2−(y−η∗)2ρa
那么上式可写为 G ( x , y ; ξ , η ) = Γ ( x , y ; ξ , η ) − Γ ∗ ( x , y ; ξ ∗ , η ∗ ) G(x,y;\xi,\eta)=\Gamma(x,y;\xi,\eta)-\Gamma^{*}(x,y;\xi^{*},\eta^{*}) G(x,y;ξ,η)=Γ(x,y;ξ,η)−Γ∗(x,y;ξ∗,η∗)
半圆区域
Dirichlet 边界条件
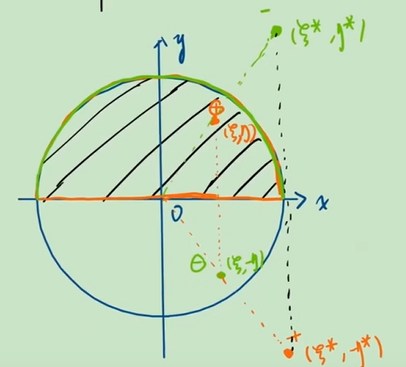
Ω \Omega Ω 是上半平面的半圆，那么它有 x x x 轴边界和半圆弧边界， ( ξ , − η ) (\xi,-\eta) (ξ,−η) 处的虚拟点源确保了 x x x 轴边界为 0 0 0， ( ξ ∗ , η ∗ ) (\xi^*,\eta^*) (ξ∗,η∗) 处的是对半圆进行延拓成全圆后，利用全圆反演点取的，那么由于引入了 ( ξ ∗ , η ∗ ) (\xi^*,\eta^*) (ξ∗,η∗) 处的点源，所以需要在 ( ξ ∗ , − η ∗ ) (\xi^*,-\eta^*) (ξ∗,−η∗) 处再引入点源使得 x x x 轴边界为 0 0 0，那么格林函数为 G ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 + ( y − η ) 2 − 1 2 π ln 1 ( x − ξ ) 2 + ( y + η ) 2 G(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y-\eta)^2}}-\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2+(y+\eta)^2}} G(x,y;ξ,η)=2π1ln(x−ξ)2+(y−η)21−2π1ln(x−ξ)2+(y+η)21 − 1 2 π ln a ρ ( x − ξ ∗ ) 2 + ( y − η ∗ ) 2 + 1 2 π ln a ρ ( x − ξ ∗ ) 2 + ( y + η ∗ ) 2 -\frac{1}{2\pi}\ln\frac{\frac{a}{\rho}}{\sqrt{(x-\xi^*)^2+(y-\eta^*)^2}}+\frac{1}{2\pi}\ln\frac{\frac{a}{\rho}}{\sqrt{(x-\xi^*)^2+(y+\eta^*)^2}} −2π1ln(x−ξ∗)2+(y−η∗)2ρa+2π1ln(x−ξ∗)2+(y+η∗)2ρa这里注意两个反演点的关于 ln \ln ln 的表达式中，分子是 a ρ \frac{a}{\rho} ρa 而不是 1 1 1
1 / 4 1/4 1/4 圆区域
Dirichlet 边界条件
二维区域 Ω = { ( x , y ) ∣ x > 0 , y > 0 , x 2 + y 2 < a 2 } \Omega=\{(x,y)|x>0,y>0,x^2+y^2<a^2\} Ω={(x,y)∣x>0,y>0,x2+y2<a2}，偏微分方程的边界条件为
{ − Δ u = f , in Ω u ∣ ∂ Ω = φ \begin{cases} -\Delta u =f,\ \text{in} \ \Omega \\ u|_{\partial\Omega}=\varphi \end{cases} {−Δu=f, in Ωu∣∂Ω=φ
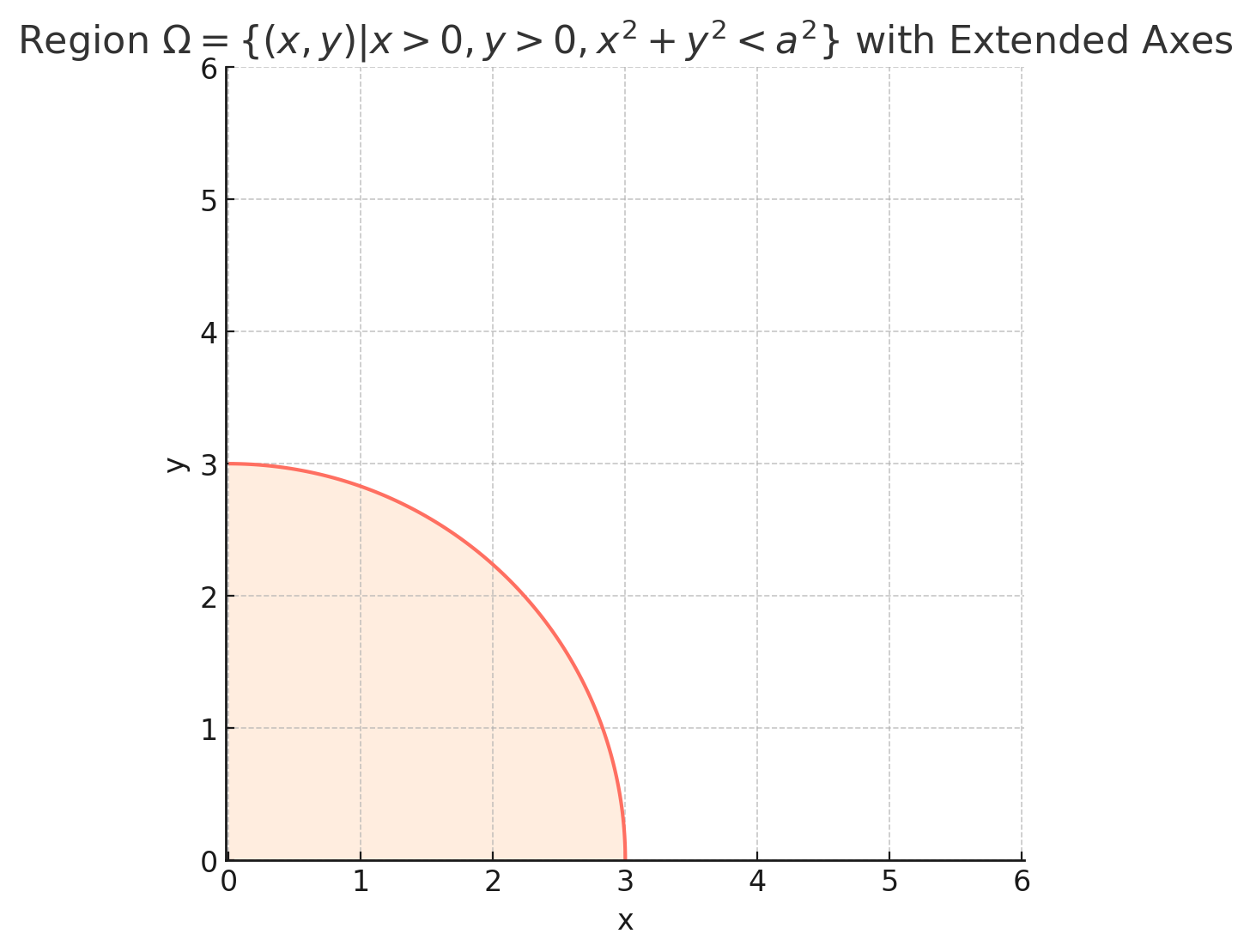
Γ ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 − ( y − η ) 2 , Γ ∗ ( x , y ; ξ ∗ , η ∗ ) = 1 2 π ln a ρ ( x − ξ ∗ ) 2 − ( y − η ∗ ) 2 \Gamma(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2-(y-\eta)^2}},\ \Gamma^{*}(x,y;\xi^{*},\eta^{*})=\frac{1}{2\pi}\ln\frac{\frac{a}{\rho}}{\sqrt{(x-\xi^{*})^2-(y-\eta^{*})^2}} Γ(x,y;ξ,η)=2π1ln(x−ξ)2−(y−η)21, Γ∗(x,y;ξ∗,η∗)=2π1ln(x−ξ∗)2−(y−η∗)2ρa请求解Green函数用 Γ ( x , y ; ξ , η ) \Gamma(x,y;\xi,\eta) Γ(x,y;ξ,η)和 Γ ∗ ( x , y ; ξ ∗ , η ∗ ) \Gamma^{*}(x,y;\xi^{*},\eta^{*}) Γ∗(x,y;ξ∗,η∗)表示的表达式
画出对应的虚拟点源位置如下图
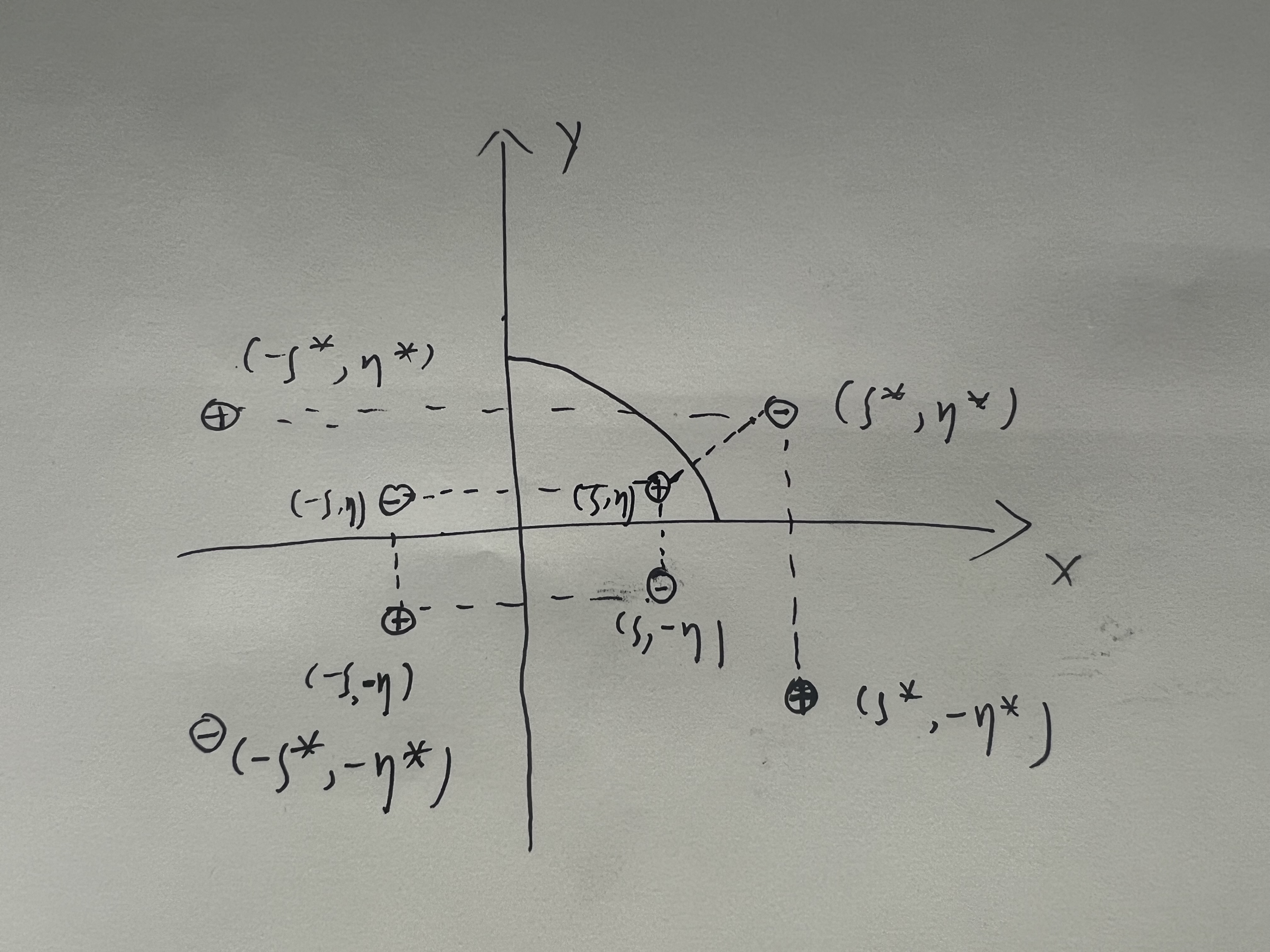
( − ξ , η ) , ( − ξ , − η ) , ( ξ , − η ) (-\xi,\eta),(-\xi,-\eta),(\xi,-\eta) (−ξ,η),(−ξ,−η),(ξ,−η) 三处的虚拟电源确保了在 x , y x,y x,y 轴边界为 0 0 0, 那么对于 1 / 4 1/4 1/4 圆弧需要在 ( ξ ∗ , η ∗ ) (\xi^*,\eta^*) (ξ∗,η∗) 处引入反演点，由于该反演点的引入，所以又需要引入其他三个点 ( − ξ ∗ , η ∗ ) , ( ξ ∗ , − η ∗ ) , ( − ξ ∗ , − η ∗ ) (-\xi^*,\eta^*),(\xi^*,-\eta^*),(-\xi^*,-\eta^*) (−ξ∗,η∗),(ξ∗,−η∗),(−ξ∗,−η∗) 确保 x , y x,y x,y 轴边界为 0 0 0，
Γ ( x , y ; ξ , η ) = 1 2 π ln 1 ( x − ξ ) 2 − ( y − η ) 2 , Γ ∗ ( x , y ; ξ ∗ , η ∗ ) = 1 2 π ln a ρ ( x − ξ ∗ ) 2 − ( y − η ∗ ) 2 \Gamma(x,y;\xi,\eta)=\frac{1}{2\pi}\ln\frac{1}{\sqrt{(x-\xi)^2-(y-\eta)^2}},\ \Gamma^{*}(x,y;\xi^{*},\eta^{*})=\frac{1}{2\pi}\ln\frac{\frac{a}{\rho}}{\sqrt{(x-\xi^{*})^2-(y-\eta^{*})^2}} Γ(x,y;ξ,η)=2π1ln(x−ξ)2−(y−η)21, Γ∗(x,y;ξ∗,η∗)=2π1ln(x−ξ∗)2−(y−η∗)2ρa
那么格林函数为 G ( x , y ; ξ , η ) = Γ ( x , y ; ξ , η ) − Γ ( x , y ; − ξ , η ) − Γ ( x , y ; ξ , − η ) − Γ ( x , y ; ξ , − η ) G(x,y;\xi,\eta)=\Gamma(x,y;\xi,\eta)-\Gamma(x,y;-\xi,\eta)-\Gamma(x,y;\xi,-\eta)-\Gamma(x,y;\xi,-\eta) G(x,y;ξ,η)=Γ(x,y;ξ,η)−Γ(x,y;−ξ,η)−Γ(x,y;ξ,−η)−Γ(x,y;ξ,−η) − Γ ∗ ( x , y ; ξ ∗ , η ∗ ) + Γ ∗ ( x , y ; − ξ ∗ , η ∗ ) + Γ ∗ ( x , y ; ξ ∗ , − η ∗ ) − Γ ∗ ( x , y ; − ξ ∗ , − η ∗ ) -\Gamma^*(x,y;\xi^*,\eta^*)+\Gamma^*(x,y;-\xi^*,\eta^*)+\Gamma^*(x,y;\xi^*,-\eta^*)-\Gamma^*(x,y;-\xi^*,-\eta^*) −Γ∗(x,y;ξ∗,η∗)+Γ∗(x,y;−ξ∗,η∗)+Γ∗(x,y;ξ∗,−η∗)−Γ∗(x,y;−ξ∗,−η∗)
Neumann 边界条件结合 Dirichlet 边界条件
{ − Δ u = f , in Ω u ∣ ∂ Ω ∩ ∂ B a = φ ∂ u ∂ n ∣ { x = 0 或 y = 0 } ∩ ∂ Ω = ψ \begin{cases} -\Delta u =f,\ \text{in} \ \Omega \\ u|_{\partial\Omega\cap\partial B_a}=\varphi \\ \frac{\partial u}{\partial n}|_{\{x=0或y=0\}\cap \partial\Omega}=\psi \end{cases} ⎩ ⎨ ⎧−Δu=f, in Ωu∣∂Ω∩∂Ba=φ∂n∂u∣{x=0或y=0}∩∂Ω=ψ也就是在 1 / 4 1/4 1/4 圆弧上满足 Dirichlet 边界条件, 在 x , y x,y x,y 坐标轴上的边界满足 Neumann 边界条件
画出对应的虚拟点源位置如下图
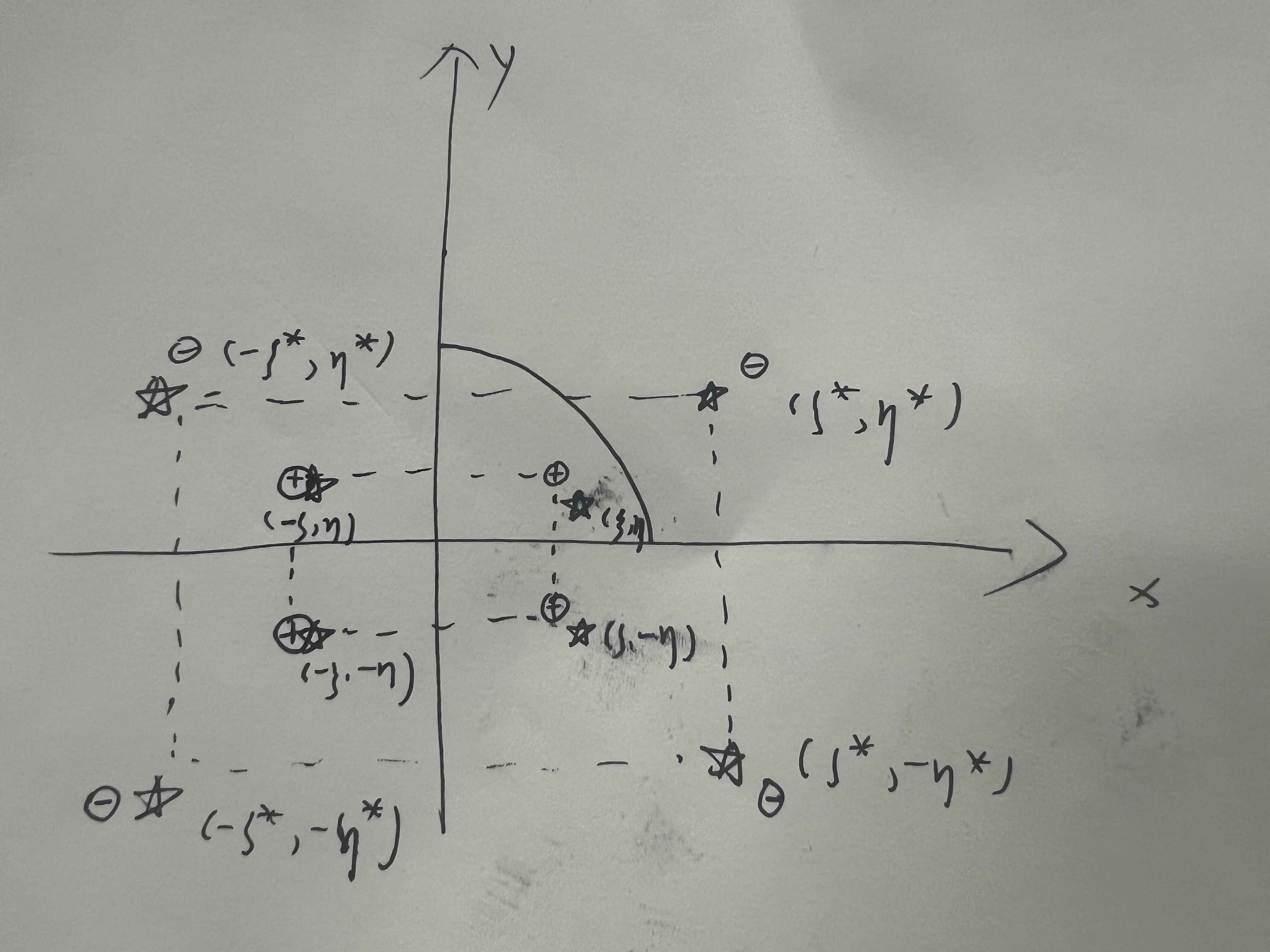
同理 ( − ξ , η ) , ( − ξ , − η ) , ( ξ , − η ) (-\xi,\eta),(-\xi,-\eta),(\xi,-\eta) (−ξ,η),(−ξ,−η),(ξ,−η) 三处的虚拟电源确保了在 x , y x,y x,y 轴边界 u u u 对外法向量导数为 0 0 0，那么对于 1 / 4 1/4 1/4 圆弧需要在 ( ξ ∗ , η ∗ ) (\xi^*,\eta^*) (ξ∗,η∗) 处引入反演点，由于该反演点的引入，所以又需要引入其他三个点 ( − ξ ∗ , η ∗ ) , ( ξ ∗ , − η ∗ ) , ( − ξ ∗ , − η ∗ ) (-\xi^*,\eta^*),(\xi^*,-\eta^*),(-\xi^*,-\eta^*) (−ξ∗,η∗),(ξ∗,−η∗),(−ξ∗,−η∗) 确保在 x , y x,y x,y 轴边界 u u u 对外法向量导数为 0 0 0，所以格林函数可以写成 G ( x , y ; ξ , η ) = Γ ( x , y ; ξ , η ) + Γ ( x , y ; − ξ , η ) + Γ ( x , y ; ξ , − η ) + Γ ( x , y ; ξ , − η ) G(x,y;\xi,\eta)=\Gamma(x,y;\xi,\eta)+\Gamma(x,y;-\xi,\eta)+\Gamma(x,y;\xi,-\eta)+\Gamma(x,y;\xi,-\eta) G(x,y;ξ,η)=Γ(x,y;ξ,η)+Γ(x,y;−ξ,η)+Γ(x,y;ξ,−η)+Γ(x,y;ξ,−η) − Γ ∗ ( x , y ; ξ ∗ , η ∗ ) − Γ ∗ ( x , y ; − ξ ∗ , η ∗ ) − Γ ∗ ( x , y ; ξ ∗ , − η ∗ ) − Γ ∗ ( x , y ; − ξ ∗ , − η ∗ ) -\Gamma^*(x,y;\xi^*,\eta^*)-\Gamma^*(x,y;-\xi^*,\eta^*)-\Gamma^*(x,y;\xi^*,-\eta^*)-\Gamma^*(x,y;-\xi^*,-\eta^*) −Γ∗(x,y;ξ∗,η∗)−Γ∗(x,y;−ξ∗,η∗)−Γ∗(x,y;ξ∗,−η∗)−Γ∗(x,y;−ξ∗,−η∗)
这篇关于PDE求格林函数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
