本文主要是介绍PDE-GCN:偏微分方程下的图卷积神经网络,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
NeurIPS 2021文献: PDE-GCN: Novel Architectures for Graph Neural
Networks Motivated by Partial Differential Equations
图形神经网络正日益成为各种领域的主流方法计算机视觉、计算生物学和化学等领域的数据这些都可以用图表自然地解释。然而,与传统的卷积神经网络不同网络,深图网络不一定比其他网络产生更好的性能浅图网络。这种行为通常源于过度平滑现象在这项工作中,我们提出了一系列体系结构来控制这一点设计的行为。我们的网络是由数值方法驱动的流形上的偏微分方程(PDE),因此,它们的行为可以可以用类似的分析来解释。此外,正如我们使用广泛的通过一系列实验,我们的PDE激励网络可以推广并有效针对不同领域的各种类型的问题。我们的架构获得了更好的性能或者与当前典型的问题的最新结果相符合使用不同的体系结构。

扩散过程:
两个方程–非线性扩散方程和非线性双曲方程
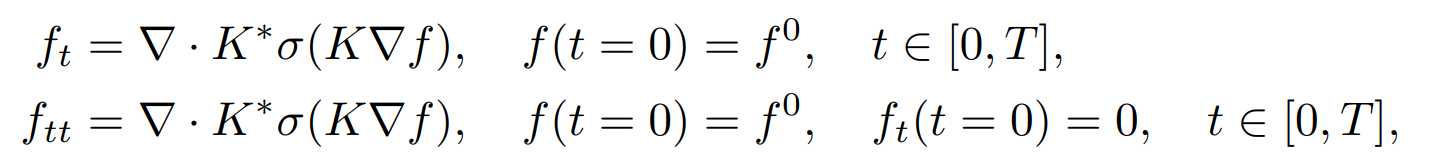
将微分方程离散化,可得到如下的方程:
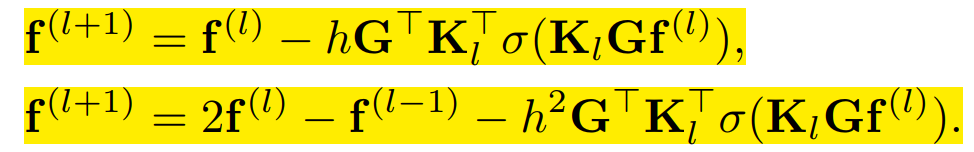
迭代过程就是图神经网络的训练过程。
图上的梯度算子可以离散化为
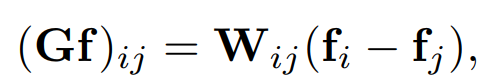
实验:




这篇关于PDE-GCN:偏微分方程下的图卷积神经网络的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









